rút gọn
ab-bd-be+ce+cd+ae
NT
Những câu hỏi liên quan
Cho tam giác ABC . Gọi M là trung điểm của BC . Quá B và C lần lượt kẻ BD và CE vuông góc với đường thẳng AM a. Chứng minh BD= CE và BD // CE b. Chứng minh BE // CD và BE = CD c. Chứng minh AD + AE = 2AM
a: Xét ΔBMD vuông tại D và ΔCME vuông tại E có
MB=MC
\(\widehat{BMD}=\widehat{CME}\)(hai góc đối đỉnh)
Do đó: ΔBMD=ΔCME
=>BD=CE
Ta có: BD\(\perp\)AM
CE\(\perp\)AM
Do đó: BD//CE
b: Xét tứ giác BDCE có
BD//CE
BD=CE
Do đó: BDCE là hình bình hành
=>BE//CD và BE=CD
c: \(AD+AE=AD+AD+DE\)
\(=2AD+2DM\)
\(=2\left(AD+DM\right)=2AM\)
Đúng 1
Bình luận (1)
đặt thừa số chung rồi đơn giản biểu thức: ab-bd-be+ce+cd+ae
ab - bd - be + ce + cd + ae = (ab - be) - (bd - cd) + (ce + ae)
= b(a - e) - d(b - c) + e(c + a)
Xem lại đề nhé, hơi căng :))
Đúng 0
Bình luận (0)
Sử dụng tính chất phân phối và kết hợp viết tổng sau thành tich :
B = ad + be + cd - ae - bd - ce
1. Cho sáu điểm A,B,C,D,E,F. Chứng minh :
a) AB+BC+CD+DA=0
b) AB+DC+BD+CA=0
c) CD+BC+AB=AD
d) AB+CD=AD+CB
e) AD+BE+CF=AE+BF+CD=AF+BD+CE
Cho 6điểm A,B,C,D,E,F .CMR
A, vector AD + vector BE + vectơ CF = vector AE+ Vectơ BF+ Vectơ CD = vector AF + VECTO BD + vectơ CE
CHo tam giác ABC nhọn có 3 đường cao là : AD , BE , CF cắt nhau tại H . Chứng minh : AE*BF*CD = AF * BD*CE=DE*EF*FD
Cho hình thang ABCD có CD=3AB .Trên CD lấy E,F sao cho CE=EF =FD. Chứng minh
a, ABFD là hình bình hành
b, AF//BE
c,AE=BC
d, Gọi M,N,P lần lượt là trung điểm của AF và BD ,AE và PF, AC và BE .Chứng minh M,N,P thẳng hàng
a) Ta có: DF=FE=CE(gt)
mà DF+FE+CE=DC
nên \(DF=FE=CE=\dfrac{DC}{3}\)
Xét tứ giác ABFD có
AB//FD(gt)
AB=FD
Do đó: ABFD là hình bình hành(Dấu hiệu nhận biết hình bình hành)
b) Xét tứ giác ABEF có
AB//EF(gt)
AB=EF(cmt)
Do đó: ABEF là hình bình hành(Dấu hiệu nhận biết hình bình hành)
Suy ra: AF=BE(Hai cạnh đối)
Đúng 1
Bình luận (0)
c) Xét tứ giác ABCE có
AB//CE
AB=CE
Do đó: ABCE là hình bình hành
Suy ra: AE=BC
Đúng 0
Bình luận (0)
Cho tam giác ABC, các đường cao BD và CE cắt nhau tại H, chứng minh :
a) AE x AB = AD x AC
b) Góc AED = góc ACB
c) Tính diện tích tam giác ABC biết AC = 6cm ; BC = 5cm ; CD = 3cm
d) BE x BA + CD x CA = BC2
a: Xet ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng vơi ΔAEC
=>AD/AE=AB/AC
=>AD*AC=AE*AB; AD/AB=AE/AC
b: Xét ΔADE và ΔABC có
AD/AB=AE/AC
góc DAE chung
=>ΔADE đồng dạng với ΔABC
c: \(DB=\sqrt{5^2-3^2}=4\left(cm\right)\)
\(S_{BAC}=\dfrac{1}{2}\cdot4\cdot6=12\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Trong Hình 76, cho biết các tam giác ABD và BCE là tam giác đều và A, B, C thẳng hàng. Chứng minh rằng:
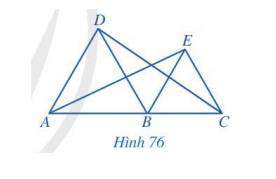
a) AD // BE và BD // CE;
b) \(\widehat {ABE} = \widehat {DBC} = 120^\circ \);
c) AE = CD.
a)
Tam giác ABD và BCE là tam giác đều nên \(\widehat {EBC} = \widehat {DAB} = 60^\circ \) và A, B, C thẳng hàng. Hai góc EBC và DAB ở vị trí đồng vị nên AD // BE.
Tam giác ABD và BCE là tam giác đều nên \(\widehat {DBA} = \widehat {ECB} = 60^\circ \) và A, B, C thẳng hàng. Hai góc DBA và ECB ở vị trí đồng vị nên BD // CE.
b) Ta có A, B, C thẳng hàng nên góc ABC bằng 180°. Mà \(\widehat {DBA} = \widehat {EBC} = 60^\circ \Rightarrow \widehat {DBE} = 60^\circ \).
Vậy \(\widehat {ABE} = \widehat {DBC} = 120^\circ \) (\(\widehat {ABE} = \widehat {DBA} + \widehat {DBE};\widehat {DBC} = \widehat {DBE} + \widehat {EBC}\)).
c) Tam giác ABD và BCE là tam giác đều
\(\Rightarrow AB=AD, BE=BC\)
Xét hai tam giác ABE và DBC có:
AB = DB;
\(\widehat {ABE} = \widehat {DBC} = 120^\circ \);
BE = BC.
\(\Rightarrow \Delta ABE = \Delta DBC\) (c.g.c)
Do đó, AE = DC ( 2 cạnh tương ứng).
Đúng 0
Bình luận (0)