Xét tính tăng giảm và lập bảng biến thiên của hàm số y = sin2x trên \(\left[-\dfrac{\pi}{2};\dfrac{\pi}{2}\right]\)
NS
Những câu hỏi liên quan
cho hàm số y = f(x) = \(2\sin2x\) .
a) lập bảng biến thiên của hàm số y = \(2\sin2x\) trên đoạn \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
b) vẽ đồ thị của hàm số y = \(2\sin2x\) .
cho hàm số y = f(x) = \(2\sin2x\) .
a) lập bảng biến thiên của hàm số y = \(2\sin2x\) trên đoạn \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
b) vẽ đồ thị của hàm số y = \(2\sin2x\) .
cho hàm số y = f(x) = \(2\sin2x\) .
a) lập bảng biến thiên của hàm số y = \(2\sin2x\) trên đoạn \(\left[-\frac{\pi}{2};\frac{\pi}{2}\right]\)
b) vẽ đồ thị của hàm số y = \(2\sin2x\) .
xét sự biến thiên của hàm số sau trên tập xác định của nó và lập bảng biến thiên:
a, \(y=-x^2-2x+3\)
b, \(y=\dfrac{x+1}{x-2}\)
a: TXĐ: D=R
Khi \(x\in D\Rightarrow-x\in D\)
\(f\left(-x\right)=-\left(-x\right)^2-2\cdot\left(-x\right)+3\)
\(=-x^2+2x+3\)
\(\Leftrightarrow f\left(-x\right)\ne f\left(x\right)\ne-f\left(x\right)\)
Vậy: Hàm số không chẵn không lẻ
Đúng 0
Bình luận (1)
Cho hàm số \(y=\sin2x+\cos2x+3.\) GTLN của hàm số trên\(\left[-\dfrac{\pi}{4};\dfrac{\pi}{4}\right]\) là số \(a+b\sqrt{2}.\) . Tính \(a+b\)
\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)+3\)
Do \(sin\left(2x+\dfrac{\pi}{4}\right)\le1\Rightarrow y\le3+\sqrt{2}\)
\(\Rightarrow a=3;b=1\Rightarrow a+b=\)
Đúng 1
Bình luận (0)
Xét sự biến thiên của mỗi hàm số sau trên các khoảng tương ứng:
a) y = sinx trên khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right),\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
b) y = cosx trên khoảng \(\left( { - 20\pi ; - 19\pi } \right),\left( { - 9\pi ; - 8\pi } \right)\)
a) y = sinx
- Khoảng \(\left( { - \frac{{9\pi }}{2}; - \frac{{7\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
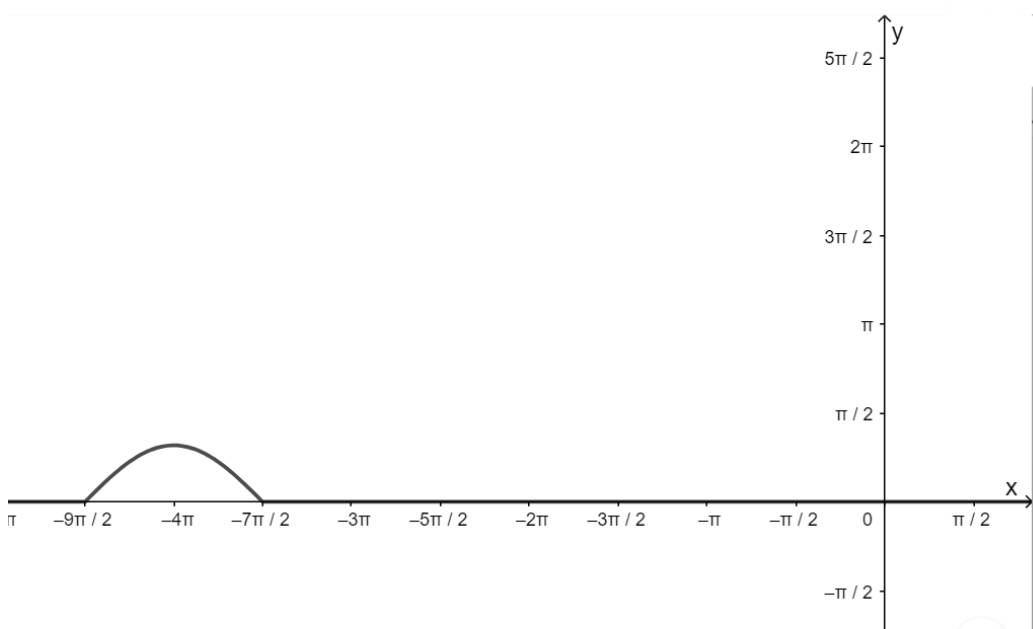
+ Đồng biến trên khoảng \(\left( { - \frac{{9\pi }}{2}; - 4\pi } \right)\)
+ Nghịch biến trên khoảng; \(\left( { - 4\pi ; - \frac{{7\pi }}{2}} \right)\)
- Khoảng \(\left( {\frac{{21\pi }}{2};\frac{{23\pi }}{2}} \right)\)
+ Vẽ đồ thị hàm số:
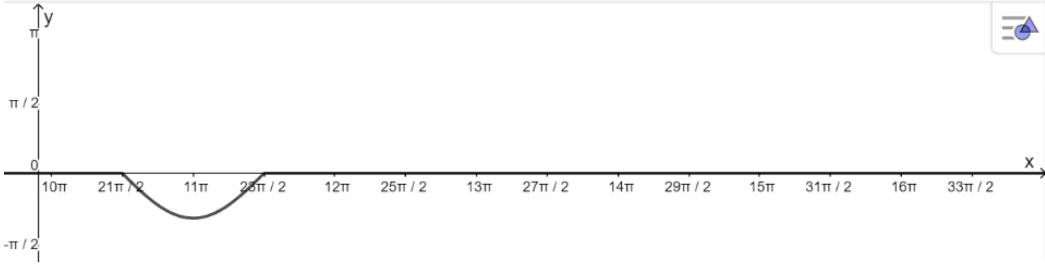
+ Đồng biến trên khoảng: \(\left( {11\pi ;\frac{{23\pi }}{2}} \right)\)
+ Nghịch biến trên khoảng: \(\left( {\frac{{21\pi }}{2};11\pi } \right)\)
Đúng 0
Bình luận (0)
xét hàm số y = f(x) = \(\sin\pi x\)
a) chứng minh rằng vưới mọi số nguyên chẵn m ta có f(x+m)=f(x) với mọi x .
b) lập bảng biến thiên của hàm số trên khoảng \(\left[-1;1\right]\)
c) vẽ đồ thị của hàm số đó
Xét tính đơn điệu của hàm số y= sinx trên \(\left(-\dfrac{\pi}{2};\dfrac{3\pi}{2}\right)\)
Cho hàm số y f(x) có bảng biến thiên như sauVà các khẳng định sau đây: (1). Hàm số đồng biến trên (-3;4) (2). Hàm số tăng trên
3
;
319
6
(3). Hàm số giảm trên
−
∞
;
−
4
∪
3
;
+...
Đọc tiếp
Cho hàm số y = f(x) có bảng biến thiên như sau
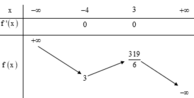
Và các khẳng định sau đây:
(1). Hàm số đồng biến trên (-3;4) (2). Hàm số tăng trên 3 ; 319 6
(3). Hàm số giảm trên − ∞ ; − 4 ∪ 3 ; + ∞ (4). Hàm số giảm trên 3 ; + ∞
Tìm số khẳng định sai trong các khẳng định trên?
A. 1
B. 2
C. 3
D. 4




