tìm điều kiện xác định để biểu thức sau có nghĩa căn của cả x+3/7-x
HT
Những câu hỏi liên quan
Tìm điều kiện xác định để các biểu thức sau có nghĩa;
a,1/1-căn x^2-3
b,x-1/2-căn 3x+1
c,2/căn x^2-x+1
d,1/căn x- căn 2x-1
\(\sqrt{\frac{3x+1}{10}}\) Tìm điều kiện xác định của x để căn thức sau có nghĩa (xác định)
Biểu thức trong căn thức \(\sqrt{\frac{3x+1}{10}}\)phải lớn hơn hoặc bằng 0
Căn thức có nghĩa\(\Leftrightarrow3x+1\ge0\Leftrightarrow x\ge\frac{-1}{3}\)
Đúng 0
Bình luận (0)
Cho biểu thức A = x căn x+1/x-1 - x -1/căn x+ 1 a,Tìm điều kiện xác định và rút gọn biểu thức A b, Tìm giá trị của biểu thức khi X = 9/4 c, Tìm tất cả giá trị của x để A
a: ĐKXĐ: x>=0; x<>1
\(A=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(=\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\)
\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{x-1}=\dfrac{x+\sqrt{x}}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
b: Khi x=9/4 thì A=3/2:1/2=3/2*2=3
Đúng 0
Bình luận (0)
tìm điều kiện của x để căn thức sau có nghĩa
căn 2020 + căn -3 phần x+3
\(\sqrt{2020}+\sqrt{-\frac{3}{x+3}}\)
Căn thức trên có nghĩa khi:\(\hept{\begin{cases}x+3\ne0\\-\frac{3}{x+3}>0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ne-3\\x+3< 0\end{cases}\Leftrightarrow\hept{\begin{cases}x\ne-3\\x< -3\end{cases}}}}\)
\(\Rightarrow x< -3\)
Tìm điều kiện xác định để biểu thức P\(=\sqrt[]{\dfrac{2023}{x+1}}\)có nghĩa
ĐKXĐ: \(x+1>0\Rightarrow x>-1\)
Đúng 1
Bình luận (0)
1. Cho biểu thức A sqrt{4-2x}a) Tìm điều kiện của x để biểu thức có nghĩa.b) Tìm giá trị của biểu thức khi x2, x0,x1,x-6,x-10.c) Tìm giá trị của biến x để giá trị của biểu thức bằng 0? Bằng 5? Bằng 10?2. Cho biểu thức P frac{9}{2sqrt{x}-3}a) Tìm điều kiện của X để biểu thức P xác định..b) Tính giá trị của biểu thức khi x4, x100c) Tìm giá trị của x để P1, P7d) Tìm các số nguyên x để giá trị của P cũng là một số nguyên.3. Cho biểu thức frac{2sqrt{x}+9}{sqrt{x}+1}a) Tìm điều kiện xác định của x để...
Đọc tiếp
1. Cho biểu thức A= \(\sqrt{4-2x}\)
a) Tìm điều kiện của x để biểu thức có nghĩa.
b) Tìm giá trị của biểu thức khi x=2, x=0,x=1,x=-6,x=-10.
c) Tìm giá trị của biến x để giá trị của biểu thức bằng 0? Bằng 5? Bằng 10?
2. Cho biểu thức P= \(\frac{9}{2\sqrt{x}-3}\)
a) Tìm điều kiện của X để biểu thức P xác định..
b) Tính giá trị của biểu thức khi x=4, x=100
c) Tìm giá trị của x để P=1, P=7
d) Tìm các số nguyên x để giá trị của P cũng là một số nguyên.
3. Cho biểu thức \(\frac{2\sqrt{x}+9}{\sqrt{x}+1}\)
a) Tìm điều kiện xác định của x để biểu thức Q được xác định.
b) Tính giá trị của biểu thức khi x=0,x=1,x=16.
c) Tìm giá trị của x để Q=1,Q=10.
d) Tìm các số nguyên x để giá trị của Q cũng là một số nguyên.
Giải hộ với ạ! Gấp lắm T.T
1) a) Căn thức có nghĩa \(\Leftrightarrow4-2x\ge0\Leftrightarrow2x\le4\Leftrightarrow x\le2\)
b) Thay x = 2 vào biểu thức A, ta được: \(A=\sqrt{4-2.2}=\sqrt{0}=0\)
Thay x = 0 vào biểu thức A, ta được: \(A=\sqrt{4-2.0}=\sqrt{4}=2\)
Thay x = 1 vào biểu thức A, ta được: \(A=\sqrt{4-2.1}=\sqrt{2}\)
Thay x = -6 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-6\right)}=\sqrt{16}=4\)
Thay x = -10 vào biểu thức A, ta được: \(A=\sqrt{4-2.\left(-10\right)}=\sqrt{24}=2\sqrt{6}\)
c) \(A=0\Leftrightarrow\sqrt{4-2x}=0\Leftrightarrow4-2x=0\Leftrightarrow x=2\)
\(A=5\Leftrightarrow\sqrt{4-2x}=5\Leftrightarrow4-2x=25\Leftrightarrow x=\frac{-21}{2}\)
\(A=10\Leftrightarrow\sqrt{4-2x}=10\Leftrightarrow4-2x=100\Leftrightarrow x=-48\)
Đúng 0
Bình luận (0)
2) a) P xác định \(\Leftrightarrow x\ge0\)và \(2\sqrt{x}-3\ne0\Leftrightarrow\sqrt{x}\ne\frac{3}{2}\Leftrightarrow x\ne\frac{9}{4}\)
b) Thay x = 4 vào P, ta được: \(P=\frac{9}{2\sqrt{4}-3}=\frac{9}{1}=9\)
Thay x = 100 vào P, ta được: \(P=\frac{9}{2\sqrt{100}-3}=\frac{9}{17}\)
c) P = 1 \(\Leftrightarrow\frac{9}{2\sqrt{x}-3}=1\Leftrightarrow2\sqrt{x}-3=9\Leftrightarrow\sqrt{x}=6\Leftrightarrow x=36\)
P = 7 \(\Leftrightarrow\frac{9}{2\sqrt{x}-3}=7\Leftrightarrow2\sqrt{x}-3=\frac{9}{7}\)
\(\Leftrightarrow2\sqrt{x}=\frac{30}{7}\Leftrightarrow\sqrt{x}=\frac{15}{7}\Leftrightarrow x=\frac{225}{49}\)
d) P nguyên \(\Leftrightarrow9⋮2\sqrt{x}-3\)
\(\Leftrightarrow2\sqrt{x}-3\inƯ\left(9\right)=\left\{\pm1;\pm3;\pm9\right\}\)
Lập bảng:
| \(2\sqrt{x}-3\) | \(1\) | \(-1\) | \(3\) | \(-3\) | \(9\) | \(-9\) |
| \(\sqrt{x}\) | \(2\) | \(1\) | \(3\) | \(0\) | \(6\) | \(-3\) |
| \(x\) | \(4\) | \(1\) | \(9\) | \(0\) | \(36\) | \(L\) |
Vậy \(x\in\left\{1;4;9;0;36\right\}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
B. Bài tập cơ bản.Bài 2.1Tìm x để mỗi căn thức sau đây có nghĩa: Bài 2.2Tìm điều kiện của x để biểu thức sau đây có nghĩa: Bài 2.3Tính: Bài 2.4Rút gọn các biểu thức sau: Bài 2.5Giải các phương trình sau:
Đọc tiếp
B. Bài tập cơ bản.
Bài 2.1
Tìm x để mỗi căn thức sau đây có nghĩa:
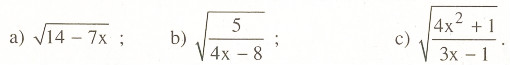
Bài 2.2
Tìm điều kiện của x để biểu thức sau đây có nghĩa:
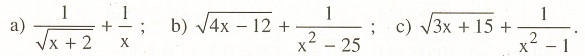
Bài 2.3
Tính:
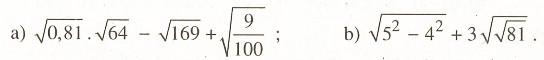
Bài 2.4
Rút gọn các biểu thức sau:
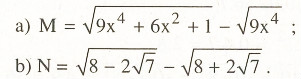
Bài 2.5
Giải các phương trình sau:
![]()
a) Căn thức có nghĩa `<=> 14-7x >=0 <=> x <= 2`
b) Căn thức có nghĩa `<=> 4x-8>0 <=> x>2`
`(5>=0 forall x)`
c) Căn thức có nghĩa `<=>3x-1 > 0 <=> x >1/3`
`(4x^2+1>0 forall x)`
Đúng 0
Bình luận (0)
a) Để \(\sqrt{14-7x}\) có nghĩa là 14 -7x ≥ 0
Ta có: 14 -7x ≥ 0
-7x ≥ -14
x ≤ 2
Vậy x ≤ 2
Đúng 0
Bình luận (0)
Tìm điều kiện xác định để biểu thức có nghĩa
\(\sqrt{x^2+2x+3}\)
5 phan 8 thanh so thap phan la bao nhieu
\(\sqrt{x^2+2x+3}=\sqrt{\left(x+1\right)^2+2}\)
Vì \(\left(x+1\right)^2\ge0\forall x\)nên \(\left(x+1\right)^2+2\ge2\forall x\)
Biểu thức trong căn luôn lớn hơn 0 nên \(\sqrt{x^2+2x+3}\)có nghĩa với mọi x thực
tìm điều kiện của x để căn thức a) \(\sqrt{x+5}\) ;b) \(\sqrt{7-x}\); c)\(\sqrt{\dfrac{1}{x+3}}\) ;d)\(\sqrt{\dfrac{-2}{x-3}}\) có nghĩa
a) ĐKXĐ: \(x+5\ge0\Leftrightarrow x\ge-5\)
b) ĐKXĐ: \(7-x\ge0\Leftrightarrow x\le7\)
c) ĐKXĐ: \(x+3>0\Leftrightarrow x>-3\)
d) ĐKXĐ: \(x-3< 0\Leftrightarrow x< 3\)
Đúng 0
Bình luận (0)




