Giúp mình mấy bài này với mọi ngừi ơi
TH
Những câu hỏi liên quan
Mọi ngừi ơi giúp mình mấy bài này với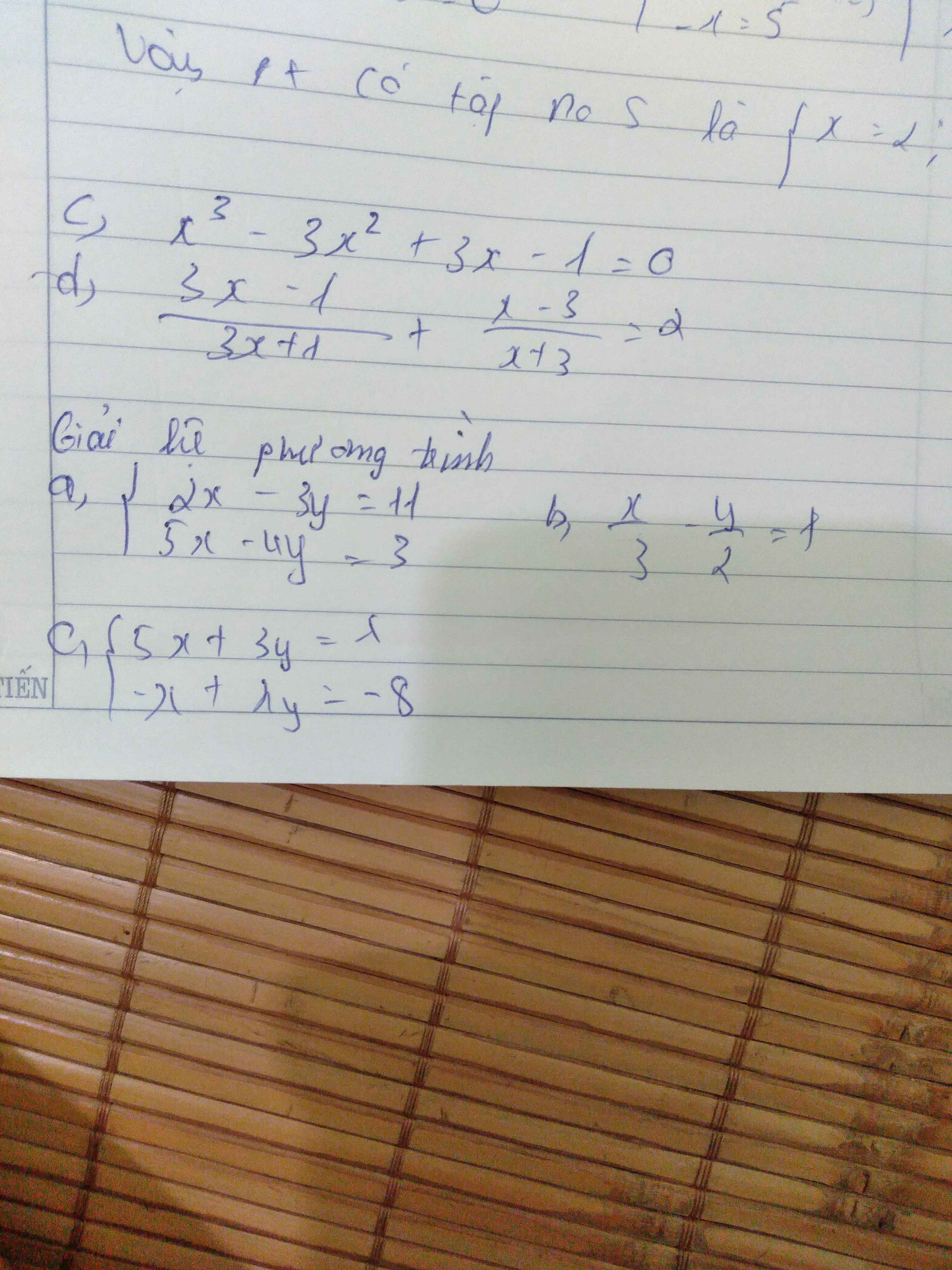
Lời giải.
c.
$x^3-3x^2+3x-1=0$
$\Leftrightarrow (x-1)^3=0$
$\Leftrightarrow x-1=0$
$\Leftrightarrow x=1$
Vậy pt có tập nghiệm $S=\left\{1\right\}$
d. ĐKXĐ: $x\neq \frac{-1}{3}; -3$
PT $\Leftrightarrow \frac{(3x-1)(x+3)+(x-3)(3x+1)}{(3x+1)(x+3)}=2$
$\Leftrightarrow \frac{6x^2-6}{3x^2+10x+3}=2$
$\Leftrightarrow 6x^2-6=2(3x^2+10x+3)$
$\Leftrightarrow 20x+12=0$
$\Leftrightarrow x=\frac{-3}{5}$ (tm)
Vậy tập nghiệm của pt là $S=\left\{\frac{-3}{5}\right\}$
Đúng 0
Bình luận (0)
Bài 2:
a.
\(\left\{\begin{matrix} 2x-3y=11\\ 5x-4y=3\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 10x-15y=55\\ 10x-8y=6\end{matrix}\right.\)
\(\Rightarrow (10x-8y)-(10x-15y)=6-55\)
\(\Leftrightarrow 7y=-49\Leftrightarrow y=-7\)
\(x=\frac{3y+11}{2}=\frac{3.(-7)+11}{2}=-5\)
Vậy hpt có nghiệm $(x,y)=(-5,-7)$
b. Không đủ cơ sở để tìm $x,y$
c.
\(\left\{\begin{matrix} 5x+3y=\lambda\\ -x+\lambda y=-8\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} 5x+3y=\lambda\\ -5x+5\lambda y=-40\end{matrix}\right.\)
\(\Rightarrow (3+5\lambda)y=\lambda-40\)
Nếu $\lambda = \frac{-3}{5}$ thì $0.y=\frac{-203}{5}$ (vô lý) nên hpt vô nghiệm
Nếu $\lambda \neq \frac{-3}{5}$ thì:
$y=\frac{\lambda - 40}{3+5\lambda}$
$x=8+\lambda y=\frac{\lambda ^2+24}{5\lambda +3}$
Đúng 1
Bình luận (2)
Giúp mình bài này với mọi ngừi ơi. 😭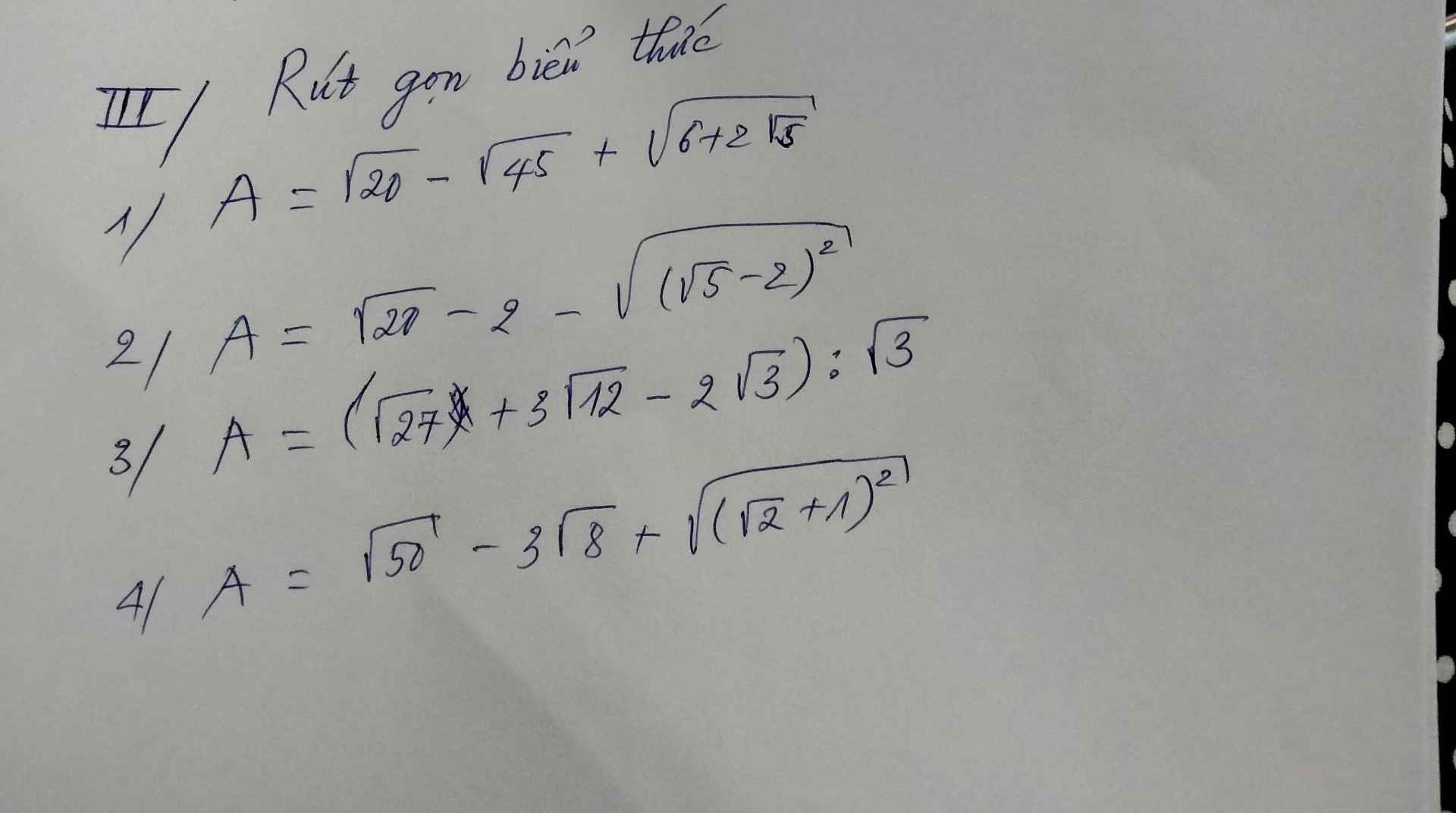
\(\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}=\sqrt{2^2.5}-\sqrt{3^2.5}+\sqrt{\left(\sqrt{5}+1\right)^2}=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1=1\)
\(\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}=2\sqrt{5}-2-\left|\sqrt{5}-2\right|=2\sqrt{5}-2-\sqrt{5}+2=\sqrt{5}\)
\(\left(\sqrt{27}+3\sqrt{12}-2\sqrt{3}\right):\sqrt{3}=\left(3\sqrt{3}+6\sqrt{3}-2\sqrt{3}\right):\sqrt{3}=7\sqrt{3}:\sqrt{3}=7\)
\(\sqrt{50}-3\sqrt{8}+\sqrt{\left(\sqrt{2}+1\right)^2}=\sqrt{5^2.2}-3\sqrt{2^2.2}+\sqrt{\left(\sqrt{2}+1\right)^2}=5\sqrt{2}-6\sqrt{2}+\sqrt{2}+1=1\)
Đúng 0
Bình luận (0)
1) \(A=\sqrt{20}-\sqrt{45}+\sqrt{6+2\sqrt{5}}\)
\(=2\sqrt{5}-3\sqrt{5}+\sqrt{5}+1\)
=1
2) Ta có: \(B=\sqrt{20}-2-\sqrt{\left(\sqrt{5}-2\right)^2}\)
\(=2\sqrt{5}-2-\sqrt{5}+2\)
\(=\sqrt{5}\)
Đúng 0
Bình luận (0)
3) Ta có: \(\left(\sqrt{27}+3\sqrt{12}-2\sqrt{3}\right):\sqrt{3}\)
\(=\left(3\sqrt{3}+6\sqrt{3}-2\sqrt{3}\right):\sqrt{3}\)
=7
4) Ta có: \(\sqrt{50}-3\sqrt{8}+\sqrt{\left(\sqrt{2}+1\right)^2}\)
\(=5\sqrt{2}-6\sqrt{2}+\sqrt{2}+1\)
=1
Đúng 1
Bình luận (0)
Mọi người ơi, giúp mình mấy bài này với ^^

1.
a.
ĐKXĐ: \(x^2-1>0\Rightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)
\(log_2\left(x^2-1\right)=3\)
\(\Rightarrow x^2-1=8\)
\(\Leftrightarrow x^2=9\)
\(\Rightarrow x=\pm3\) (tm)
b.
ĐKXĐ: \(x>0\)
\(log_3x+log_{\sqrt{3}}x+log_{\dfrac{1}{3}}x=6\)
\(\Leftrightarrow log_3x+2log_3x-log_3x=6\)
\(\Leftrightarrow log_3x=3\)
\(\Rightarrow x=3^3=27\)
Đúng 1
Bình luận (0)
c. ĐKXĐ: \(x>0\)
\(log_{\sqrt{2}}^2x+3log_2x+log_{\dfrac{1}{2}}x=2\)
\(\Leftrightarrow\left(2log_2x\right)^2+3log_2x-log_2x=2\)
\(\Leftrightarrow4log_2^2x+2log_2x-2=0\)
\(\Rightarrow\left[{}\begin{matrix}log_2x=-1\\log_2x=\dfrac{1}{2}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=\sqrt{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
d.
ĐKXĐ: \(x>0\)
\(log_{\dfrac{1}{2}}^24x+log_2\dfrac{x^2}{8}=8\)
\(\Leftrightarrow\left(-log_24x\right)^2+log_2x^2-log_28=8\)
\(\Leftrightarrow\left(log_2x+log_24\right)^2+2log_2x-3=8\)
\(\Leftrightarrow\left(log_2x+2\right)^2+2log_2x-11=0\)
\(\Leftrightarrow log_2^2x+6log_2x-7=0\)
\(\Rightarrow\left[{}\begin{matrix}log_2x=1\\log_2x=-7\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{2^7}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giúp mình mấy bài này với mọi người ơi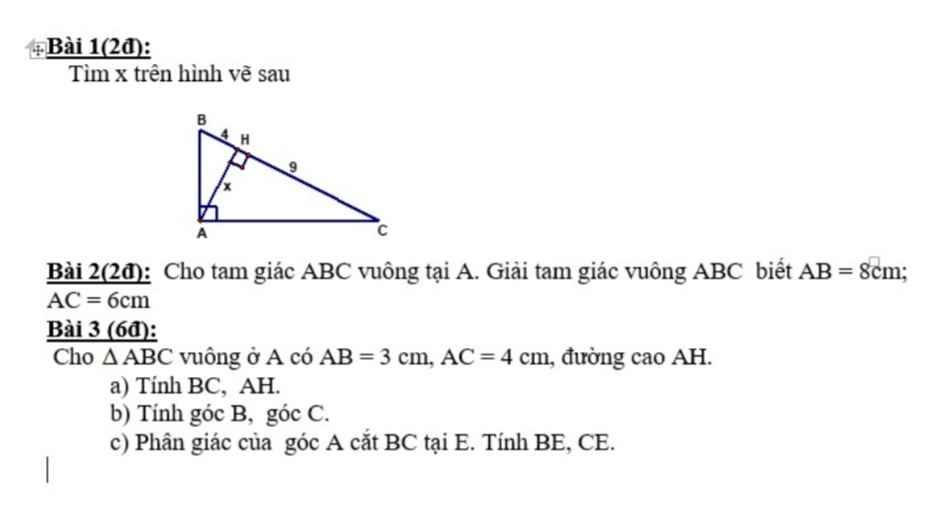
Bài 1:
Áp dụng HTL trong tam giác vuông:
$AH^2=BH.CH$
$\Leftrightarrow x^2=4.9=36$
$\Rightarrow x=6$ (do $x>0$)
Đúng 1
Bình luận (0)
Bài 2:
Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{6^2+8^2}=10$ (cm)
$\sin B=\frac{AC}{BC}=\frac{6}{10}=\frac{3}{5}$
$\Rightarrow \widehat{B}=36,87^0$
$\widehat{C}=90^0-\widehat{B}=90^0-36,87^0=53,13^0$
Đúng 1
Bình luận (0)
Bài 3:
a. Áp dụng định lý Pitago:
$BC=\sqrt{AB^2+AC^2}=\sqrt{3^2+4^2}=5$ (cm)
$AH=\frac{2S_{ABC}}{BC}=\frac{AB.AC}{BC}=\frac{3.4}{5}=2,4$ (cm)
b.
$\sin B=\frac{AC}{BC}=\frac{4}{5}$
$\Rightarrow \widehat{B}=53,13^0$
$\widehat{C}=90^0-\widehat{B}=36,87^0$
c.
Áp dụng tính chất tia phân giác:
$\frac{BE}{CE}=\frac{AB}{AC}=\frac{3}{4}$
$\Rightarrow \frac{BE}{BC}=\frac{3}{7}$
$\Rightarrow BE=BC.\frac{3}{7}=\frac{5.3}{7}=\frac{15}{7}$ (cm)
$CE=BC-BE=5-\frac{15}{7}=\frac{20}{7}$ (cm)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Mọi người ơi giúp mình mấy bài địa này với ạ 

Mọi người ơi giúp mình mấy bài này với (bài khó quá mik làm mãi ko ra mà 8h phải nộp rồi ) giúp mik với huhu

Đề bài : Em hãy tự nghĩ ra các câu đối hay ( Không tra mạng ) trong ngày Tết.
Mọi ngừi ơi, e vã lắm òi.... À nhầm, e vất vả với cái đề bài này nắm òi. Nay e đang cần gấp, mog mọi ngừi giúp e
hoạt động dân gian ngày tết có ông địa cầm quạt phe phẩy ?
tôm khô ăn với củ gì vào ngày tết
món này ngày tết,năm quả trên mâm,nhà nào cũng có,vào khắc giao thừa
Hai câu đầu có đc gọi là câu đối không ?
có mà , mình tìm ở nhà mình
Xem thêm câu trả lời
mọi ngừi ơi giúp mik với mình cần gấp lắm;-; =((

