các cao nhân cho em hỏi làm sao chứng minh BĐT Bunhiacopxki dạng phổ thông đc ạ
TT
Những câu hỏi liên quan
Cho mình hỏi lúc làm bài liên quan đến BĐT Cô si dạng Engel ấy ạ, lúc áp dụng BĐT này thì ở trên có cần phải chứng minh không ạ?
xài bđt phụ mới cần phải chứng minh nhé
mà tau nhớ làm gì có Cô si dạng Engel ??? ._.
Ý mày là không tồn tại cái BĐT tên Cosi dạng engel á:")?
Cauchy-Schwarz dạng Engel thì có :)) còn Cauchy dạng Engel chưa nghe bao giờ ???
Xem thêm câu trả lời
Chứng minh rằng:\(a^2+b^2\ge2ab\)
Mình biết làm rồi chủ yếu cho các bạn kiếm điểm and ad cho em hỏi bao h em ms đc làm CTV ạ
Ta có :
\(a^2+b^2\)\(=a^2-2ab+b^2+2ab\)
\(=\left(a-b\right)^2+2ab\ge2ab\)
Mà CTV là j vậy.
Đúng 0
Bình luận (0)
vào link
https://olm.vn/tin-tuc/Giai-thuong-cong-tac-vien-hoc-ky-2-nam-hoc-2017---2018.html
sẽ hướng dẫn bn cách đăng kí làm cộng tác viên
Đúng 0
Bình luận (0)
Với mọi a,b ta có:
\(\left(a-b\right)^2\ge0\)
<=> \(a^2-2ab+b^2\ge0\)
<=> \(a^2+b^2\ge2ab\)
Dấu "=" xảy ra khi a=b
Đúng 0
Bình luận (0)
mn cho e hỏi cách chứng minh bđt cộng mẫu ạ
Chứng minh \(\dfrac{a^2}{x}+\dfrac{b^2}{y}+\dfrac{c^2}{z}\ge\dfrac{\left(a+b+c\right)^2}{x+y+z}với\left(x;y;z>0\right)\)
Thường thì sẽ sử dụng cái này nhiều nhất
Đầu tiên đi chứng minh
\(\dfrac{a^2}{x}+\dfrac{b^2}{y}\ge\dfrac{\left(a+b\right)^2}{x+y}\\ \Leftrightarrow\dfrac{a^2y+b^2x}{xy}\ge\dfrac{a^2+2ab+b^2}{x+y}\\ \Leftrightarrow a^2xy+\left(bx\right)^2+\left(ay\right)^2+b^2xy\ge a^2xy+2abxy+b^2xy\\ \Leftrightarrow\left(ay\right)^2+\left(bx\right)^2-2abxy\ge0\Leftrightarrow\left(ay-bx\right)^2\ge0\left(đúng\right)\)
Áp dụng 1 lần nữa ta có điều ở trên
Dấu $=$ xảy ra $⇔\dfrac{a}{x}=\dfrac{b}{y}=\dfrac{c}{z}$
Đúng 2
Bình luận (0)

Link (nếu ảnh lỗi): thắc mắc
Mọi người chỉ giúp em làm thế nào để tìm ra cái BĐT phụ này ạ? Và giảng lại giùm em cách chứng minh ạ.Em không c/m đc=(Em cảm ơn.
Trên đây nó ko cho đăng ảnh,mn chịu khó nhập link này vào nha:https://i.imgur.com/xQNntGH.png
Đúng 0
Bình luận (0)
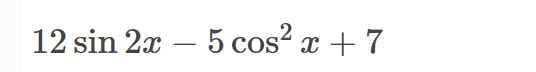
tìm giá trị nhỏ nhất và giá trị lớn nhất(dùng bđt bunhiacopxki)
mọi người giúp em với
\(y=-5\cdot\dfrac{1-cos2x}{2}+12sin2x+7\)
\(=-\dfrac{5}{2}+\dfrac{5}{2}\cdot cos2x+12\cdot sin2x+7\)
\(=12\cdot sin2x+\dfrac{5}{2}\cdot cos2x+\dfrac{9}{2}\)
\(=\dfrac{\sqrt{601}}{2}\cdot\left(\dfrac{12\cdot sin2x}{\dfrac{\sqrt{601}}{2}}+cos2x\cdot\dfrac{5}{2}\cdot\dfrac{2}{\sqrt{601}}\right)+\dfrac{9}{2}\)
\(=\dfrac{\sqrt{601}}{2}\cdot\left(sin2x\cdot cosa+cos2x\cdot sina\right)+\dfrac{9}{2}\)
\(=\dfrac{\sqrt{601}}{2}\cdot sin\left(2x+a\right)+\dfrac{9}{2}\)
\(-1< =sin\left(2x+a\right)< =1\)
=>\(\dfrac{-\sqrt{601}}{2}< =\dfrac{\sqrt{601}}{2}\cdot sin\left(2x+a\right)< =\dfrac{\sqrt{601}}{2}\)
=>\(\dfrac{-\sqrt{601}+9}{2}< =y< =\dfrac{\sqrt{601}+9}{2}\)
\(y_{min}\) khi sin(2x+a)=-1
=>\(2x+a=-\dfrac{pi}{2}+k2pi\)
=>\(2x=-\dfrac{pi}{2}-a+k2pi\)
=>\(x=-\dfrac{pi}{4}-\dfrac{a}{2}+kpi\)
\(y_{max}\) khi sin(2x+a)=1
=>\(2x+a=\dfrac{pi}{2}+k2pi\)
=>\(x=\dfrac{pi}{4}-\dfrac{a}{2}+kpi\)
Đúng 0
Bình luận (0)
Chứng minh định lí bunhiacopxki dưới dạng phân thức
Lời giải:
Cho $a_1,a_2,...,a_n>0; b_1,b_2,...,b_n>0$. Khi đó:
\(\frac{a_1^2}{b_1}+\frac{a_2^2}{b_2}+...+\frac{a_n^2}{b_n}\geq \frac{(a_1+a_2+....+a_n)^2}{b_1+b_2+...+b_n}\)
Đúng 1
Bình luận (0)
cho ∆ABC nhọn, vẽ 3 đường cao BD,CE,AK cắt nhau tại I
a/ chứng minh ∆ADB đồng dạng ∆AEC
b/ chứng minh ∆EIB đồng dạng ∆DIC
c/ gọi J là giao điểm của DE và BC, lấy điểm M thuộc AK sao cho EM song song AC và cắt Ạ tại N, chứng minh EN bằng EM
a: Xet ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạngvới ΔAEC
b: Xet ΔIEB vuông tại E và ΔIDC vuông tại D có
góc EIB=góc DIC
=>ΔIEB đồng dạng với ΔIDC
Đúng 0
Bình luận (0)
-Các dạng chứng minh đẳng thức sin, cos, tan, cot thường gặp, phổ biến( hay các dạng mà các bạn đã từng làm, ghi lại và chỉ mình cách làm).
-Cách chứng minh.
Cảm ơn trước!!!
cho tam giác ABC kẻ các đường cao AD BC cắt nhau tại H
a) chứng minh tam giác ADC đồng dạng với tam giác BKC
b) trên tia đối của tia DA xác định điểm M sao cho DH = DM chứng minh tam giác MBH cân
c) chứng minh CAM = CBM
mong mn giúp với ạ em cần ngay tối nay ạ
em cảm ơn mn trước ạ
a) Xét tam giác ADC và tam giác BKC có:
\(\hept{\begin{cases}\widehat{C}\text{ chung}\\\widehat{BKC}=\widehat{ADC}\left(=90^{\text{o}}\right)\end{cases}}\Rightarrow\Delta ADC\approx\Delta BKC\)(g-g)
b) Xét tam giác BDM và tam giác BDH có :
\(\hept{\begin{cases}BD\text{ chung}\\\widehat{BDM}=\widehat{BDH}\left(=90^{\text{o}}\right)\\MD=DH\end{cases}}\Rightarrow\Delta BDM=\Delta BDH\left(c.g.c\right)\)
=> \(\widehat{BMD}=\widehat{BHD}\left(\text{góc tương ứng}\right)\)
=> \(\Delta MBH\text{ cân tại B}\)
c) Xét tam giác AHK và tam giác BMD có :
\(\hept{\begin{cases}\widehat{BMD}=\widehat{AHK}\left(=\widehat{BHD}\right)\\\widehat{BDM}=\widehat{HKA}\left(=90^{\text{o}}\right)\end{cases}\Rightarrow\Delta AKH\approx\Delta BMD\left(g-g\right)}\)
=> \(\Rightarrow\widehat{DBM}=\widehat{KAH}\text{ hay }\widehat{CBM}=\widehat{CAM}\)





