Tìm x để biểu thức có giá trị Max: B=2+2*x+x^2
TL
Những câu hỏi liên quan
Tìm x để biểu thức có giá trị Max
B=2+2*x+x^2
Tìm x để biểu thức có giá trị Max B=2+2*x+x2
Cho biểu thức A=√x +5/2√x -4 ; B= √x/√x -2
Tìm giá trị của x để biểu thức B/A có giá trị nguyên.
Xem chi tiết
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne4\end{matrix}\right.\)
Ta có: \(\dfrac{B}{A}=\dfrac{\sqrt{x}}{\sqrt{x}-2}:\dfrac{\sqrt{x}+5}{2\sqrt{x}-4}\)
\(\Leftrightarrow\dfrac{B}{A}=\dfrac{\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{2\left(\sqrt{x}-2\right)}{\sqrt{x}+5}\)
\(\Leftrightarrow\dfrac{B}{A}=\dfrac{2\sqrt{x}}{\sqrt{x}+5}\)
Để \(\dfrac{B}{A}\) nguyên thì \(2\sqrt{x}⋮\sqrt{x}+5\)
\(\Leftrightarrow2\sqrt{x}+10-10⋮\sqrt{x}+5\)
mà \(2\sqrt{x}+10⋮\sqrt{x}+5\)
nên \(-10⋮\sqrt{x}+5\)
\(\Leftrightarrow\sqrt{x}+5\inƯ\left(-10\right)\)
\(\Leftrightarrow\sqrt{x}+5\in\left\{1;-1;2;-2;5;-5;10;-10\right\}\)
\(\Leftrightarrow\sqrt{x}+5\in\left\{5;10\right\}\)(Vì \(\sqrt{x}+5\ge5\forall x\) thỏa mãn ĐKXĐ)
\(\Leftrightarrow\sqrt{x}\in\left\{0;5\right\}\)
hay \(x\in\left\{0;25\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{0;25\right\}\)
Vậy: Để \(\dfrac{B}{A}\) nguyên thì \(x\in\left\{0;25\right\}\)
Đúng 4
Bình luận (0)
cho biểu thức C= x/2x-2 + x^2+1/2-2x^2
a) Tìm x để biểu thức C có nghĩa
b) Rút gọn biểu thức C*c.
c)Tìm giá trị của x để biểu thức có giá trị -0,5
Cho biểu thức \(C=\dfrac{x}{2x-2}-\dfrac{x^2+1}{2-2x^2}\).
a. Tìm x để biểu thức C có nghĩa.
b.Rút gọn biểu thức C.
c.Tìm giá trị của x để giá trị của biểu thức C = \(\dfrac{-1}{2}\).
d. Tìm x để giá trị của phân thức C > 0.
\(a,ĐK:x\ne1;x\ne-1\\ b,C=\dfrac{x^2+x+x^2+1}{2\left(x-1\right)\left(x+1\right)}=\dfrac{2x^2+2x+1}{2x^2-2}\\ c,C=-\dfrac{1}{2}\Leftrightarrow2-2x^2=2x^2+2x+1\\ \Leftrightarrow4x^2+2x-1=0\\ \Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\sqrt{5}-1}{4}\\x=\dfrac{-\sqrt{5}-1}{4}\end{matrix}\right.\\ d,C>0\Leftrightarrow2x^2-2>0\left(2x^2+2x+1>0\right)\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)>0\\ \Leftrightarrow\left[{}\begin{matrix}x>1\\x< -1\end{matrix}\right.\)
Đúng 0
Bình luận (1)
1) cho Ax/x-1 + x/x+1 (x ko bằng +-1) và BX^2-x/x^2-1 (x ko bằng +-1)a)rút gọn A và tính A khi x2b)Rút gọn B và tìm x để B2/5c)tìm x thuộc Z để (A,B)thuộc Z 2)A (2+x/2-x - 4x^2/x^2-4 - 2-x/2+x) : x^2 - 3x/2x^2 - x^3a)rút gọn biểu thức A b) tính giá trị biểu thức A khi /x-5/2c)tìm x để A03)B x+2/x+3 - 5/x^2+x-6 - 1/2-xa)rút gọn biểu thức B b)tìm x để B3/2 c) tìm giá trị nguyên của x để B có giả trị nguyên4)C (2x/2x^2-5x+3 - 5/2x-3) : (3+2/1-x)a)rút gọn biểu thức C b) tìm giá trị nguyên...
Đọc tiếp
1) cho A=x/x-1 + x/x+1 (x ko bằng +-1) và B=X^2-x/x^2-1 (x ko bằng +-1)
a)rút gọn A và tính A khi x=2
b)Rút gọn B và tìm x để B=2/5
c)tìm x thuộc Z để (A,B)thuộc Z
2)A =(2+x/2-x - 4x^2/x^2-4 - 2-x/2+x) : x^2 - 3x/2x^2 - x^3
a)rút gọn biểu thức A b) tính giá trị biểu thức A khi /x-5/=2
c)tìm x để A>0
3)B= x+2/x+3 - 5/x^2+x-6 - 1/2-x
a)rút gọn biểu thức B b)tìm x để B=3/2 c) tìm giá trị nguyên của x để B có giả trị nguyên
4)C= (2x/2x^2-5x+3 - 5/2x-3) : (3+2/1-x)
a)rút gọn biểu thức C b) tìm giá trị nguyên của biểu thức C biết :/2x-1/=3
c)tìm x để B >1 d) tìm giá trị nhỏ nhất của biểu thức C
5)D=(1 + x/x^2+1) : (1/x-1 - 2x/x^3+x-x^2-1)
a)rút gọn biểu thức D
b)tìm giá trị của x sao cho D<1
c)tìm giá trị nguyên của x để B có giá trị nguyên
bạn viết thế này khó nhìn quá
nhìn hơi đau mắt nhá bạn hoa mắt quá
Cho biểu thức \(P=\frac{2x^2+bx+c}{x^2+1}\)
Tìm các giá trị của b và c để biểu thức P có min=1 và max=3
( a = 3; b =-4; c = 1)
TXĐ : D = R.
Tọa độ đỉnh I (2/3; -1/3).
Trục đối xứng : x = 2/3
Tính biến thiên :
a = 3 > 0 hàm số nghịch biến trên (-∞; 2/3). và đồng biến trên khoảng 2/3 ; +∞)
bảng biến thiên :
x | -∞ | 2/3 | +∞ | ||
y | +∞ | -1/3 | +∞ |
Các điểm đặc biệt :
(P) giao trục hoành y = 0 : 3x2 – 4x + 1 = 0 <=> x = 1 v x = ½
(P) giao trục tung : x = 0 => y = 1
Đồ thị :
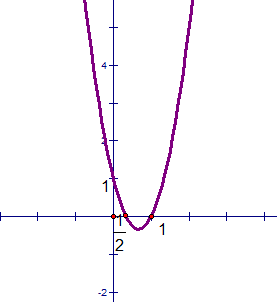
P/s: Bn tham khảo nhé, mk ko chắc đâu
Đúng 0
Bình luận (0)
cho biểu thuiwcs C= x/2x-2 + x^2+1/2-2x^2
a) tìm x để biểu thức C có nghĩa
b) rút gọn biểu thức ÙC
c) tìm giá trị của x để giá trị biểu thức C= -1/2
tìm m để pt: \(x^2-2mx+2m^2-4m+3=0\)
có 2 nghiệm x1,x2 và biểu thức A=\(x1^2+x2^2+3x1x2\)
đạt giá trị Max
\(\Delta'=m^2-\left(2m^2-4m+3\right)=-m^2+4m-3\)
\(=-\left(m^2-4m+4-4\right)-3=-\left(m-2\right)^2+1\)
Để pt trên có 2 nghiệm x1 ; x2 khi \(0\le-\left(m-2\right)^2+1\le1\)
Theo Vi et : \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m^2-4m+3\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2+x_1x_2\)
\(=4m^2+2m^2-4m+3=6m^2-4m+4\)
bạn kiểm tra lại đề xem có vấn đề gì ko ?
Đúng 1
Bình luận (0)
\(\Delta'=m^2-\left(2m^2-4m+3\right)=-m^2+4m-3\ge0\Rightarrow1\le m\le3\)
Theo Viet: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=2m^2-4m+3\end{matrix}\right.\)
\(A=\left(x_1+x_2\right)^2+x_1x_2\)
\(=\left(2m\right)^2+2m^2-4m+3\)
\(=6m^2-4m+3\)
Xét hàm \(f\left(m\right)=6m^2-4m+3\) trên \(\left[1;3\right]\)
\(-\dfrac{b}{2a}=\dfrac{1}{3}< 1;a=6>0\Rightarrow f\left(m\right)\) đồng biến trên \(\left[1;3\right]\)
\(\Rightarrow f\left(m\right)_{max}=f\left(3\right)=45\) khi \(m=3\)
Đúng 3
Bình luận (0)



