Tìm tất cả các cặp số nguyên x,y thỏa mãn x(x2+x+1)=4y-1
H24
Những câu hỏi liên quan
H24
1 tháng 6 2023 lúc 13:24
tìm tất cả các cặp số nguyên (x, y) thỏa mãn: x(x2 - y) + (y - 3)(x2 + 1) = 0
tìm tất cả các cặp số nguyên x, y thỏa mãn x2+x = 32019y+1
- Với \(y=0\Rightarrow x^2+x=3^0+1=2\)
\(\Rightarrow x^2+x-2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
- Với \(y< 0\Rightarrow3^{2019y}\) không phải số nguyên \(\Rightarrow3^{2019y}+1\) không phải số nguyên (loại)
- Với \(y>0\Rightarrow3^{2019y}⋮3\Rightarrow3^{2019y}+1\) chia 3 dư 1
Mà \(x^2+x=x\left(x+1\right)\) là tích 2 số nguyên liên tiếp nên chia 3 chỉ có thể dư 0 hoặc 2
\(\Rightarrow x^2+x\ne3^{2019y}+1\) với mọi \(y>0\) \(\Rightarrow\) phương trình ko có nghiệm nguyên
Vậy pt đã cho có đúng 2 cặp nghiệm nguyên là \(\left(x;y\right)=\left(-2;0\right);\left(1;0\right)\)
Đúng 2
Bình luận (1)
@ Ha Dung vì khi y < 0 thì y = -k (k 
N)
⇒ 32019y = 3-2019k = ( N)
()2019k không phải là số nguyên vậy 32019y không phải là số nguyên em nhé.
Đúng 0
Bình luận (0)
Biết rằng trong tất cả các cặp (x; y) thỏa mãn:
log
2
x
2
+
y
2
+
2
≤
log
2
x
+
y
-
1...
Đọc tiếp
Biết rằng trong tất cả các cặp (x; y) thỏa mãn: log 2 x 2 + y 2 + 2 ≤ log 2 x + y - 1 . Chỉ có duy nhất một cặp (x; y) thỏa mãn: 3x + 4y - m = 0 . Khi đó hãy tính tổng tất cả các giá trị m tìm được?
A. 20
B. 46
C. 28
D. 14
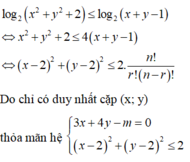
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
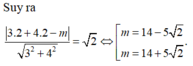
Chọn C.
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số nguyên (x,y) thỏa mãn \(x\left(1+x+x^2\right)=4y\left(y-1\right)\)
Mình gợi ý phần đầu nè. Xét \(x=0\) riêng được \(y=0\) hoặc \(y=1\).
Xét \(x\ne0\). Khi đó \(x\) và \(x^2+x+1\) nguyên tố cùng nhau với mọi \(x\) nguyên khác 0.
(Ở đây ta chỉ định nghĩa 2 số nguyên tố cùng nhau là 2 số có ước chung lớn nhất là 1 nên số âm vẫn được).
Để CM điều này ta gọi \(d=gcd\left(x^2+x+1,x\right)\) thì \(1⋮d\).
Vế trái là một số chia hết cho 4 nên trong 2 số \(x\) và \(x^2+x+1\) phải có một số chia hết cho 4
(Nếu mỗi số đều chia hết cho 2 thì không thể nguyên tố cùng nhau)
Trường hợp 1: \(x⋮4\) còn \(x^2+x+1\) lẻ.
Do \(y\) và \(y-1\) có 1 số chẵn và 1 số lẻ nên số chẵn sẽ là ước của \(x\) còn số lẻ là ước của \(x^2+x+1\).
Tức là có 2 trường hợp: \(x=4y\) và \(x=4\left(y-1\right)\).
Trường hợp 2 ngược lại.
Tới đây bạn tự giải được nha.
Đúng 0
Bình luận (0)
\(x\left[1+x+x^2\right]=4y\left[y-1\right]\)
\(\Leftrightarrow x^3+x^2-4y^2+x+4y=0\)
\(\Leftrightarrow x^2\left[x+1\right]+x-4y^2+4y=0\)
\(\Leftrightarrow\Delta=b^2-4ac=1-16xy+16xy^2-16y+16y^2\)
\(\Rightarrow\orbr{\begin{cases}x1=\frac{-1+\sqrt{1-16xy+16xy^2-16y+16y^2}}{2x+2}\\x2=\frac{-1-\sqrt{1-16xy+16xy^2-16y+16y^2}}{2x+2}\end{cases}}\)
đến đây tự làm tiếp nhé
Đúng 0
Bình luận (0)
Có: |
Vì |
Giả sử |
Vì |
Do |
Khi Vậy có hai cặp số nguyên |
(1)
, nên từ 
và 
chẵn.
lẻ và 
là số chính phương, 
nên 
và
cũng là hai số chính phương.
, có 
.
thỏa mãn yêu cầu bài toán là: 
Đúng 0
Bình luận (0)
Tìm tất cả các cặp số nguyên x, y thỏa mãn: y.(x2 + 2) = x + 2
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
. Tìm m để tồn tại duy nhất cặp (x;y) sao cho
x...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 . Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 10 - 2 2
B. 10 - 2 h o ặ c 10 + 2
C. 10 - 2 2 h o ặ c 10 + 2 2
D. 10 - 2
Chọn C.
Phương pháp: Đưa bài toán về tìm m để hệ có nghiệm duy nhất.
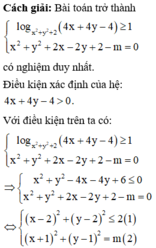
Đúng 0
Bình luận (0)
Trong tất cả các cặp (x;y) thỏa mãn
log
x
2
+
y
2
+
2
2
x
-
4
y
+
6
≥
1
, tìm m để tồn tại duy nhất cặp (x;y) sao cho
x...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn log x 2 + y 2 + 2 2 x - 4 y + 6 ≥ 1 , tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
A. 13 - 3 v à 13 + 3
B. 13 - 3
C. 13 - 3 2
D. 13 - 3 2 và 13 + 3 2
Trong tất cả các cặp (x;y) thỏa mãn
l
o
g
x
2
+
y
2
+
2
4
x
+
4
y
-
4
≥
1
Tìm m để tồn tại duy nhất cặp (x;y) sao cho...
Đọc tiếp
Trong tất cả các cặp (x;y) thỏa mãn l o g x 2 + y 2 + 2 4 x + 4 y - 4 ≥ 1 Tìm m để tồn tại duy nhất cặp (x;y) sao cho x 2 + y 2 + 2 x - 2 y + 2 - m = 0 .
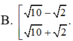
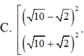
Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số (x;y) thỏa mãn
log
x
2
+
y
2
+
2
4
x
+
4
y
-
6
+
m...
Đọc tiếp
Tìm tập S tất cả các giá trị thực của tham số m để tồn tại duy nhất cặp số (x;y) thỏa mãn log x 2 + y 2 + 2 4 x + 4 y - 6 + m 2 ≥ 1 và x 2 + y 2 + 2 x - 4 y + 1 = 0 .
A. S = - 5 ; 5
B. S = - 7 ; - 5 ; - 1 ; 5 ; 7
C. S = - 5 ; - 1 ; 1 ; 5
D. S = - 1 ; 1
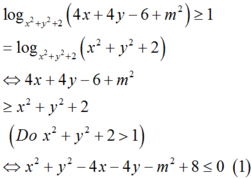
Ta có
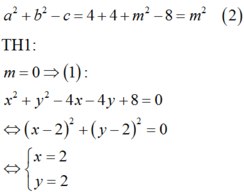
Cặp số x ; y = 2 ; 2 không thỏa mãn điều kiện .
Tập hợp các cặp số (x;y) thỏa mãn (1) là hình tròn C1(kể cả biên) tâm I1(2;2) bán kính R 1 = m .
Tập hợp các cặp số (x;y) thỏa mãn (2) là đường tròn C2 tâm I 2 - 1 ; 2 bán kính R 2 = 1 + 4 - 1 = 2 .
Để tồn tại duy nhất cặp số (x;y) thỏa mãn 2 điều kiện (1) và (2) Xảy ra 2 trường hợp sau:
TH1: C1; C2tiếp xúc ngoài
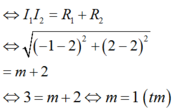
TH2: C1; C2 tiếp xúc trong và
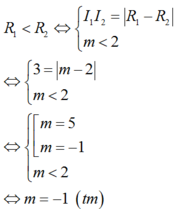
Vậy S = - 1 ; 1 .
Chọn D.
Đúng 0
Bình luận (0)
Tìm tất cả các số nguyên x,y . thỏa mãn phương trình : x2+6xy+5y2-4y-8=0
\(x^2+6xy+5y^2-4y-8=0\)
\(\Leftrightarrow (x^2+6xy+9y^2)-(4y^2+4y+1)=7\)
\(\Leftrightarrow (x+3y)^2-(2y+1)^2=7\)
\(\Leftrightarrow (x+y-1)(x+5y+1)=7\)
Vì x,y nguyên nên ta có các trường hợp sau:
TH1: \(\begin{cases} x+y-1=1\\ x+5y+1=7 \end{cases} \Leftrightarrow \begin{cases} x+y-1=1\\ 4y+2=6 \end{cases} \Leftrightarrow \begin{cases} x=1\\ y=1 \end{cases}\)
Các TH còn lại bạn tự làm nhé
Đúng 1
Bình luận (0)
\(x^2+6xy+5y^2-4y-8=0\)
\(\Leftrightarrow\left(x^2+6xy+9y^2\right)-4y^2-4y-1-7=0\)
\(\Leftrightarrow\left(x+3y\right)^2-\left(2y+1\right)^2=7\)
\(\Leftrightarrow\left(x+5y+1\right)\left(x+y-1\right)=7=\left[{}\begin{matrix}1.7\\7.1\\\left(-1\right).\left(-7\right)\\\left(-7\right).\left(-1\right)\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x+5y+1=1;x+y-1=7\\x+5y+1=7;x+y-1=1\\x+5y+1=-1;x+y-1=-7\\x+5y+1=-7;x+y-1=-1\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=10;y=-2\left(nhận\right)\\x=y=1\left(nhận\right)\\x=y=1\left(nhận\right)\\x=10;y=-2\left(nhận\right)\end{matrix}\right.\)
-Vậy các cặp số (x,y) là \(\left(10;-2\right);\left(1;1\right)\)
Đúng 1
Bình luận (0)