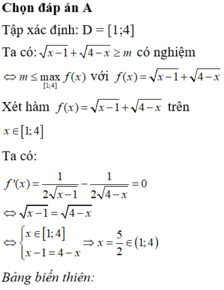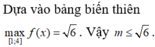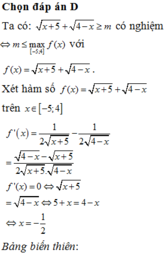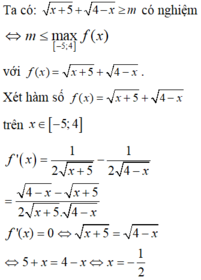Tìm tất cả giá trị nguyên của x, sao cho: (x + 7) . (4 - x) > 0
LT
Những câu hỏi liên quan
cho biểu thức P=4√x +3/x+√x + √x/√x + 1, với x lớn hơn 0. Tìm tất cả các giá trị nguyên của x để P nhận giá trị nguyên
Xem chi tiết
Ta có: \(P=\dfrac{4\sqrt{x}+3}{x+\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\dfrac{4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}+\dfrac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x+4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\dfrac{\sqrt{x}+3}{\sqrt{x}}\)
Để P nguyên thì \(\sqrt{x}+3⋮\sqrt{x}\)
mà \(\sqrt{x}⋮\sqrt{x}\)
nên \(3⋮\sqrt{x}\)
\(\Leftrightarrow\sqrt{x}\inƯ\left(3\right)\)
\(\Leftrightarrow\sqrt{x}\in\left\{1;-1;3;-3\right\}\)
mà \(\sqrt{x}>0\forall x\) thỏa mãn ĐKXĐ
nên \(\sqrt{x}\in\left\{1;3\right\}\)
\(\Leftrightarrow x\in\left\{1;9\right\}\)
Kết hợp ĐKXĐ, ta được: \(x\in\left\{1;9\right\}\)
Vậy: Để P nguyên thì \(x\in\left\{1;9\right\}\)
Đúng 1
Bình luận (0)
Cho biểu thức P=\(\frac{4\sqrt{x}+3}{x+\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1},\) với x>0.Tìm tất cả các giá trị nguyên của x để P nhận giá trị nguyên
\(P=\frac{4\sqrt{x}+3}{x+\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\)
\(P=\frac{4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}+\frac{\sqrt{x}}{\sqrt{x}+1}=\frac{4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}+\frac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{x+4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}\inℤ\Leftrightarrow x+4\sqrt{x}+3⋮\sqrt{x}\)
Giải tiếp nhé sau đó thử chọn :V
Đúng 0
Bình luận (0)
\(p=\frac{4\sqrt{x}+3}{x+\sqrt{x}}+\frac{\sqrt{x}}{\sqrt{x}+1}\)
\(=\frac{4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}+\frac{x}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{x+\sqrt{x}+3\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}=\frac{\left(\sqrt{x}+3\right)\left(\sqrt{x}+1\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}\)
\(=\frac{\sqrt{x}+3}{\sqrt{x}}=1+\frac{3}{\sqrt{x}}\)
Để \(x\in Z\Rightarrow P\in Z\)
\(\Rightarrow\sqrt{x}\inƯ\left(3\right)= \left\{-3;3\right\}\)
\(\Leftrightarrow x=9\left(t.mĐKXĐ\right)\)
Đúng 0
Bình luận (0)
Với x >0
\(P=\frac{x+4\sqrt{x}+3}{\sqrt{x}\left(\sqrt{x}+1\right)}=\frac{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}{\sqrt{x}\left(\sqrt{x}+1\right)}=\frac{\sqrt{x}+3}{\sqrt{x}}=1+\frac{3}{\sqrt{x}}\)
Để P nhận giá trị nguyên thì \(\frac{3}{\sqrt{x}}\in Z\Leftrightarrow\sqrt{x}\in U\left(3\right)\Leftrightarrow\sqrt{x}\in\left\{1,3\right\}\)<=> x thuộc {1, 9}
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho biểu thức Aleft(frac{2}{sqrt{x-2}}+frac{3}{2sqrt{x}+1}-frac{5sqrt{x}-7}{2x-3sqrt{x}-2}right):frac{2sqrt{x}+3}{5x-10sqrt{x}}xne4;x01. Rút gọn biểu thức A2. Tìm tất cả các giá trị của x sao cho Afrac{3sqrt{x}+2}{sqrt{x}+2}3. Tìm giá trị cũa sao cho Agefrac{15}{7}4. Tìm x sao cho A nhận giá trị là một số nguyên
Đọc tiếp
Cho biểu thức
\(A=\left(\frac{2}{\sqrt{x-2}}+\frac{3}{2\sqrt{x}+1}-\frac{5\sqrt{x}-7}{2x-3\sqrt{x}-2}\right):\frac{2\sqrt{x}+3}{5x-10\sqrt{x}}\)\(x\ne4;x>0\)
1. Rút gọn biểu thức A
2. Tìm tất cả các giá trị của x sao cho \(A=\frac{3\sqrt{x}+2}{\sqrt{x}+2}\)
3. Tìm giá trị cũa sao cho \(A\ge\frac{15}{7}\)
4. Tìm x sao cho A nhận giá trị là một số nguyên
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm
x
-
1
+
4
-
x
≥
m
. A.
m
≤
6
B.
m
≥
6
C.
m
≤
3
D.
3
≤
m
≤
6
Đọc tiếp
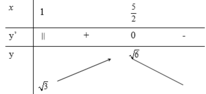
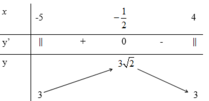
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm x - 1 + 4 - x ≥ m .
A. m ≤ 6
B. m ≥ 6
C. m ≤ 3
D. 3 ≤ m ≤ 6
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm:
x
+
5
+
4
-
x
≥
m
A. 1 B. 2 C. 3 D. 4
Đọc tiếp
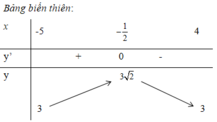
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 - x ≥ m
A. 1
B. 2
C. 3
D. 4
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm:
x
+
5
+
4
-
x
≥
m
A. 1 B. 2 C. 3 D. 4
Đọc tiếp
Tìm tất cả các giá trị nguyên dương của tham số m sao cho bất phương trình sau có nghiệm: x + 5 + 4 - x ≥ m
A. 1
B. 2
C. 3
D. 4
tìm x thuộc số nguyên sao cho biều thức A = 7-x tất cả trên x-5 đạt giá trị lớn nhất
x = (5*a+7)
_____
(a+1)
a) Tìm tất cả các tham số m nguyên để \(F\left(x\right)=\dfrac{7}{x^2+\dfrac{1}{2}m}\) có nghiệm x nguyên và F(x) là số nguyên dương.
b) Với mọi \(m\ge0\), tìm giá trị lớn nhất của F(x).
Với mọi m < 0, tìm giá trị nhỏ nhất của F(x).
Tìm tất cả giá trị của x sao cho x^2 - 2xy + y^2 + 3x - 3y - 4 = 0 biết y = 3
\(x^2-2xy+y^2+3x-3y-4=0\)
\(\Leftrightarrow\left(x-y\right)^2+3\left(x-y\right)-4=0\)
\(\Leftrightarrow\left(x-y\right)\left(x-y+3\right)-4=0\)
Thay y = 3 vào biểu thức trên ta được :
\(x\left(x-3\right)-4=0\)
\(\Leftrightarrow x^2-3x-4=0\Leftrightarrow\left(x-4\right)\left(x+1\right)=0\Leftrightarrow x=4;x=-1\)
Vậy với y = 3 thì x = 4 ; x = -1
Thay y = 3 vào bthuc ta được :
x2 - 6x + 9 + 3x - 9 - 4 = 0
<=> x2 - 3x - 4 = 0
<=> ( x + 1 )( x - 4 ) = 0
<=> x = -1 hoặc x = 4