các thầy cô giúp em với ạ
NP
Những câu hỏi liên quan
các thầy cô giúp em với ạ

Thầy cô các anh chị và các bạn giúp em với ạ, em cần gấp ạ

Câu 1 Đề sai bạn
VD a = 5 ; b = 4
=> a2 - ab + b = 52 - 5.4 + 4 = 9 \(⋮\)9
nhưng a ; b \(⋮̸\)3
Đúng 0
Bình luận (0)
Dạ Em chào Thầy/Cô ạ!
Dạ Thầy/Cô giúp em giải bài này với ạ !
Em xin cảm ơn ạ

1: vecto AC=(-1;-7)
=>VTPT là (-7;1)
PTTS là:
x=3-t và y=6-7t
Phương trình AC là:
-7(x-3)+1(y-6)=0
=>-7x+21+y-6=0
=>-7x+y+15=0
2: Tọa độ M là:
x=(3+2)/2=2,5 và y=(6-1)/2=2,5
PTTQ đường trung trực của AC là:
-7(x-2,5)+1(y-2,5)=0
=>-7x+17,5+y-2,5=0
=>-7x+y+15=0
3: \(AB=\sqrt{\left(-1-3\right)^2+\left(3-6\right)^2}=5\)
Phương trình (A) là:
(x-3)^2+(y-6)^2=AB^2=25
Đúng 1
Bình luận (1)
Dạ em chào Thầy/Cô,
Thầy/Cô giải giúp em Câu 3 với ạ
Em cảm ơn nhiều ạ

1, VTCP \(\overrightarrow{AC}=\left(-2;2\right)\); A(4;3)
PTTS : \(\left\{{}\begin{matrix}x=4+2t\\y=3-2t\end{matrix}\right.\)( t là tham số )
VTPT ( -2;-2) ; A(4;3)
PTTQ : \(-2\left(x-4\right)-2\left(y-3\right)=0\Leftrightarrow-2x-2y+14=0\Leftrightarrow x+y-7=0\)
2, AB : \(VTCP\overrightarrow{AB}=\left(-10;-2\right)\)
Do delta vuông góc với AB nên VTCP AB là VTPT đt delta
delta \(-10\left(x-2\right)-2\left(y-5\right)=0\Leftrightarrow-10x-2y+30=0\Leftrightarrow5x+y-15=0\)
3, pt đường tròn có dạng \(\left(x+6\right)^2+\left(y-1\right)^2=R^2\)
do pt (C1) thuộc A nên \(\left(4+6\right)^2+\left(3-1\right)^2=R^2\Leftrightarrow104=R^2\)
=> \(\left(C1\right):\left(x+6\right)^2+\left(y-1\right)^2=104\)
4, tâm \(I\left(3;4\right)\)
\(R=\dfrac{AC}{2}=\dfrac{\sqrt{4+4}}{2}=\dfrac{\sqrt{8}}{2}\Rightarrow R^2=2\)
\(\left(C2\right):\left(x-3\right)^2+\left(y-4\right)^2=2\)
Đúng 1
Bình luận (0)
Nhờ thầy cô và các bạn giúp đỡ em với ạ
Đọc tiếp
Nhờ thầy cô và các bạn giúp đỡ em với ạ
Nhờ thầy cô và các bạn giúp đỡ với ạ. Em cám ơn nhiều ạ!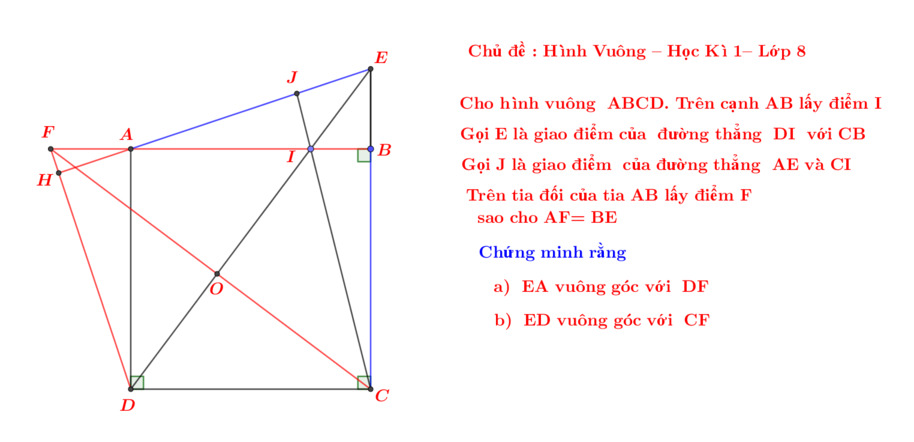
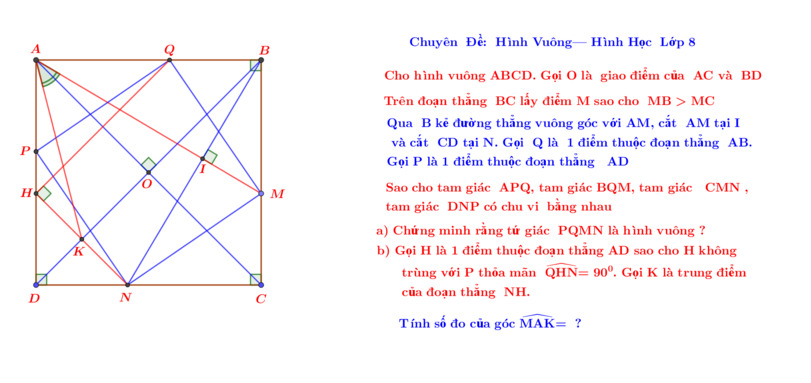
Em xin phép nhờ quý thầy cô và các bạn giúp đỡ với ạ, em cám ơn nhiều ạ
-Để mình suy nghĩ ngồi làm cho bạn nhé.
Đúng 0
Bình luận (0)
-Vì bài dài quá nên mình nói tóm tắt:
a) -Bạn chứng minh △ABM = △BCN (g-c-g) do có \(AB=BC\) , \(\widehat{BCN}=\widehat{ABM}=90^0\),\(\widehat{NBC}=\widehat{MAB}\) (bạn tự chứng minh).
-Suy ra: \(BM=CN\) .
-Suy ra 2 điều:
+\(QM^2-BQ^2=MN^2-MC^2\)
+\(QM+BQ=MN+MC\) (1)
\(QM^2-BQ^2=MN^2-MC^2\)
\(\Rightarrow\left(QM-BQ\right)\left(QM+BQ\right)=\left(MN-MC\right)\left(MN+MC\right)\)
\(\Rightarrow QM-BQ=MN-MC\) (2)
-Từ (1),(2) suy ra \(QM=MN\) nên △BMQ=△CNM (ch-cgv).
\(\Rightarrow\) MQ vuông góc với MN (bạn tự c/m).
\(QM=MN\) nên \(BQ=MC\) nên \(AQ=BM\Rightarrow PQ^2-AP^2=QM^2-BQ^2;QM+BQ=PQ+AP\)
Nên \(PQ=QM;\Delta APQ=\Delta BQM\) nên PQ⊥QM ; AP=BQ nên PQ=AQ
-Từ PQ=AQ bạn tự c/m PN=PQ (theo sườn mình đã cho) rồi sau đó c/m tam giác APQ=tam giác DNP rồi từ đó suy ra PQ vuông góc PN
.......
Đúng 0
Bình luận (1)
Nhờ thầy cô và các bạn trong nhóm giúp đỡ em với ạ!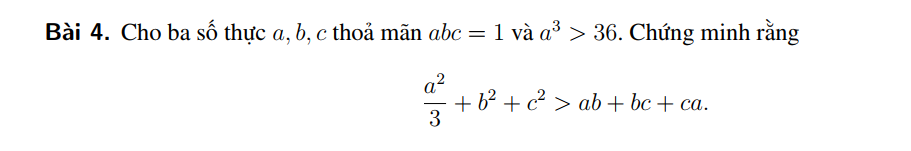
Từ GT \(\Leftrightarrow a>0;bc>0\)
\(BĐT\Leftrightarrow\dfrac{a^2}{3}+\left(b+c\right)^2-3bc-a\left(b+c\right)\ge0\\ \Leftrightarrow\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\ge0\)
Vì \(a^3>36\) nên
\(\dfrac{1}{3}+\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}-\dfrac{3}{a^2}\\ >\left(\dfrac{b+c}{a}\right)^2-\dfrac{b+c}{a}+\dfrac{1}{4}=\left(\dfrac{b+c}{a}-\dfrac{1}{2}\right)^2\ge0\)
Đúng 2
Bình luận (1)
x/15 = -1/3
các bạn và thầy cô giúp em với ạ !
Ta có : \(\dfrac{x}{15}\text{=}\dfrac{-1}{3}\)
\(\Rightarrow\dfrac{x}{15}\text{=}\dfrac{-5}{15}\)
\(\Rightarrow x\text{=}-5\)
Đúng 3
Bình luận (0)
\(\dfrac{x}{15}\)=\(\dfrac{-1}{3}\)
⇒x.3=15. -1
⇒x.3=-15
⇒x =-15 ; 3
⇒x =-5
Vậy x=-5
Đúng 1
Bình luận (0)






