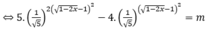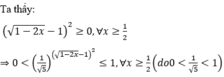Khi m € [ a;b] thì phương trình (2m-1)Sinx + Cosx = m+5 có nghiệm. Tính a+b!!
H24
Những câu hỏi liên quan
Cho A (-2;3) và B [m-1;m+1]. Ta có A ∩ B ∅ khi và chỉ khi m thuộc: A.
(
-
∞
;
-
3
)
∪
[
4
;
+
∞
)
. B. [-3; 4). C. [-1; 2). D. (-∞; -3].
Đọc tiếp
Cho A = (-2;3) và B = [m-1;m+1]. Ta có A ∩ B = ∅ khi và chỉ khi m thuộc:
A. ( - ∞ ; - 3 ) ∪ [ 4 ; + ∞ ) .
B. [-3; 4).
C. [-1; 2).
D. (-∞; -3].
Đáp án: A
A ∩ B = ∅ ⇔ m + 1 ≤ - 2 h o ặ c m - 1 ≥ 3 ⇔ m ≤ - 3 h o ặ c m ≥ 4 ⇒ m ∈ ( - ∞ ; - 3 ] ∪ [ 4 ; + ∞ ) .
Đúng 0
Bình luận (0)
Cho hệ phương trình có tham số m:
m
x
+
y
m
+
1
x
+
m
y
2
. Khi m a thì hệ có vô số nghiệm và khi m b thì hệ vô nghiệm. Tính a+ b? A. 0 B.1...
Đọc tiếp
Cho hệ phương trình có tham số m: m x + y = m + 1 x + m y = 2 . Khi m =a thì hệ có vô số nghiệm và khi m = b thì hệ vô nghiệm. Tính a+ b?
A. 0
B.1
C. -1
D. 2
Ta tính các định thức:
D = m 1 1 m = m 2 - 1 = m + 1 . m - 1 ; D x = m + 1 1 2 m = m 2 + m - 2 = m - 1 . m + 2 ; D y = m m + 1 1 2 = m - 1
Xét D = 0 tức là m = 1 hoặc m = -1.
* Nếu m = 1 thì D = Dx = Dy = 0 nên hệ phương trình đã cho có vô số nghiệm.
Do đó, a= 1.
* Nếu m = -1 thì D = 0 nhưng D x ≠ 0 nên hệ phương trình đã cho vô nghiệm.
Do đó, b = -1
Tổng a+ b = 0.
Chọn A.
Đúng 0
Bình luận (0)
1, Cho hai tập hợp: A=[2m-1;+∞) ; B=(-∞;m+3] . A giao B ≠ ∅ khi và chỉ khi
A.m≤4 B.m≥3 C.m≥-4 D.m≥4
2. Cho hai tập hợp: A=[m;m+2] ;B=[2m-1;2m+3] . A giao B ≠ ∅ khi và chỉ khi
A. -3<m<3 B.-3<m≤3 C.-3≤m<3 D.-3≤m≤3
( Các bạn giải ra cụ thể giúp mình vs)
M=\(\left(\frac{1}{a}+\frac{a}{a+1}\right):\frac{a}{a^2+a}\)
a) Rút gọn biểu thức M
b) Tính giá trị của M khi (a-5)(a+1)=0
c) Tìm giá trị nhỏ nhất của M khi a>0
Biết rằng phương trình
5
2
x
+
1
-
2
x
-
m
.
5
1
-
1
-
2
x
4
.
5
x
có nghiệm khi và chỉ khi m ∈ [a;b], với m là tham số. Giá trị của b - a bằng...
Đọc tiếp
Biết rằng phương trình 5 2 x + 1 - 2 x - m . 5 1 - 1 - 2 x = 4 . 5 x có nghiệm khi và chỉ khi m ∈ [a;b], với m là tham số. Giá trị của b - a bằng
A. 9 5
B. 9
C. 1 5
D. 1
So sánh số hữu tỉ a/b (a,b,m thuộc Z,m > 0) với số 0 khi a, b cùng dấu và khi a,b khác dấu
đường thẳng (d1) \(y=x-2\)và (d2) \(y=2x+m\) cách nhau tại một điểm khi và chỉ khi
A. m=2
B. m≠2
C. m=-2
D. m=+-2
Giải các phương trình sau: a)
3
m
m
+
1
−
3
x
−
2
0
khi
m
1
2
;b)
m
2...
Đọc tiếp
Giải các phương trình sau:
a) 3 m m + 1 − 3 x − 2 = 0 khi m = 1 2 ;
b) m 2 + 10 m + 25 x = m − 2 5 khi m = - 3 .
a) Tìm được x = - 1 b) Tìm được x = 17 20
Đúng 0
Bình luận (0)
cho biểu thức ;
A= 18 nhân 75 + 9 nhân m nhân 2 / 45 nhân 10 + 9 nhân 8 nhân 5
a, tính A khi m = 60
b tính m khi A = 6
Giải các phương trình sau:a)
−
16
+
8
m
−
m
2
x
−
2
m
2
+
11
0
khi m 5.b)
x
m
2
2...
Đọc tiếp
Giải các phương trình sau:
a) − 16 + 8 m − m 2 x − 2 m 2 + 11 = 0 khi m = 5.
b) x m 2 2 m 2 − 1 − m = 2 m x + 1 khi m = 1.