Tìm các tiệm cận của mỗi đồ thị hàm số sau:
a) \(y = \frac{{3x - 2}}{{x + 1}}\);
b) \(y = \frac{{{x^2} + 2x - 1}}{{2x - 1}}\).
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
QL
Những câu hỏi liên quan
Nêu cách tìm ra tiệm cận ngang và tiệm cận dứng của đồ thị hàm số. Áp dụng để tìm các tiệm cận của đồ thị hàm số: Áp dụng để tìm các tiệm cận của đồ thị hàm số y = 2 x + 3 2 - x
- Cách tìm tiệm cận ngang:
+ Tính các giới hạn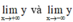 
+ Nếu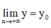 
hoặc 
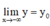thì
y
=
y
o
là tiệm cận ngang của đồ thị hàm số.
- Cách tìm tiệm cận đứng:
Đường thẳng x = x o là tiệm cận đứng của đồ thị hàm số y = f(x) nếu ít nhất một trong các điều kiện sau được thỏa mãn:
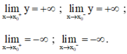
Đúng 0
Bình luận (0)
Gọi số
n
∈
N
là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
x
+
1
x
2
-
3
x
+
2
. Tìm n A.1 B.0 C. 2 D. 3
Đọc tiếp
Gọi số n ∈ N là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x + 1 x 2 - 3 x + 2 . Tìm n
A.1
B.0
C. 2
D. 3
26. Tìm số đường tiệm cận ngang và số đường tiệm cận đứng của đồ thị hàm số y = \(\dfrac{\sqrt{x-1}}{x^2-3x+2}\)
\(\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow+\infty}\dfrac{\sqrt{\dfrac{1}{x^3}-\dfrac{1}{x^4}}}{1-\dfrac{3}{x}+\dfrac{2}{x^2}}=0\)
\(\Rightarrow y=0\) là tiệm cận ngang
\(\lim\limits_{x\rightarrow1^+}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\lim\limits_{x\rightarrow1^+}\dfrac{1}{\sqrt{x-1}\left(x-2\right)}=\infty\)
\(\Rightarrow x=1\) là tiệm cận đứng
\(\lim\limits_{x\rightarrow2}\dfrac{\sqrt{x-1}}{x^2-3x+2}=\dfrac{1}{0}=\infty\)
\(\Rightarrow x=2\) là tiệm cận đứng
ĐTHS có 1 TCN và 2 TCĐ
Đúng 1
Bình luận (0)
Tìm các tiệm cận đứng và ngang của đồ thị mỗi hàm số sau:
y
3
x
+
x
2
+
1
2
+
3
x
2
+
2
Đọc tiếp
Tìm các tiệm cận đứng và ngang của đồ thị mỗi hàm số sau: y = 3 x + x 2 + 1 2 + 3 x 2 + 2
TXĐ: R.
Từ
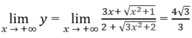
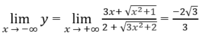
Ruy ra đồ thị hàm số có các tiệm cận ngang:
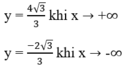
Đồ thị hàm số không có tiệm cận đứng.
Đúng 0
Bình luận (0)
Gọi số n thuộc N là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số
y
x
+
1
x
2
-
3
x
+
2
Tìm n A.1 B.0 C. 2 D. 3
Đọc tiếp
Gọi số n thuộc N là tổng các đường tiệm cận ngang và tiệm cận đứng của đồ thị hàm số y = x + 1 x 2 - 3 x + 2 Tìm n
A.1
B.0
C. 2
D. 3
Tìm các tiệm cận đường và ngang của đồ thị mỗi hàm số sau: y = 5 2 - 3 x
Vì
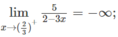
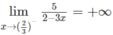
nên x = 2/3 là tiệm cận đứng.
Do
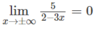
nên y = 0 là tiệm cận ngang.
Đúng 0
Bình luận (0)
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số
y
3
x
-
1
x
-
2
A. x 2 B. x 3 C. y 3 D. y 2
Đọc tiếp
Tìm phương trình đường tiệm cận ngang của đồ thị hàm số y = 3 x - 1 x - 2
A. x = 2
B. x = 3
C. y = 3
D. y = 2
Tìm các đường tiệm cận của đồ thị hàm số
y
3
x
+
2
x
+
2
. A.
x
−
2
v
à
x
3
B.
y
3
v
à
x...
Đọc tiếp
Tìm các đường tiệm cận của đồ thị hàm số y = 3 x + 2 x + 2 .
A. x = − 2 v à x = 3
B. y = 3 v à x = 2
C. y = − 3 v à x = − 2
D. x = − 2 v à y = − 3
Đáp án C
Ta có: lim x → 2 − y = lim x → 2 − 3 x + 2 x + 2 = − ∞ và lim x → 2 + y = lim x → 2 + 3 x + 2 x + 2 = + ∞ nên đường thẳng x = − 2 là tiệm cận đứng của đồ thị hàm số đã cho.
Ta có: lim x → − ∞ y = lim x → − ∞ 3 x + 2 x + 2 = lim x → − ∞ 3 x + 2 x x + 2 x = lim x → − ∞ 3 + 2 x x x + 2 x = 3 − 1 = − 3 nên đường thẳng y = − 3 là tiệm cận ngang của đồ thị hàm số đã cho.
Ta có: lim x → + ∞ y = lim x → + ∞ 3 x + 2 x + 2 = lim x → + ∞ 3 x + 2 x x + 2 x = lim x → + ∞ 3 + 2 x x x + 2 x = 3 1 = 3 nên đường thẳng y = 3 là tiệm cận ngang của đồ thị hàm số đã cho.
Đúng 0
Bình luận (0)
Tìm tiệm cận đứng của đồ thị hàm số
y
3
x
+
2
2
x
+
1
-
x
A.
x
1
-
2
B.
x
1
±
2
C.
x
1...
Đọc tiếp
Tìm tiệm cận đứng của đồ thị hàm số y = 3 x + 2 2 x + 1 - x
A. x = 1 - 2
B. x = 1 ± 2
C. x = 1 + 2
D. x = - 1 2
Tìm tiệm cận ngang của đồ thị hàm số
y
x
+
x
2
−
3
x
+
1
A.
y
3
2
B. (C) không có tiệm cận ngang C. y 3 D. ...
Đọc tiếp
Tìm tiệm cận ngang của đồ thị hàm số y = x + x 2 − 3 x + 1
A. y = 3 2
B. (C) không có tiệm cận ngang
C. y = 3
D. y = − 3 2
Đáp án A
Bằng cách áp dụng công thức tìm tiệm cận,
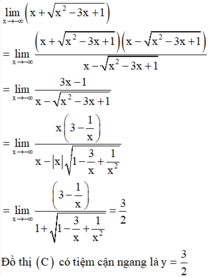
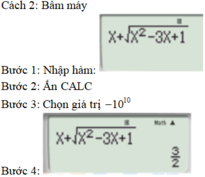
Lỗi sai
* Học sinh thường mắc sai lầm lim x → + ∞ x + x 2 − 3 x + 1 = + ∞
Và kết luận hàm số không có tiệm cận ngang, nên sai lầm chọn đáp án B
Đúng 0
Bình luận (0)