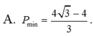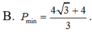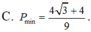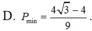Xét các số thực x;y;z thỏa mãn \(x\left(x-1\right)+y\left(y-1\right)+z\left(z-1\right)\le\frac{3}{4}\)
Tìm GTNN ;GTLN của biểu thức P=x+y+z
DN
Những câu hỏi liên quan
Với mỗi số thực x, xét các mệnh đề P: “ x 2 = 1”, Q: “x = 1”
Mệnh đề đảo “Nếu x = 1 thì x 2 thì x =1” là đúng.
Đúng 0
Bình luận (0)
Cho R là nhóm cộng các số thực và R* là nhóm nhân các số thực dương. Xét xem ánh xạ f: R ® R* được xác định bởi f(x) = 5x có phải là một đồng cấu từ nhóm cộng các số thực vào nhóm nhân các số thực dương không?
bằng còn cái nịt
Cho R là nhóm cộng các số thực và R* là nhóm nhân các số thực dương. Xét xem ánh xạ f: R ® R* được xác định bởi f(x) = 5x có phải là một đồng cấu từ nhóm cộng các số thực vào nhóm nhân các số thực dương không?
Xét các số thực dương x , y thỏa mãn x + y ≤ 1 . Chứng minh rằng x + y + 1/x + 1/y ≥ 5
Ta có:
Đặt \(A=x+y+\dfrac{1}{x}+\dfrac{1}{y}\)
\(\Leftrightarrow A=x+y+\dfrac{4}{4x}+\dfrac{4}{4y}\)
\(\Leftrightarrow A=x+y+\dfrac{1}{4x}+\dfrac{3}{4x}+\dfrac{1}{4y}+\dfrac{3}{4y}\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{4x}\right)+\left(y+\dfrac{1}{4y}\right)+\left(\dfrac{3}{4x}+\dfrac{3}{4y}\right)\)
\(\Rightarrow A\ge2\sqrt{x.\dfrac{1}{4x}}+2\sqrt{y.\dfrac{1}{4y}}+\dfrac{3}{4}.\dfrac{4}{x+y}\)
\(\ge2.\sqrt{\dfrac{1}{4}}+2\sqrt{\dfrac{1}{4}}+\dfrac{3}{4}.\dfrac{4}{1}\)
\(=2.\dfrac{1}{2}+2.\dfrac{1}{2}+3=1+1+3=5\)
Vậy ta có đpcm. Dấu"=" xảy ra\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{1}{4x}\\y=\dfrac{1}{4y}\\x=y\\x+y=1\end{matrix}\right.\) \(\Leftrightarrow x=y=\dfrac{1}{2}\left(tm\right)\)
Đúng 3
Bình luận (0)
Xét các số thực xba0. Cho hàm số yf(x) có đạo hàm liên tục trên R và có bảng xét dấu của đạo hàm như hình vẽ. Đặt
g
x
f
x
3
Số điểm cực trị của hàm số yg(x) là A. 3 B. 7 C. 4 D. 5
Đọc tiếp
Xét các số thực x>b>a>0. Cho hàm số y=f(x) có đạo hàm liên tục trên R và có bảng xét dấu của đạo hàm như hình vẽ. Đặt g x = f x 3 Số điểm cực trị của hàm số y=g(x) là
A. 3
B. 7
C. 4
D. 5
Xét các số thực dương x,y thoả mãn điều kiện x3 + y3 +(x + y)3 + 30xy = 2000. Chứng minh rằng x +y =10
\(\Leftrightarrow\left(x+y\right)^3-3xy\left(x+y\right)+\left(x+y\right)^3+30xy=2000\)
\(\Leftrightarrow2\left[\left(x+y\right)^3-1000\right]-3xy\left(x+y-10\right)=0\)
\(\Leftrightarrow2\left(x+y-10\right)\left[\left(x+y\right)^2-10\left(x+y\right)+100\right]-3xy\left(x+y-10\right)=0\)
\(\Leftrightarrow\left(x+y-10\right)\left[2\left(x+y\right)^2-20\left(x+y\right)+200-3xy\right]=0\)
\(\Leftrightarrow x+y=10\)
Do:
\(2\left(x+y\right)^2-20\left(x+y\right)+200-3xy\)
\(=\left(x+y-10\right)^2+\left(x+y\right)^2-3xy+100\)
\(=\left(x+y-10\right)^2+\left(x+\dfrac{y}{2}\right)^2+\dfrac{3y^2}{4}+100>0\)
Đúng 2
Bình luận (1)
Xét các số thực dương x , y , z thỏa mãn x + y + z ≤ 1 . Chứng minh rằng x + y + z + 1/x + 1/y + 1/z ≥ 10 .
Đặt \(A=x+y+z+\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\)
\(\Leftrightarrow A=x+y+z+\dfrac{9}{9x}+\dfrac{9}{9y}+\dfrac{9}{9z}\)
\(\Leftrightarrow A=x+y+z+\dfrac{1}{9x}+\dfrac{8}{9x}+\dfrac{1}{9y}+\dfrac{8}{9y}+\dfrac{1}{9z}+\dfrac{8}{9z}\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{9x}\right)+\left(y+\dfrac{1}{9y}\right)+\left(z+\dfrac{1}{9z}\right)+\left(\dfrac{8}{9x}+\dfrac{8}{9y}+\dfrac{8}{9z}\right)\)
\(\Leftrightarrow A=\left(x+\dfrac{1}{9x}\right)+\left(y+\dfrac{1}{9y}\right)+\left(z+\dfrac{1}{9z}\right)+\dfrac{8}{9}.\left(\dfrac{1^2}{x}+\dfrac{1^2}{y}+\dfrac{1^2}{z}\right)\)
\(\Rightarrow A\ge2\sqrt{x.\dfrac{1}{9x}}+2\sqrt{y.\dfrac{1}{9y}}+2\sqrt{z.\dfrac{1}{9z}}+\dfrac{8}{9}.\dfrac{\left(1+1+1\right)^2}{x+y+z}\)
\(\Rightarrow A\ge2\sqrt{\dfrac{1}{9}}+2\sqrt{\dfrac{1}{9}}+2\sqrt{\dfrac{1}{9}}+\dfrac{8}{9}.\dfrac{3^2}{1}\)
\(\Rightarrow A\ge2.\dfrac{1}{3}.3+8=2+8=10\)
Vậy ta có BĐT cần chứng minh.
Dấu\("="\) xảy ra\(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
Xét các số thực dương thỏa mãn
log
3
1
-
x
y
x
+
2
y
3
x
y
+
x
+
2
y
-
4
. Tìm giá trị nhỏ nhất Smin của S x + y A.
S
m
i...
Đọc tiếp
Xét các số thực dương thỏa mãn log 3 1 - x y x + 2 y = 3 x y + x + 2 y - 4 . Tìm giá trị nhỏ nhất Smin của S = x + y
A. S m i n = 9 11 9 - 1
B. S m i n = 9 11 - 9 9
C. S m i n = 2 11 - 9 9
D. Đáp án khác
Xét các số thực dương x, y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P
m
i
n...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
A. P m i n = 4 3 + 4 3
B. P m i n = 4 3 - 4 3
C. P m i n = 4 3 - 4 9
D. P m i n = 4 3 + 4 9
Xét các số thực dương x, y thỏa mãn
log
3
1
-
y
x
+
3
x
y
3
x
y
+
x
+
3
y
-
4
. Tìm giá trị nhỏ nhất
P
m
i
n...
Đọc tiếp
Xét các số thực dương x, y thỏa mãn log 3 1 - y x + 3 x y = 3 x y + x + 3 y - 4 . Tìm giá trị nhỏ nhất P m i n của P = x + y
