Cho ∆ABC có 3 góc nhọn cắt đường cao AD;BE;CF cắt nhau tại H a) C/m ∆AEB đồng dạng ∆AFC b) C/m AH.CD=HE.AC
H24
Những câu hỏi liên quan
Cho tam giác ABC có 3 góc nhọn, nội tiếp đường tròn O. Hai đường cao AD, BE cắt nhau tại H. Chứng minh tứ giác ABDE nội tiếp đường tròn
Cho tam giác ABC có 3 gó nhọn , nội tiếp đường tròn O . Hai đường cao AD,BE cắt nhau tại H
a, chứng minh tứ giác ABDE nội tiếp đường tròn
b, Tia AO cắt đương tròn O tại K . Chứng minh tứ giác BHCK là hình bình hành
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O;R) (AB
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn (O;R) (AB<AC) 3 đường cao AD,BE,CF cắt nhau tại H
a,CM tứ giác BFEC nội tiếp và xác định tâm I
b,Đường thẳng EF cắt đường thẳng BC tại K . CM KF.KE=KB.KC
c,AK cắt (O) tại M. CM MFEA nội tiếp
jup mình vs ạ
Bài 10: Cho ABC nhọn có các đường cao AE, CD cắt nhau tại H (E BC, D AB).a) Chứng minh: ABE ∽ CBD b) Chứng minh: HD . HC HA.HE c) Nếu BD 3cm, DC 4cm. Tính tỉ số AHDHBài 11: Cho tam giác ABC có 3 góc nhọn, các đường cao AD, BE, CF cắt nhau tại H. a) Cm: ABE và ACF đồng dạng. b) Cm: HE.HB HC.HF c) Cm: góc AEF bằng góc ABC. d) Cm: EB là tia phân giác của góc DEF.
Đọc tiếp
Bài 10: Cho ABC nhọn có các đường cao AE, CD cắt nhau tại H (E BC, D AB).
a) Chứng minh: ABE ∽ CBD b) Chứng minh: HD . HC = HA.HE c) Nếu BD = 3cm, DC = 4cm. Tính tỉ số AH
DH
Bài 11: Cho tam giác ABC có 3 góc nhọn, các đường cao AD, BE, CF cắt nhau tại H. a) Cm: ABE và ACF đồng dạng. b) Cm: HE.HB = HC.HF c) Cm: góc AEF bằng góc ABC. d) Cm: EB là tia phân giác của góc DEF.
Bài 10:
a) Xét ΔABE vuông tại E và ΔCBD vuông tại D có
\(\widehat{DBC}\) chung
Do đó: ΔABE\(\sim\)ΔCBD(g-g)
b) Xét ΔHDA vuông tại D và ΔHEC vuông tại E có
\(\widehat{AHD}=\widehat{CHE}\)(hai góc đối đỉnh)
Do đó: ΔHDA\(\sim\)ΔHEC(g-g)
Suy ra: \(\dfrac{HD}{HE}=\dfrac{HA}{HC}\)
hay \(HD\cdot HC=HE\cdot HA\)
Đúng 2
Bình luận (1)
Bài 11:
a) Xét ΔABE vuông tại E và ΔACF vuông tại F có
\(\widehat{FAC}\) chung
Do đó: ΔABE\(\sim\)ΔACF(g-g)
b) Xét ΔFHB vuông tại F và ΔEHC vuông tại E có
\(\widehat{FHB}=\widehat{EHC}\)(hai góc đối đỉnh)
Do đó: ΔFHB\(\sim\)ΔEHC(g-g)
Suy ra: \(\dfrac{HF}{HE}=\dfrac{HB}{HC}\)
hay \(HE\cdot HB=HF\cdot HC\)
c) Ta có: ΔAEB\(\sim\)ΔAFC(cmt)
nên \(\dfrac{AE}{AF}=\dfrac{AB}{AC}\)
hay \(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)
Xét ΔAEF và ΔABC có
\(\dfrac{AE}{AB}=\dfrac{AF}{AC}\)(cmt)
\(\widehat{FAE}\) chung
Do đó: ΔAEF\(\sim\)ΔABC(c-g-c)
Suy ra: \(\widehat{AEF}=\widehat{ABC}\)
Đúng 1
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn, 3 đường cao AD, BE, CF cắt nhau tại H. CMR: HD/AH + HE/BE + HF/CF = 1
Xem chi tiết
a,Xét tg DHB và tg DCA có: ^HDB=^CDA=90 độ, ^DBH=^DAC ( cùng phụ với hai góc bằng nhau BHD=^AHE)
Do đó: tg HDB đồng dạng tg DCA (g.g)
Suy ra: HD/DC=BD/DA-> bd*dc=dh*da
b, HD/HA=SBHC/SABC
HE/BE=SAHC/SABC
HF/CF=SHAB/SABC
HD/HA+HE/BE+HF/CF=SBHC/SABC+SAHC/SABC+SAHB/SABC=1
Cho tam giác ABC có 3 góc nhọn nội tiếp đường tròn O(AB<AC) có 3 đường cao AD,BE,CF cắt nhau tại H. EF cắt BC tại M và cắt AD tại I, AM cắt (O) tại N. Chứng minh NI là phân giác của góc END.
Cho tam giác ABC có ba góc nhọn. Vẽ đường cao AD, BE, CF cắt nhau tại H
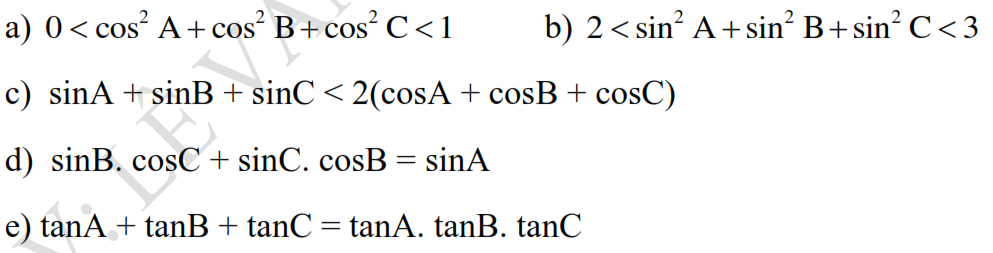
Cho tam giác ABC có 3 góc nhọn, 3 đường cao AD, BE, CF cắt nhau tại H. Cho BD=2cm, DC=3cm, Sabc=30cm2. Tính Shbc
Ta có: S \(\Delta\)ABC =\(\frac{AD\cdot BC}{2}\)
Hay 30 =\(\frac{AD\cdot5}{2}\)
=> AD =12 (cm)
Mặt khác: \(\widehat{HBD}\)+\(\widehat{BHD}\)=90 (\(\Delta\)BHD vuông tại D)
\(\widehat{DAC}\)+\(\widehat{AHE}\)=90 (\(\Delta\)AHE vuông tại E)
Mà: \(\widehat{BHD}\)=\(\widehat{AHE}\)( 2 góc đối đỉnh )
=> \(\widehat{HBD}\)=\(\widehat{DAC}\)
Xét \(\Delta\)BHD và \(\Delta\)ADC có:
\(\widehat{BDH}\)= \(\widehat{ADC}\) ( = 90*)
\(\widehat{HBD}\)= \(\widehat{DAC}\)( cmt )
=> \(\Delta BHD\)đồng dạng với \(\Delta ACD\)( g-g )
=> \(\frac{BD}{AD}=\frac{HD}{CD}\)
=> BD.CD = AD.HD
=> 6 = 12.HD
=> HD = 1/2 (cm)
Vậy S\(\Delta BHC\)=\(\frac{BC\cdot HD}{2}\)=\(\frac{5\cdot0,5}{2}\)=1,25 (cm2)
Đúng 0
Bình luận (0)
Cho Tam giác ABC có 3 góc nhọn nội tiếp đường tròn tâm o . Hai đường cao AD, BE cắt nhau tại H . Chứng minh DB. DC = DH . DA
Bài 4: Cho ABC có 3 góc nhọn (AB<AC) có 3 đường cao. AD, BE, CF cắt nhau tại Ha/ c/m:AHFᔕABDb/ c/m:AHBᔕAFDgiúp giải bài, xin cảm ơn.
Xem chi tiết
a: Xét ΔAHF vuông tại F và ΔABD vuông tại D có
góc HAF chung
=>ΔAHF đồng dạng vơi ΔABD
=>AH/AB=AF/AD
=>AH/AF=AB/AD
b: Xét ΔAHB và ΔAFD có
AH/AF=AB/AD
góc HAB chung
=>ΔAHB đồng dạng với ΔAFD
Đúng 0
Bình luận (1)



 đó nha bn
đó nha bn