Bạn làm theo cách này nhé, sẽ ngắn gọn hơn !

Hạ đường cao AH của \(\Delta\)ABC.

Ta có: ^ADH là góc ngoài của \(\Delta\)ADB => ^ADH = ^ABD + ^BAD = 30⁰ + 15⁰ = 45⁰

Xét \(\Delta\)AHD có: ^AHD=90⁰; ^ADH=45⁰ => \(\Delta\)AHD vuông cân tại H => HD = AH. 

Dễ thấy: \(\Delta\)AHB là tam giác nửa đều => AH=1/2.AB => HD=1/2.AB

\(\Delta\)AHC cũng là tam giác nửa đều => HC=1/2.AC

=> HD + HC = 1/2 (AB+AC) => CD = (AB+AC)/2

=> AC + CD = AC +  (AB+AC)/2. Do \(\Delta\)ABC nửa đều => AC=BC/2

=> AC + CD = BC/2 + (AB+AC)/2 = C_ABC/2 (đpcm).

Qua D kẻ đường thẳng vuông góc với BC cắt tia CA tại E. DE giao AB ở I

Gọi H và K lần lượt là hình chiếu của A lên CD và DE

Xét \(\Delta\)BID và \(\Delta\)AIE: ^BDI = ^EAI = 90⁰; ^BID = ^AIE (Đối đỉnh)

=> ^DBI = ^AEI hay ^HBA = ^KEA

Ta có: ^HAB + ^HBA =90⁰; ^KAE + ^KEA = 90⁰. Mà ^HBA=^KEA => ^HAB = ^KAE.

Ta thấy: ^ADC là góc ngoài \(\Delta\)BAD => ^ADC = ^BAD + ^ABD = 30⁰ + 15⁰ = 45⁰

Mà ^CDE = 90⁰ = .^CDE= 2.^ADC => DA là phân giác ^CDE

Do H và K là hình chiếu của A lên CD và DE => AH=AK (T/c đường phân giác)

Xét \(\Delta\)AHB và \(\Delta\)AKE: AH=AK; ^AHB = ^AKE =90⁰; ^HAB = ^KAE (cmt)

=> \(\Delta\)AHB = \(\Delta\)AKE (g.c.g)  => AB=AE (2 cạnh tương ứng)

Xét \(\Delta\)CDE: ^CDE=90⁰; ^DCE=60⁰ => \(\Delta\)CDE là tam giác nửa đều

= > \(CD=\frac{CE}{2}=\frac{AC+AE}{2}=\frac{AB+AC}{2}\)(Do AB=AE)

\(\Leftrightarrow AC+CD=AC+\frac{AB+AC}{2}\)(1)

Mặt khác \(\Delta\)ABC là tam giác nửa đều => \(AC=\frac{BC}{2}\)(2)

Từ (1) và (2) \(\Rightarrow AC+CD=\frac{BC}{2}+\frac{AB+AC}{2}=\frac{AB+AC+BC}{2}=\frac{C_{\Delta ABC}}{2}\)

=> ĐPCM.

Kurokawa Neko làm đúng hết rồi. ^~^

B

Chọn A

chọn đáp án B

Bài 2:

Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)và\(AH\perp BC\)

\(\Rightarrow AH^2=HB.HC\)(Hệ thức lượng)

\(AH^2=25.64\)

\(AH=\sqrt{1600}=40cm\)

Xét \(\Delta ABH\)có\(\widehat{H}=90^o\)

\(\Rightarrow\tan B=\frac{AH}{BH}\)\(=\frac{40}{25}=\frac{8}{5}\)

\(\Rightarrow\widehat{B}\approx58^o\)

Xét \(\Delta ABC\)có \(\widehat{A}=90^o\)

\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)

\(58^o+\widehat{C}=90^o\)

\(\Rightarrow\widehat{C}\approx90^o-58^o\)

\(\widehat{C}\approx32^o\)

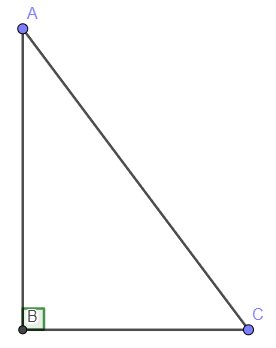
a, \(sin\left(A\right)=\dfrac{BC}{AC}\Leftrightarrow sin\left(40^o\right)=\dfrac{BC}{8}\Leftrightarrow BC\approx5,14\left(cm\right)\)
\(cos\left(A\right)=\dfrac{AB}{AC}\Leftrightarrow cos\left(40^o\right)=\dfrac{AB}{8}\Leftrightarrow AB\approx6,12\left(cm\right)\)
b,
\(cotg\left(C\right)=\dfrac{BC}{AB}\Leftrightarrow\dfrac{1}{\sqrt{3}}=\dfrac{BC}{5}\Leftrightarrow BC=\dfrac{5\sqrt{3}}{3}\left(cm\right)\)
\(AC^2=AB^2+BC^2\Leftrightarrow AC=\sqrt{AB^2+BC^2}=\sqrt{5^2+\left(\dfrac{5\sqrt{3}}{3}\right)^2}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)

Kẻ D sao cho A là trung điểm của CD . Tam giác BCD có đường cao BA (gt) và trung tuyến BA nên tam giác BDC cân ở B mà có góc C = 60 độ ( C= 90 - B= 90-30= 60)
Do đó tam giác BDC đều nên BC = CD mà AC= 1/2 CD( A là tđ CD) nên AC= 1/2 BC (đpcm)

Với tam giác ABC có góc A = 90 o và góc B = 30 o => góc C = 60 o Gọi M là trung điểm của BC mà Δ ABC có góc A = 90 o =>AM=BM=CM(định lý) =>tam giác AMC cân tại M mà góc C = 60 o => Δ AMC đều =>AC=MC mà MC =1/2.BC => AC = 1/2 BC

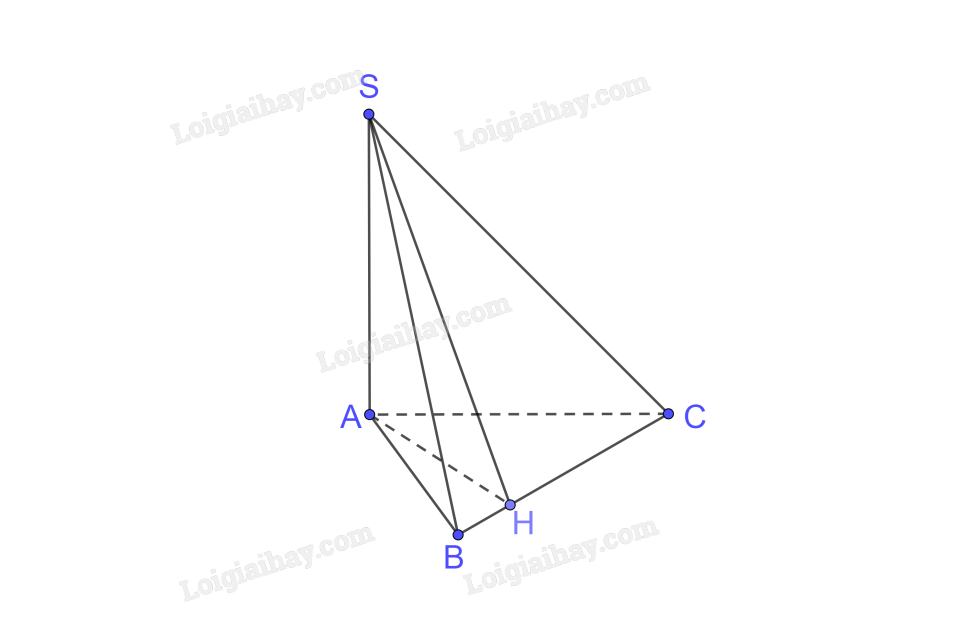
a) \(SA \bot \left( {ABC} \right);SA \subset \left( {SAB} \right) \Rightarrow \left( {SAB} \right) \bot \left( {ABC} \right)\)

\(\left. \begin{array}{l}AH \bot BC\\SA \bot BC\left( {SA \bot \left( {ABC} \right)} \right)\\AH \cap SA = \left\{ A \right\}\end{array} \right\} \Rightarrow BC \bot \left( {SAH} \right);BC \subset \left( {SBC} \right) \Rightarrow \left( {SAH} \right) \bot \left( {SBC} \right)\)

b) Ta có \(AH \bot BC,BC \bot SH\left( {BC \bot \left( {SAH} \right)} \right)\)

\( \Rightarrow \left[ {S,BC,A} \right] = \left( {SH,AH} \right) = \widehat {SHA}\)

Xét tam giác ABC vuông tại A có

\(\widehat {ABC} = {30^0} \Rightarrow \widehat {ACH} = {60^0}\)

Xét tam giác ACH vuông tại H có

\(\sin \widehat {ACH} = \frac{{AH}}{{AC}} \Rightarrow AH = a.\sin {60^0} = \frac{{a\sqrt 3 }}{2}\)

Xét tam giác SHA vuông tại A có

\(\tan \widehat {SHA} = \frac{{SA}}{{AH}} = \frac{{a\sqrt 3 }}{2}:\frac{{a\sqrt 3 }}{2} = 1 \Rightarrow \widehat {SHA} = {45^0}\)

Vậy \(\left[ {S,BC,A} \right] = {45^0}\)

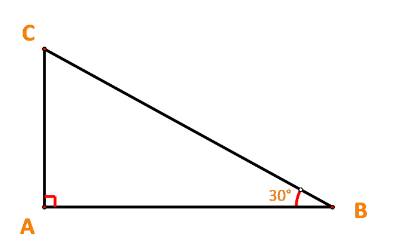
Ta có: \(BC = \frac{{AB}}{{\cos {{30}^o}}} = 3:\frac{{\sqrt 3 }}{2} = 2\sqrt 3 \); \(AC = BC.\sin \widehat {ABC} = 2\sqrt 3 .\sin {30^o} = \sqrt 3 .\)

\(\overrightarrow {BA} .\overrightarrow {BC}  = \left| {\overrightarrow {BA} } \right|.\left| {\overrightarrow {BC} } \right|\cos (\overrightarrow {BA} ,\overrightarrow {BC} ) = 3.2\sqrt 3 .\cos \widehat {ABC} = 6\sqrt 3 .\cos {30^o} = 6\sqrt 3 .\frac{{\sqrt 3 }}{2} = 9.\)

\(\overrightarrow {CA} .\overrightarrow {CB}  = \left| {\overrightarrow {CA} } \right|.\left| {\overrightarrow {CB} } \right|\cos (\overrightarrow {CA} ,\overrightarrow {CB} ) = \sqrt 3 .2\sqrt 3 .\cos \widehat {ACB} = 6.\cos {60^o} = 6.\frac{1}{2} = 3.\)

Mik xem zồi trên google có đó bn lên đó xem nha!

Với tam giác ABC có góc A = \(90^o\)và góc B = \(30^o\)

=> Góc C = \(60^o\)

Gọi M là trung điểm của BC

Mà \(\Delta ABC\)có góc A = 90\(^o\)

=> AM = BM = CM       \((\)định lý \()\)

=> Tam giác AMC cân tại M

Mà góc C = 60\(^o\)

=> \(\Delta ABC\)đều

=> AM = MC

Mà MC = \(\frac{1}{2}\)BC

Vậy : \(AC=\frac{1}{2}BC\)

Mình xin lỗi bạn tự nhiên mk chứng minh \(AC=\frac{1}{2}BC\)

Sorry bạn