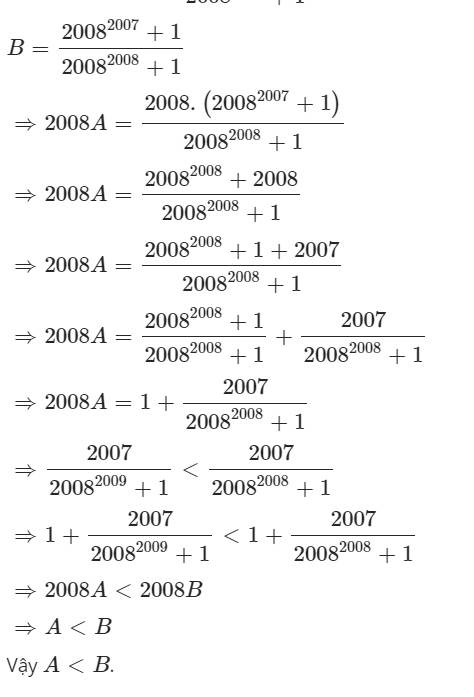
So sánh bt: \(A=\dfrac{2008^{2008}+1}{2008^{2009}+1};B=\dfrac{2008^{2007}+1}{2008^{2008}+1}\)
ND
Những câu hỏi liên quan
So sánh A và B biết: A= \(\dfrac{2008+2008+2010}{2009+2010+2011}\) và B= \(\dfrac{2008}{2009}\)+ \(\dfrac{2009}{2010}\)+ \(\dfrac{2010}{2011}\)
A = \(\dfrac{2008}{2009+2010+2011}+\dfrac{2009}{2009+2010+2011}+\dfrac{2010}{2009+2010+2011}\)
Ta có:
\(\dfrac{2008}{2009}>\dfrac{2008}{2009+2010+2011}\)
\(\dfrac{2009}{2010}>\dfrac{2009}{2009+2010+2011}\)
\(\dfrac{2010}{2011}>\dfrac{2010}{2009+2010+2011}\)
Từ 3 điều trên suy ra : A < B
Đúng 2
Bình luận (0)
So sánh :A=2008^2008 +1 /2008^2009 B =2008^2007 +1 /2008^2008+1
So sánh: A=2008^2008+1/2008^2009+1 và B = 2008^2007+1/2008^2008+1
Bài này hơi dài nên bạn bấn vào đây để xem lời giải Giúp tôi giải toán - Hỏi đáp, thảo luận về toán học - Học toán với OnlineMath
Đúng 0
Bình luận (0)
So sánh \(A=\dfrac{2008^{2009}+2}{2008^{2009}-1};B=\dfrac{2008^{2009}}{2008^{2009}-3}\)
ta có: \(A=\dfrac{2008^{2009}+2}{2008^{2009}-1}=\dfrac{2008^{2009}-1+3}{2008^{2009}-1}=1+\dfrac{3}{2008^{2009}-1}\)
B=\(\dfrac{2008^{2009}}{2008^{2009}-3}=\dfrac{2008^{2009}-3+3}{2008^{2009}-3}=1+\dfrac{3}{2008^{2009}-3}\)
ta thấy: \(1+\dfrac{3}{2008^{2009}-1}\)<\(1+\dfrac{3}{2008^{2009}-3}\)
vậy A<B
Đúng 0
Bình luận (0)
So sánh
(2008^2009+1)/ (2008^2009-1) và (2008^2009)/ (2008^2009-3)
Câu 19. Cho ${A}=\dfrac{2008^{2008}+1}{2008^{2009}+1}$; ${B}=\dfrac{2008^{2007}+1}{2008^{2008}+1}$. So sánh $A$ và $B$.
Xem thêm câu trả lời
so sánh 2008^2008+1 / 2008^2009+1 và 2008^2007+1 / 2008^2008+1
ta có Đặt \(A=\frac{2008^{2008}+1}{2008^{2009}+1}\)
\(B=\frac{2008^{2007}+1}{2008^{2008}+1}\)
Xét A trước ta có
\(2008A=\frac{2008\left(2008^{2008}+1\right)}{2008^{2009}+1}\)\(2008A=\frac{2008^{2009}+2008}{2008^{2009}+1}\)
\(2008A=\frac{2008^{2009}+1+2007}{2008^{2009}+1}\)suy ra \(2008A=1+\frac{2007}{2008^{2009}+1}\)
Xét B ta có
\(2008B=\frac{2008.\left(2008^{2007}+1\right)}{2008^{2008}+1}\)suy ra \(2008B=\frac{2008^{2008}+2008}{2008^{2008}+1}\)
\(2008B=\frac{2008^{2008}+1+2007}{2008^{2008}+1}\)suy ra \(2008B=1+\frac{2007}{2008^{2008}+1}\)
VÌ \(1+\frac{2007}{2008^{2009}+1}
Đúng 2
Bình luận (0)
Đặt \(a=2008^{2007};\)
\(A=\frac{2008^{2008}+1}{2008^{2009}+1}=\frac{2008a+1}{2008^2.a+1};\text{ }B=\frac{2008^{2007}+1}{2008^{2008}+1}=\frac{a+1}{2008a+1}\)
Quy đồng mẫu ta có:
\(A=\frac{\left(2008a+1\right)\left(2008a+1\right)}{\left(2008^2a+1\right)\left(2008a+1\right)}=\frac{2008^2a^2+2.2008a+1}{\left(2008^2a+1\right)\left(2008a+1\right)}\)
\(B=\frac{\left(a+1\right)\left(2008^2a+1\right)}{\left(2008a+1\right)\left(2008^2a+1\right)}=\frac{2008^2a^2+\left(2008^2+1\right)a+1}{\left(2008a+1\right)\left(2008^2a+1\right)}\)
So sánh ở tử ta thấy \(2.2008
Đúng 0
Bình luận (0)
so sánh A =\(\dfrac{2009^{2008}+1}{2009^{2009}+1}\)
B = \(\dfrac{2009^{2009}+1}{2009^{2010}+1}\)
Nhanh nha đang cần gấp
Giải:
Ta có:
A=20092008+1/20092009+1
2009A=20092009+2009/20092009+1
2009A=20092009+1+2008/20092009+1
2009A=20092009+1/20092009+1 + 2008/20092009+1
2009A=1+2008/20092009+1
Tương tự:
B=20092009+1/20092010+1
2009B=1+2008/20092010+1
Vì 2008/20092009+1 > 2008/20092010+1 nên 2009A>2009B
⇒A>B
Đúng 0
Bình luận (0)
SO SÁNH CÁC SỐ SAU
A=2008^2009+2/2008^2009-1 vàB=2008^2009/2008^2009-3
ta có A = 2008^2009+2 / 2008^2009-1 = 2008^2009-1+3 / 2008^2009-1 = 1 + 3/2008^2009-1
lại có B = 2008^2009 / 2008^2009-3 = 2008^2009-3+3 / 2008^2009-3 = 1 + 3/2008^2009-3
vì 3/2008^2009-1 < 3/2008^2009-3 => 1 + 3/2008^2009-1 < 1 + 3/2008^2009-3
Hay A<B
Vậy A<B