Trong mp Oxy cho hình thang ABCD vuông tại A và D(2;2), CD=2AB. H là hình chiếu D trên AC, M là tđ HC. Bt pt DH:2x+y-5=0 BM: 4x+7y-61=0. Tìm tọa độ đỉnh
KR
Những câu hỏi liên quan
a) Cho hàm số yx^2-2x+2 có đồ thị (P) và đường thẳng (d) có pt yx+m. Tìm m để đường thẳng (P) cắt (d) tại hai điểm phân biệt A, E sao cho OA^2+OB^282b) Trong mp hệ tọa độ Oxy, cho hình thang vuông ABCD, widehat{A}widehat{D}90 có đỉnh D(2;2) và CD2AB. Gọi H là hình chiếu vuông góc của D lên đường chéo AC. Điểm Mleft(dfrac{22}{5};dfrac{14}{5}right) là trung điểm HC. Xác định tọa độ B, biết rằng B nằm trên đường thẳng Delta:x-2y+40
Đọc tiếp
a) Cho hàm số \(y=x^2-2x+2\) có đồ thị (P) và đường thẳng (d) có pt y=x+m. Tìm m để đường thẳng (P) cắt (d) tại hai điểm phân biệt A, E sao cho \(OA^2+OB^2=82\)
b) Trong mp hệ tọa độ Oxy, cho hình thang vuông ABCD, \(\widehat{A}=\widehat{D}=90\) có đỉnh D(2;2) và CD=2AB. Gọi H là hình chiếu vuông góc của D lên đường chéo AC. Điểm \(M\left(\dfrac{22}{5};\dfrac{14}{5}\right)\) là trung điểm HC. Xác định tọa độ B, biết rằng B nằm trên đường thẳng \(\Delta:x-2y+4=0\)
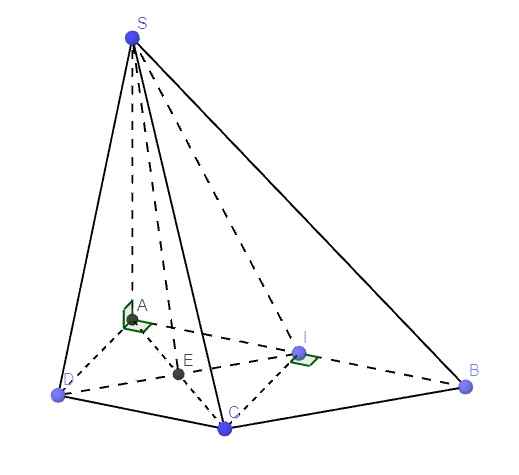
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB. SA vuông góc với (ABCD) a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
c.
Từ câu b ta có AICD là hình vuông \(\Rightarrow CI\perp AB\)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp CI\)
\(\Rightarrow CI\perp\left(SAB\right)\)
Lại có \(CI\in\left(SCI\right)\Rightarrow\left(SCI\right)\perp\left(SAB\right)\)
d.
I là trung điểm AB \(\Rightarrow CI\) là trung tuyến ứng với AB
Lại có \(CI=AD=a\) (AICD là hình vuông) \(\Rightarrow CI=\dfrac{1}{2}AB\)
\(\Rightarrow\Delta ACB\) vuông tại C
\(\Rightarrow BC\perp AC\) (1)
Mà \(SA\perp\left(ABCD\right)\Rightarrow SA\perp BC\) (2)
(1);(2) \(\Rightarrow BC\perp\left(SAC\right)\)
\(BC\in\left(SBC\right)\Rightarrow\left(SBC\right)\perp\left(SAC\right)\)
Đúng 2
Bình luận (0)
a.
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\left(gt\right)\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\)
Mà \(CD=\left(SCD\right)\cap\left(ABCD\right)\)
\(\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(tan\widehat{SDA}=\dfrac{SA}{AD}=\sqrt{3}\Rightarrow\widehat{SDA}=60^0\)
b.
Gọi E là giao điểm AC và DI
I là trung điểm AB \(\Rightarrow AI=\dfrac{1}{2}AB=a\Rightarrow AI=DC\)
\(\Rightarrow AICD\) là hình bình hành
Mà \(\widehat{A}=90^0\Rightarrow AICD\) là hình chữ nhật
\(AI=AD=a\) (hai cạnh kề bằng nhau) \(\Rightarrow AICD\) là hình vuông
\(\Rightarrow AC\perp DI\) tại E
Lại có \(SA\perp\left(ABCD\right)\Rightarrow SA\perp DI\Rightarrow DI\perp\left(SAE\right)\)
Mà \(DI=\left(SDI\right)\cap\left(ABCD\right)\Rightarrow\widehat{SEA}\) là góc giữa (SDI) và (ABCD)
\(AE=\dfrac{1}{2}AC=\dfrac{1}{2}\sqrt{AD^2+CD^2}=\dfrac{a\sqrt{2}}{2}\)
\(\Rightarrow tan\widehat{SEA}=\dfrac{SA}{AE}=\dfrac{\sqrt{6}}{2}\Rightarrow\widehat{SEA}\approx50^046'\)
Đúng 2
Bình luận (1)
Xem thêm câu trả lời
Cho hình chóp S.ABCD, đáy ABCD là hình thang vuông tại A và D. SA=a căn (3), AB=2a, AD=DC=a. Gọi I là trung điểm AB a. Tính góc giữa mp (SDC) và mp (ABCD) b. Tính góc giữa mp (SDI) và mp (ABCD) c. CM (SCI) vuông góc với (SAB) d. CM (SBC) vuông góc với (SAC)
Đề bài thiếu chi tiết định dạng điểm S nên không giải được (ví dụ phải thêm SA vuông góc mặt đáy hoặc gì đó tương tự)
Đúng 0
Bình luận (1)
trong mp OXY, cho hình thang cân ABCD có đáy lớn CD có diện tích bằng 45/2, CD: x-3y-3=0. Hai đường chéo AC và BD vuông góc với nhau tại I(2;3) viết phương trình BC biết C có hoành độ dương
* Gọi M, N lần lượt là trung điểm của AB và CD
Khi đó, MN vuông AB,CD; IM=MA=MB, IN=ND=NC
IN=d(I, CD)= => IC=ID=
Đường tròn (C) tâm I, bán kính R=IC có phương trình:
* Tọa độ C,D là nghiệm của hệ 2 phương trình: và x-3y-3=0
=> y=1 or y=-1 Vì C có hoành độ dương nên C(6,1) và D(0,-1)
* S=45/2 <=> 1/2. MN.(AB+CD)=45/2
<=> MN(2IM+2IN)=45
<=> MN^2=45/2 => MN=
=> IM=MN-IN=
Mà AB//CD => =>
vói => B(3,5) và C(6,1)
Vậy BC: 4x+3y-27=0
Đúng 0
Bình luận (1)
Cho hình thang vuông ABCD vuông ở A và D, AD = 2a. Trên đường thẳng vuông góc tại D với (ABCD) lấy điểm S với S D = a 2
- Tính khỏang cách giữa đường thẳng CD và mp(SAB).
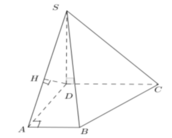
+) Vì ABCD là hình thang nên: CD // AB ⇒ CD// mp(SAB).
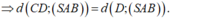
- Kẻ DH ⊥ SA.
+) Ta có:
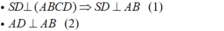
- Từ (1) và (2) suy ra:
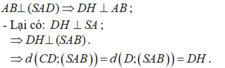
- Trong tam giác vuông SAD ta có:
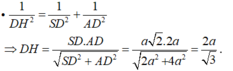
Đúng 0
Bình luận (0)
trong mặt phẳng với hệ tọa độ Oxy, cho hình thang vuông ABCD ( vuông tại A và B ) . Gọi M(-3,-3) N lần lược là trung điểm của AD và AB . Xác định tọa độ các đỉnh của hình thang vuông ABCD , biết phương trình các đường thẳng BD: 7x+3y+2=0, CN: x-3y=0, CN: x-y=0và đường thẳng AB đi qua điểm e (-3;1)
Đường CN có pt là x-3y=0 hay x-y=0 vậy bạn?
Đúng 0
Bình luận (0)
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và D. Biết rằng SAperp mpleft(ABCDright) , gọi M là hình chiếu vuông góc của A lên cạnh SD . Giả sử rằng AB2.AD2.DC2.a , độ dài cạnh SA2a Tính khoảng cách từ điểm M đến mpleft(SBCright)P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em với ạEm cám ơn nhiều ạ!
Đọc tiếp
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại \(A\) và \(D\). Biết rằng \(SA\perp mp\left(ABCD\right)\) , gọi M là hình chiếu vuông góc của \(A\) lên cạnh \(SD\) .
Giả sử rằng \(AB=2.AD=2.DC=2.a\) , độ dài cạnh \(SA=2a\)
Tính khoảng cách từ điểm \(M\) đến \(mp\left(SBC\right)\)
P/s: Em xin phép nhờ quý thầy cô giáo và các bạn yêu toán gợi ý giúp đỡ em với ạ
Em cám ơn nhiều ạ!
Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A và B, Kẻ SA vuông góc với mpleft(ABCDright). Biết rằng ABBCa, AD2a góc giữa SB và mpleft(ABCDright) bằng 45^0a) Chứng minh rằng BC vuông góc với SB, và mpleft(SCDright)perp mpleft(SACright)b) Gọi mpleft(alpharight) là mặt phẳng đi qua A và vuông góc với SC. Xác định thiết diện của hình chóp S.ABCD và mpleft(alpharight). Tính diện tích của thiết diện đó theo a.P/s: Em xin nhờ quý thầy cô giáo và các bạn yêu toán...
Đọc tiếp
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình thang vuông tại A và B, Kẻ \(SA\) vuông góc với \(mp\left(ABCD\right)\). Biết rằng \(AB=BC=a\), \(AD=2a\) góc giữa \(SB\) và \(mp\left(ABCD\right)\) bằng \(45^0\)
a) Chứng minh rằng BC vuông góc với SB, và \(mp\left(SCD\right)\perp mp\left(SAC\right)\)
b) Gọi \(mp\left(\alpha\right)\) là mặt phẳng đi qua A và vuông góc với SC. Xác định thiết diện của hình chóp \(S.ABCD\) và \(mp\left(\alpha\right)\). Tính diện tích của thiết diện đó theo \(a\).
P/s: Em xin nhờ quý thầy cô giáo và các bạn yêu toán trên toàn quốc giúp em ý b với ạ
Em cám ơn nhiều lắm ạ!
Cho hình chóp S.ABCD có SA vuông góc với mp đáy (ABCD) và ABCD là hình thang vuông tại A, đáy lớn AB, AB=2a, AD=CD=a. Gọi H là hình chiếu vuông góc của A lên SC và E là trung điểm của AB
a, CMR: (SCD) ⊥(SAD) và AH ⊥(SBC)
b, Biết góc giữa 2 mp (SCD) và (ABCD) bằng 300. Tính góc giữa 2 mp (SAD) và (SCE)?
\(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp CD\\CD\perp AD\end{matrix}\right.\) \(\Rightarrow CD\perp\left(SAD\right)\Rightarrow\left(SCD\right)\perp\left(SAD\right)\)
\(AC=\sqrt{AD^2+CD^2}=a\sqrt{2}\)
\(BC=\sqrt{BE^2+CE^2}=a\sqrt{2}\)
\(\Rightarrow AC^2+BC^2=AB^2\Rightarrow AC\perp BC\)
\(\Rightarrow BC\perp\left(SAC\right)\Rightarrow BC\perp AH\Rightarrow AH\perp\left(SBC\right)\)
b.
\(CD\perp\left(SAD\right)\Rightarrow\widehat{SDA}\) là góc giữa (SCD) và (ABCD)
\(\Rightarrow\widehat{SDA}=30^0\Rightarrow SA=AD.tan30^0=\dfrac{a\sqrt{3}}{3}\)
Ta có: \(\left\{{}\begin{matrix}SA\perp\left(ABCD\right)\Rightarrow SA\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(SAB\right)\)
Qua S kẻ đường thẳng d song song AD
Do \(AD||CE\) \(\Rightarrow\) d là giao tuyến (SAD) và (SCE)
Mà \(d\perp\left(SAB\right)\Rightarrow\widehat{ASE}\) là góc giữa (SAD) và (SCE)
\(AE=\dfrac{AB}{2}=a\)
\(tan\widehat{ASE}=\dfrac{AE}{SA}=\sqrt{3}\Rightarrow\widehat{ASE}=60^0\)
Đúng 2
Bình luận (2)