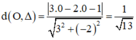Tìm khoảng cách từ điểm O(0;0) đến đg thẳng denta : x /6+y/8=1
A 4,8
B 1/10
C 1/14
D 48/căn14
tìm khoảng cách từ điểm -1 đến điểm 7 a <0
tìm khoảng cách từ điểm -2 đến điểm -8
Khoảng cách từ -1 đến 7 là
7 - ( -1) = 8
Khoảng cách từ -2 đến -8 là
-8 - -2 = -6
k nhé  Chu Quang Dũng
Chu Quang Dũng
Khoảng các từ -1 đến 7 lấy 7 - (-1 ) = 8
Khoảng cách từ -2 đến -8 là:
(-8) - (-2) = 6.
Đáp số: 8 ; 6.
8;6 nha bạn
Chúc các bạn học giỏi
Tết vui vẻ nha
tìm khoảng cách từ điểm -1 đến điểm 7 a <0
tìm khoảng cách từ điểm -2 đến điểm -8
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15
Quan sát trục số:
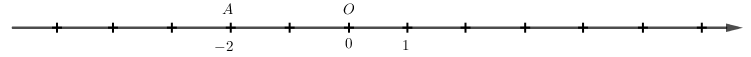
a) Tính khoảng cách từ điểm O đến điểm A.
b) Tìm trên trục số những điểm cách điểm O một khoảng là 5 đơn vị.
a) Khoảng cách từ điểm O đến điểm A: 2 đơn vị.
b) Những điểm cách O một khoảng là 5 đơn vị là: điểm 5 và -5.
a) Khoảng cách từ điểm O đến điểm A = |0-(-2)| = 2
b) Các điểm cách O một khoảng 5 đơn vị là: -7 và 3
a) Khoảng cách từ điểm O đến điểm A: 2 đơn vị.
b) Những điểm cách O một khoảng là 5 đơn vị là: điểm 5 và -5.
tính khoảng cách điiểm gốc o đến mỗi điểm M,Q,R theo mẫu M -6 N -2 0 1 P Q R 7
mẫu khoảng cách từ 0 đến điểm N là 2 đơn vị
khoảng cách từ 0 đến P là 1 đơn vị
b) tính khoảng cách từ điểm gốc 0đến các điểm biểu diễn các số:-8;6;-50;15
Cho đường thẳng d : y = (m + 1) x – m + 2 (m là tham số)
a. Tìm điểm I là điểm cố định mà d luôn đi qua với mọi m.
b. Hỏi khoảng cách từ O (0; 0) đến d là bao nhiêu ?
Lời giải:
a. Gọi $I(x_0,y_0)$ là điểm cố định mà $(d)$ luôn đi qua. Ta có:
$y_0=(m+1)x_0-m+2, \forall m$
$m(x_0-1)+(x_0+2-y_0)=0, \forall m$
\(\Leftrightarrow \left\{\begin{matrix} x_0-1=0\\ x_0+2-y_0=0\end{matrix}\right.\Leftrightarrow \Rightarrow \left\{\begin{matrix} x_0=1\\ y_0=3\end{matrix}\right.\)
Vậy $I(1,3)$ là điểm cố định mà $d$ luôn đi qua với mọi $m$
b.
$A(0,a)$ là giao của $(d)$ với trục $Oy$
$B(b,0)$ là giao của $(d)$ với trục $Ox$
Nếu $m=-1$ thì $y=3$
Khi đó, khoảng cách từ $O$ đến $(d)$ là $3$
Nếu $m\neq -1$ thì:
$a=(m+1).0-m+2=-m+2$
$b=\frac{m-2}{m+1}$
Theo hệ thức lượng trong tam giác vuông thì khoảng cách từ $O$ đến $(d)$ là $h$ thì:
$\frac{1}{h^2}=\frac{1}{a^2}+\frac{1}{b^2}$
$=\frac{1}{(m-2)^2}+\frac{(m+1)^2}{(m-2)^2}=\frac{m^2+2m+2}{(m-2)^2}$
$\Rightarrow h=\frac{|m-2|}{\sqrt{m^2+2m+2}}$
Quan sát Hình 84 và cho biết:
a) Khoảng cách từ điểm O đến đường thẳng a;
b) Khoảng cách từ điểm O đến đường thẳng b;
c) Khoảng cách từ điểm O đến đường thẳng c.
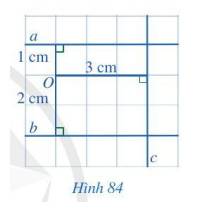
a) Khoảng cách từ điểm O đến đường thẳng a bằng 1 cm;
b) Khoảng cách từ điểm O đến đường thẳng b bằng 2 cm;
c) Khoảng cách từ điểm O đến đường thẳng c bằng 3 cm.
Trong không gian Oxyz, cho các điểm M(0;0;0), N(0;n;0), P(0;0;p) không trùng với gốc tọa độ và thỏa mãn m 2 + n 2 + p 2 = 3 . Tìm giá trị lớn nhất của khoảng cách từ điểm O đến mặt phẳng (MNP)
A. 1 3
B. 3
C. 1 3
D. 1 27
Trong không gian Oxyz, cho các điểm M ( 0 ; 0 ; 0 ) , N ( 0 ; n ; 0 ) , P ( 0 ; 0 ; p ) không trùng với gốc tọa độ và thỏa mãn m 2 + n 2 + p 2 = 3 . Tìm giá trị lớn nhất của khoảng cách từ điểm O đến mặt phẳng (MNP)
A . 1 3 .
B . 3 .
C . 1 3 .
D . 1 27 .
Tính khoảng cách từ các điểm M(-2; 1) và O(0; 0) đến đường thẳng Δ có phương trình 3x – 2y - 1 = 0.
Khoảng cách từ điểm M (-2; 1) đến đường thẳng Δ là:
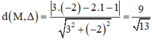
Khoảng cách từ điểm O (0; 0) đến đường thẳng Δ là: