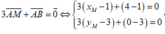\(R=d\left(I;\Delta\right)=\dfrac{\left|3.3-4.\left(-1\right)+2\right|}{\sqrt{3^3+\left(-4\right)}^2}=3\)

Phương trình đường tròn có tâm \(I\left(3;-1\right)\) và \(R=3\)

\(\Rightarrow\left(x-3\right)^2+\left(y+1\right)^2=9\)

Tọa độ điểm I của đoạn thẳng MN là:

x I = x M + ​ x N 2 = 0 + ​ ( − 3 ) 2 = − 3 2 y I = y M + ​ y N 2 = 4 + ​ 2 2 = 3 ⇒ I − 3 2 ;    3

Đáp án C

Đáp án C đúng

\(\left\{{}\begin{matrix}x_{M'}=2x_M=2.3=6\\y_{M'}=2y_M=2.\left(-2\right)=-4\end{matrix}\right.\)

\(\Rightarrow M'\left(6;-4\right)\)

Đặt AB=a

=>\(MB=MN=a\sqrt{10};BN=2a\sqrt{5}\)

=>ΔBMN vuông cân tại M và J là trung điểm của BN

=>MJ vuông góc NJ

=>NJ: x-5=0

Tọa độ J là:

x-5=0 và 2y-7=0

=>x=5 và y=7/2

Vì J là trung điểm của BN nên B(5;1)

Gọi C(x,y), x>3

BC=2NC=2 căn 5

Ta có HPT:

(x-5)^2+(y-1)^2=20 và (x-5)^2+(y-6)^2=5

=>x=7 và y=5(nhận) hoặc x=3 và y=5(loại)

=>C(7;5)

Theo công thức trung điểm:

\(\left\{{}\begin{matrix}x_M=2x_B-x_A=5\\y_M=2y_B-y_A=6\end{matrix}\right.\) \(\Rightarrow M\left(5;6\right)\)

Để B là trung điểm của đoạn thẳng AM, ta cần tìm tọa độ của điểm M.

Theo định nghĩa, trung điểm của một đoạn thẳng là điểm nằm ở giữa hai đầu mút của đoạn đó. Ta áp dụng công thức trung điểm để tìm tọa độ của M.

Công thức trung điểm: M(xM, yM) là trung điểm của đoạn AB <=> (xM, yM) = ((xA + xB)/2, (yA + yB)/2).

Ứng với A(1; -2) và B(3; 2): xM = (1 + 3)/2 = 2, yM = (-2 + 2)/2 = 0.

Vậy tọa độ của điểm M là M(2; 0).

Đáp án đúng là: B. M(2; 0).

\(\left\{{}\begin{matrix}\overrightarrow{AM}=\left(x-1;y-3\right)\\\overrightarrow{BM}=\left(x-4;y-2\right)\end{matrix}\right.\)

Tam giác ABM vuông cân tại M khi:

\(\left\{{}\begin{matrix}\overrightarrow{AM}.\overrightarrow{BM}=0\\AM^2=BM^2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}\left(x-1\right)\left(x-4\right)+\left(y-3\right)\left(y-2\right)=0\\\left(x-1\right)^2+\left(y-3\right)^2=\left(x-4\right)^2+\left(y-2\right)^2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-5x+y^2-5y+10=0\\3x-y=5\end{matrix}\right.\)

Thế \(y=3x-5\) lên pt trên:

\(x^2-5x+\left(3x-5\right)^2-5\left(3x-5\right)+10=0\)

\(\Leftrightarrow x^2-5x+6=0\Rightarrow\left[{}\begin{matrix}x=2\Rightarrow y=1\\x=3\Rightarrow y=4\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}M\left(2;1\right)\\M\left(3;4\right)\end{matrix}\right.\)

Gọi d' là đường thẳng qua M và vuông góc d \(\Rightarrow d'\) nhận (3;1) là 1 vtpt

Phương trình d':

\(3\left(x-1\right)+1\left(y+8\right)=0\Leftrightarrow3x+y+5=0\)

Gọi A là giao điểm d và d' \(\Rightarrow\) tọa độ A là nghiệm:

\(\left\{{}\begin{matrix}3x+y+5=0\\x-3y+5=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=-2\\y=1\end{matrix}\right.\) \(\Rightarrow A\left(-2;1\right)\)

M' đối xứng M qua d khi và chỉ khi A và trung điểm MM'

\(\Rightarrow\left\{{}\begin{matrix}x_{M'}=2x_A-x_M=-5\\y_{M'}=2y_A-y_M=10\end{matrix}\right.\) \(\Rightarrow M\left(-5;10\right)\)

Chọn B

Ta có: