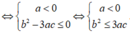Ai chỉ giúp mình câu này với!!!
Cho hàm số y= ax3 + bx2 + cx +d. Biết M(0;2), N(2;-2) là các điểm cực trị của đồ thị hàm số. Inhs giá trị của hàm số tại x=-2.
HB
Những câu hỏi liên quan
Biết phương trình
a
x
3
+
b
x
2
+
c
x
+
d
0
a
≠
0
có đúng hai nghiệm thực. Hỏi đồ thị hàm số
y
a
x
3
+
b
x
2
+
c...
Đọc tiếp
Biết phương trình a x 3 + b x 2 + c x + d = 0 a ≠ 0 có đúng hai nghiệm thực. Hỏi đồ thị hàm số y = a x 3 + b x 2 + c x + d có bao nhiêu điểm cực trị?
A. 4
B. 5
C. 6
D. 3
Cho hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
có đồ thị trong hình bên. Hỏi phương trình y
a
x
3
+
b
x
2
+
c
x
+
d
+
1
0
có bao nhiêu nghiệm? A. Phương trình không có nghiệ...
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d có đồ thị trong hình bên. Hỏi phương trình y = a x 3 + b x 2 + c x + d + 1 = 0 có bao nhiêu nghiệm?
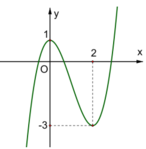
A. Phương trình không có nghiệm
B. Phương trình có đúng một nghiệm.
C. Phương trình có đúng hai nghiệm.
D. Phương trình có đúng ba nghiệm
Cho hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
có đồ thị như hình bên. Hỏi phương trình
a
x
3
+
b...
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d có đồ thị như hình bên. Hỏi phương trình a x 3 + b x 2 + c x + d = 0 có bao nhiêu nghiệm?
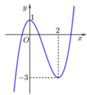
A. Phương trình không có nghiệm
B. Phương trình có đúng một nghiệm
C. Phương trình có đúng hai nghiệm
D. Phương trình có đúng ba nghiệm
Biết phương trình
a
x
3
+
b
x
2
+
c
x
+
d
0
a
≠
0
. Có đúng hai nghiệm thực. Hỏi đồ thị hàm số
y
a
x
3
+
b
x...
Đọc tiếp
Biết phương trình a x 3 + b x 2 + c x + d = 0 a ≠ 0 . Có đúng hai nghiệm thực. Hỏi đồ thị hàm số y = a x 3 + b x 2 + c x + d có bao nhiêu điểm cực trị?
A. 4
B. 3
C. 5
D. 2
Hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
,
a
≠
0
luôn đồng biến trên
ℝ
khi và chỉ khi A.
a
0
b...
Đọc tiếp
Hàm số y = a x 3 + b x 2 + c x + d , a ≠ 0 luôn đồng biến trên ℝ khi và chỉ khi
A. a > 0 b 2 − a c < 0
B. a > 0 b 2 − 3 a c < 0
C. a > 0 b 2 − 3 a c > 0
D. a > 0 b 2 − 3 a c ≤ 0
Đáp án D
Ta có: Hàm số luôn đồng biến trên
ℝ ⇔ y ' = 3 a x 2 + 2 b x + c ≥ 0 ∀ x ∈ ℝ ⇔ a > 0 Δ y ' = b 2 − 3 a c ≤ 0
Đúng 0
Bình luận (0)
Cho hàm số
y
f
x
a
x
3
+
b
x
2
+
c
x
+
d
với
a
≠
0.
Biết đồ thị hàm số có hai điểm cực trị là
A
1
;
−
1
,
B...
Đọc tiếp
Cho hàm số y = f x = a x 3 + b x 2 + c x + d với a ≠ 0. Biết đồ thị hàm số có hai điểm cực trị là A 1 ; − 1 , B − 1 ; 3 . Tính f 4 .
A. f 4 = − 17
B. f 4 = 53
C. f 4 = − 53
D. f 4 = 17
Đáp án B
Ta có
f ' x = 3 a x 2 + 2 b x + c ⇒ f ' 1 = 3 a + 2 b + c = 0 f ' − 1 = 3 a − 2 b + c = 0
Mặt khác
f 1 = a + b + c + d = − 1 f − 1 = − a + b − c + d = 3 ⇒ a = 1 ; b = 0 c = − 3 ; d = 1 ⇒ f x = x 3 − 3 x + 1 ⇒ f 4 = 53
Đúng 0
Bình luận (0)
Cho đồ thị hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
có điểm cực đại là A(-2;2), điểm cực tiểu là B(0;-2). Tìm tất cả các giá trị của m để phương trình
a
x
3
+
b
x
2
+
c
x
+
d
m
có 3 nghiệm phân biệt. A.
m
2
B.
m...
Đọc tiếp
Cho đồ thị hàm số y = a x 3 + b x 2 + c x + d có điểm cực đại là A(-2;2), điểm cực tiểu là B(0;-2). Tìm tất cả các giá trị của m để phương trình a x 3 + b x 2 + c x + d = m có 3 nghiệm phân biệt.
A. m > 2
B. m < - 2
C. - 2 < m < 2
D. m = 2 m = - 2
Đáp án C
Phương trình có ba nghiệm phân biệt nếu y c t < m < y c d ⇔ - 2 < m < 2
Đúng 0
Bình luận (0)
Cho hàm số
y
a
x
3
+
b
x
2
+
c
x
+
d
.
Hàm số luôn đồng biến trên
ℝ
khi và chỉ khi A.
a
b
0
,...
Đọc tiếp
Cho hàm số y = a x 3 + b x 2 + c x + d . Hàm số luôn đồng biến trên ℝ khi và chỉ khi
A. a = b = 0 , c > 0 a > 0 , b 2 − 3 a c ≥ 0
B. a > 0 , b 2 − 3 a c ≤ 0
C. a = b = 0 , c > 0 a > 0 , b 2 − 3 a c ≤ 0
D. a = b = 0 , c > 0 a > 0 , b 2 − 4 a c ≤ 0
Cho hàm số y ax3+ bx2+ cx+ d có đồ thị như hình vẽ bên. Đồ thị hàm số y |ax3+ bx2+ cx+ d + 1| có bao nhiêu điểm cực trị? A. 2 B. 3 C. 4 D. 5
Đọc tiếp
Cho hàm số y = ax3+ bx2+ cx+ d có đồ thị như hình vẽ bên. Đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| có bao nhiêu điểm cực trị?
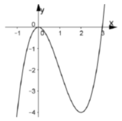
A. 2
B. 3
C. 4
D. 5
Ta có thể vẽ đồ thị hàm số y = |ax3+ bx2+ cx+ d + 1| theo ba bước sau:
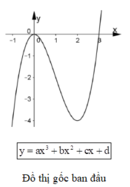
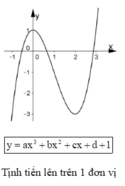
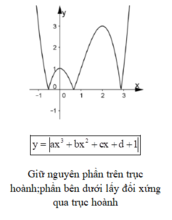
Dựa vào đồ thị ta thấy hàm số có 4 cực trị
Chọn C.
Đúng 0
Bình luận (0)
Cho hàm số
f
x
a
x
3
+
b
x
2
+
c
x
+
d
với
a
,
b
,...
Đọc tiếp
Cho hàm số f x = a x 3 + b x 2 + c x + d với a , b , c , d là các hệ số thực và a ≠ 0 . Hàm số f x nghịch biến trên ℝ khi và chỉ khi:
A. a < 0 b 2 ≤ 3 a c
B. a < 0 b 2 < 3 a c
C. a > 0 b 2 ≥ 3 a c
D. a > 0 b 2 < 3 a c
Chọn A
Ta có: f ' x = 3 a x 2 + 2 b x + c
có ∆ ' f ' x = b 2 - 3 a c .
Hàm số f x nghịch biến trên ℝ khi và chỉ khi
3 a < 0 ∆ ' f ' x ≤ 0
Đúng 0
Bình luận (0)