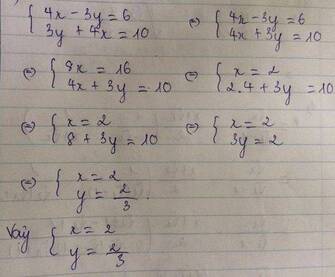4x = 3y; y/3 = z/5 và 3x - z = 21
DT
Những câu hỏi liên quan
Giải các hệ phương trình sau:
c.{3x + y = 10
4x - 3y = 9
d.{4x + 3y = 22
5x + 3y = 26
e.{4x - 3y = 5
5x + 3y = 13
\(c,\left\{{}\begin{matrix}3x+y=10\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+3y=30\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=39\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\\ d,\left\{{}\begin{matrix}4x+3y=22\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=2\end{matrix}\right.\\ e,\left\{{}\begin{matrix}4x-3y=5\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=18\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Đúng 4
Bình luận (0)
c: \(\left\{{}\begin{matrix}3x+y=10\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}12x+4y=40\\12x-9y=27\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}13y=13\\3x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=1\\x=3\end{matrix}\right.\)
d: \(\left\{{}\begin{matrix}4x+3y=22\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-x=-4\\4x+3y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=\dfrac{22-4x}{3}=\dfrac{22-4\cdot4}{3}=2\end{matrix}\right.\)
Đúng 1
Bình luận (0)
c. \(\left\{{}\begin{matrix}3x+y=10\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+3y=30\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=39\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
d. \(\left\{{}\begin{matrix}4x+3y=22\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\4x+3y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=2\end{matrix}\right.\)
e. \(\left\{{}\begin{matrix}4x-3y=5\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=18\\4x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Giải các hệ phương trình sau:
a.|3x - y = 5
|4x + 2y = 10
b.|5x + 2y = 9
|x + 5y = 11
c.|3x + y = 10
|4x - 3y = 9
d.|4x + 3y = 22
|5x + 3y = 26
e.|4x - 3y = 5
|5x + 3y = 13
Giải các hệ phương trình sau:
a.{3x - y = 5
4x + 2y = 10
b.{5x + 2y = 9
x + 5y = 11
c.{3x + y = 10
4x - 3y = 9
d.{4x + 3y = 22
5x + 3y = 26
e.{4x - 3y = 5
5x + 3y = 13
\(a,\left\{{}\begin{matrix}3x-y=5\\4x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x-y=5\\2x+y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\\ b,\left\{{}\begin{matrix}5x+2y=9\\x+5y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+2y=9\\5x+25y=55\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+2y=9\\23y=46\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\)
\(c,\left\{{}\begin{matrix}3x+y=10\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+3y=30\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=39\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\\ d,\left\{{}\begin{matrix}4x+3y=22\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=2\end{matrix}\right.\)
\(e,\left\{{}\begin{matrix}4x-3y=5\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=18\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Đúng 3
Bình luận (0)
a. \(\left\{{}\begin{matrix}3x-y=5\\4x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}6x-2y=10\\4x+2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x=20\\6x-2y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
b. \(\left\{{}\begin{matrix}5x+2y=9\\x+5y=11\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}5x+2y=9\\5x+25y=55\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}23y=46\\5x+2y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=1\end{matrix}\right.\)
c. \(\left\{{}\begin{matrix}3x+y=10\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x+3y=30\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}13x=39\\4x-3y=9\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=1\end{matrix}\right.\)
d. \(\left\{{}\begin{matrix}4x+3y=22\\5x+3y=26\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\4x+3y=22\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=4\\y=2\end{matrix}\right.\)
e. \(\left\{{}\begin{matrix}4x-3y=5\\5x+3y=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9x=18\\4x-3y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=1\end{matrix}\right.\)
Đúng 1
Bình luận (0)
a) \(\begin{cases} 3x -y=5\\ 4x +2y=10 \end{cases} \)
\(\begin{cases} 12x - 4y= 20\\ 12x +6y= 30 \end{cases} \)
\(\begin{cases} -10y=-10\\ 3x-y=5 \end{cases} \)
\(\begin{cases} y=1\\ 3x-1=5 \end{cases} \)
\(\begin{cases} y=1\\ 3x=6 \end{cases} \)
\(\begin{cases} y=1\\ x=2 \end{cases} \)
Hpt có nghiệm duy nhất: {1;2}
b)\(\begin{cases} 5x +2y=9\\ x+5y=11 \end{cases} \)
\(\begin{cases} 5x+2y=9\\ 5x+25y=55 \end{cases} \)
\(\begin{cases} -23y=-46\\ x+5y=11 \end{cases} \)
\(\begin{cases} y=2\\ x+ 5*2=11 \end{cases} \)
\(\begin{cases} y=2\\ x+10=11 \end{cases} \)
Hpt có nghiệm duy nhất:{1;2}
c)\(\begin{cases} 3x+y=10\\ 4x-3y=9 \end{cases} \)
\(\begin{cases} 12x+4y=40\\ 12x-9y=27 \end{cases} \)
\(\begin{cases} 13y=13\\ 3x+y=10 \end{cases} \)
\(\begin{cases} y=1\\ 3x+1=10 \end{cases} \)
\(\begin{cases} y=1\\ 3x=9 \end{cases} \)
hpt có nghiệm duy nhất:{1;3}
d)\(\begin{cases} 4x+3y=22\\ 5x+3y=26 \end{cases} \)
\(\begin{cases} 20x+15y=110\\ 20x+12y=104 \end{cases} \)
\(\begin{cases} 3y=6\\ 4x+3y=22 \end{cases} \)
\(\begin{cases} y=2\\ 4x+3*2=22 \end{cases} \)
\(\begin{cases} y=2\\ 4x+6=22 \end{cases} \)
hệ phương trình có nghiệm duy nhất:{2;4}
e)\(\begin{cases} 4x-3y=5\\ 5x+3y=13 \end{cases} \)
\(\begin{cases} 20x-15y=25\\ 20x+12y=52 \end{cases} \)
\(\begin{cases} -27y=-27\\ 4x-3y=5 \end{cases} \)
\(\begin{cases} y=1\\ 4x-3*1=5 \end{cases} \)
\(\begin{cases} y=1\\ 4x-3=5 \end{cases} \)
Hệ phương trình có nghiệm duy nhất là:{1;2}
Đúng 1
Bình luận (0)
Giải các hệ phương trình sau:
a.|3x - y = 5
|4x + 2y = 10
b.|5x + 2y = 9
|x + 5y = 11
c.|3x + y = 10
|4x - 3y = 9
d.|4x + 3y = 22
|5x + 3y = 26
e.|4x - 3y = 5
|5x
Câu: Đẳng thức nào sau đây là đúng. *
4x^3y^2 – 8x^2y^3 = 4x^2.y(xy – 2y^2)
4x^3y^2 – 8x^2y^3 = 4x^2y^2(x – 2y)
4x^3y^2 – 8x^2y^3 = x^2y^2(x – 2y)
4x^3y^2 – 8x^2y^3 = 4x^2y^2(x – y)
ta có 4 x 3 y 2 – 8 x 2 y 3 = 4 x 2 y 2 . x – 4 x 2 y 2 . 2 y = 4 x 2 y 2 ( x – 2 y )
Vậy 4x3y2 – 8x2y3 = 4x2y2(x – 2y)
Đáp án cần chọn là: C
bấm đúng cho mik đi
Đúng 3
Bình luận (0)
giải hệ phương trình 4x-3y=6 và 3y+4x=10
a)-6x^3y^2:2xy^2. b)-1/4x^4y^3:1/2x^3y^2. c) 8x^4y^5:4x^3y^4
a: \(=\left(-\dfrac{6}{2}\right)\cdot\dfrac{x^3}{x}\cdot\dfrac{y^2}{y^2}=-3x^2\)
b: \(=\left(-\dfrac{1}{4}:\dfrac{1}{2}\right)\cdot\dfrac{x^4}{x^3}\cdot\dfrac{y^3}{y^2}=-\dfrac{1}{2}xy\)
c: \(=\dfrac{8}{4}\cdot\dfrac{x^4}{x^3}\cdot\dfrac{y^5}{y^4}=2xy\)
Đúng 0
Bình luận (0)
\(a,-6x^3y^2:2xy^2=-3x^2\)
\(b,-\dfrac{1}{4}x^4y^3:\dfrac{1}{2}x^3y^2=-\dfrac{1}{2}xy\)
\(c,8x^4y^5:4x^3y^4=2xy\)
#Urushi
Đúng 0
Bình luận (0)
Tìm x, y biết: 4x - 3/3 = 3y + 1/7 = 4x + 3y -2/ 5y
\(\frac{4x-3}{3}=\frac{3y+1}{7}=\frac{4x+3y-2}{5y}\)
\(=\frac{4x-3+3y+1-\left(4x+3y-2\right)}{3+7-5y}\)
\(=\frac{4x-3+3y+1-4x-3y+2}{10-5y}\)
\(=\frac{\left(4x-4x\right)+3y-3y-3+1+2}{10-5y}=0\)
\(\Rightarrow\hept{\begin{cases}4x-3=0\Leftrightarrow x=\frac{3}{4}\\3y+1=0\Leftrightarrow y=-\frac{1}{3}\end{cases}}\)
Vậy \(x=\frac{3}{4};y=-\frac{1}{3}\).
Đúng 0
Bình luận (0)
Câu trả lời đúng là :
x = 3/4
y = -1/3
Đáp số : ...
Đúng 0
Bình luận (0)
Tìm tập xác định của biểu thức, rút gọn biểu thức, rồi tính giá trị của biểu thức với x = \(\dfrac{1}{3}\) , y = -2:
[\(\dfrac{2x}{2x-3y}\) - \(\dfrac{9y^2\left(3y+4x\right)}{8x^3-37y^3}\) - \(\dfrac{24xy}{4x^2+6xy+9y^2}\)][2x + \(\dfrac{3y\left(3y+4x\right)}{2x-3y}\)]
Đặt bthuc = A nhé
ĐKXĐ : \(2x\ne3y\)
\(A=\left[\dfrac{2x\left(4x^2+6xy+9y^2\right)}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}-\dfrac{27y^3+36xy^2}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}-\dfrac{24xy\left(2x-3y\right)}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}\right]\left[\dfrac{2x\left(2x-3y\right)}{\left(2x-3y\right)}+\dfrac{9y^2+12xy}{\left(2x-3y\right)}\right]\)\(=\left[\dfrac{8x^3+12x^2y+18xy^2-27y^3-36xy^2-48x^2y+72xy^2}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}\right]\left[\dfrac{4x^2-6xy+9y^2+12xy}{\left(2x-3y\right)}\right]\)
\(=\dfrac{8x^3-36x^2y+36xy^2-27y^3}{\left(2x-3y\right)\left(4x^2+6xy+9y^2\right)}\cdot\dfrac{4x^2+6xy+9y^2}{2x-3y}\)
\(=\dfrac{\left(2x-3y\right)^3}{\left(2x-3y\right)^2}=2x-3y\)
Với x = 1/3 ; y = -2 (tmđk) thay vào A ta được : A = 2.1/3 - 3.(-2) = 20/3
Đúng 0
Bình luận (0)
Tính khoảng cách giữa hai đường thẳng \({d_1}:4x - 3y + 2 = 0\) và \({d_2}:4x - 3y + 12 = 0\).
Ta thấy hai đường thẳng này song song, nên khoảng cách giữa chúng là khoảng cách từ một điểm bất kì từ đường thẳng này tới đường thẳng kia
Chọn điểm \(A\left( {0;4} \right) \in {d_2}\), suy ra \(d\left( {{d_1},{d_2}} \right) = d\left( {A,{d_1}} \right) = \frac{{\left| {4.0 - 3.4 + 2} \right|}}{{\sqrt {{4^2} + {3^2}} }} = 2\)
Vậy khoảng cách giữa hai đường thẳng \({d_1}:4x - 3y + 2 = 0\) và \({d_2}:4x - 3y + 12 = 0\) là 2
Đúng 0
Bình luận (0)