Cho tam giác ABC có A 900; AB < AC ; phân giác BE, E thuộc AC . Kẻ
EH⊥BC(H thuộc BC)
a) Chứng minh AB = BH .
b) Gọi I là giao điểm của AH và BE, chứng minh AI = IH và BI⊥AH
KW
Những câu hỏi liên quan
Tam giác vuông ABC ( ∠ A = 90 0 ) có AB = 6cm, AC = 8cm và tam giác vuông A’B’C’ ( ∠ A ' = 90 0 ) có A’B’ = 9cm, B’C’ = 15cm. Hỏi rằng hai tam giác vuông ABC và A’B’C’ có đồng dạng với nhau không? Vì sao?
* Trong tam giác vuông A’B’C’ có ∠ A ' = 90 0
Áp dụng định lí Pi-ta-go, ta có: A ' B ' 2 + A ' C ' 2 = B ' C ' 2
Suy ra: A ' C ' 2 = B ' C ' 2 - A ' B ' 2 = 15 2 - 9 2 = 144
Suy ra: A’C’ = 12 (cm)
* Trong tam giác vuông ABC có ∠ A = 90 0
Áp dụng định lí Pi-ta-go, ta có: B C 2 = A B 2 + A C 2 = 6 2 + 8 2 =100
Suy ra: BC = 10 (cm)
Ta có: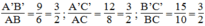 
Suy ra: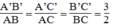 
Vậy △ A’B’C’ đồng dạng ΔABC (c.c.c)
Đúng 0
Bình luận (0)
Cho tam giác ABC và tam giác DEF có:
B
^
E
^
90
0
,
A
C
D
F
,
A
^
F
^
. Phát biểu nào sau đây đúng? A.
Δ
A
B
C
Δ
F
E
D
B.
Δ
A
B
C
Δ
F
D...
Đọc tiếp
Cho tam giác ABC và tam giác DEF có: B ^ = E ^ = 90 0 , A C = D F , A ^ = F ^ . Phát biểu nào sau đây đúng?
A. Δ A B C = Δ F E D
B. Δ A B C = Δ F D E
C. Δ B A C = Δ F E D
D. Δ A B C = Δ D E F
Cho tam giác ABC và tam giác KHI có:
A
^
K
^
90
0
,
A
B
K
H
,
B
C
H
I
. Phát biểu nào sau đây đúng? A.
Δ
A
B
C
Δ
K
H
I
B.
Δ
A
B
C
Δ
H
K
I
C.
Δ...
Đọc tiếp
Cho tam giác ABC và tam giác KHI có: A ^ = K ^ = 90 0 , A B = K H , B C = H I . Phát biểu nào sau đây đúng?
A. Δ A B C = Δ K H I
B. Δ A B C = Δ H K I
C. Δ A B C = Δ K I H
D. Δ A C B = Δ K H I
Xét tam giác ABC và tam giác KHI có:
A ^ = K ^ = 90 0 , A B = K H , B C = H I
Suy ra: Δ A B C = Δ K H I (cạnh huyền – cạnh góc vuông)
Chọn đáp án A.
Đúng 0
Bình luận (0)
Cho tam giác ABC và tam giác MNP có
A
^
M
^
90
0
,
C
^
P
^
. Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề? A.
A
C
M
P
B.
A
B
M
N
C.
B
C...
Đọc tiếp
Cho tam giác ABC và tam giác MNP có A ^ = M ^ = 90 0 , C ^ = P ^ . Cần điều kiện gì để hai tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề?
A. A C = M P
B. A B = M N
C. B C = N P
D. A C = M N
Ta có: C ^ = P ^ mà góc C và góc P là hai góc nhọn kề của tam giác ABC và tam giác MNP
Do đó để tam giác ABC và tam giác MNP bằng nhau theo trường hợp cạnh góc vuông – góc nhọn kề thì cần thêm điều kiện A C = M P
Đáp án A
Đúng 0
Bình luận (0)
Cho tam giác ABC và tam giác DEF có
A
B
D
E
,
B
^
E
^
,
A
^
D
^
90
0
. Biết
A
C
9
c
m
. Tính độ dài DF? A. 10cm B. 5cm C. 9cm D. 7cm
Đọc tiếp
Cho tam giác ABC và tam giác DEF có A B = D E , B ^ = E ^ , A ^ = D ^ = 90 0 . Biết A C = 9 c m . Tính độ dài DF?
A. 10cm
B. 5cm
C. 9cm
D. 7cm
Cho tam giác ABC ( ∠ A = 90 0 ) có đường cao AH. Chứng minh rằng A H 2 = B H . C H
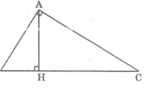
Xét hai tam giác vuông HBA và HAC, ta có:
∠ (AHB) = ∠ (AHC) = 90 0
∠ B = ∠ (HAC) (hai góc cùng phụ C )
Suy ra: △ HBA đồng dạng △ HAC (g.g)
Suy ra: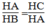 
Vậy A H 2 = B H . C H
Đúng 0
Bình luận (0)
cho tam giác abc có góc A =900 trung tuyển AM=5cm thì cạch huyền BC bằng
Cho tam giác ABC có AB = 3cm, BC = 5cm và B A C ^ = 90 0 . Cho biết tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 1,5cm, hãy tính các cạnh còn lại của tam giác A'B'C'
Tính được AC = 4cm. Sau đó áp dụng cách làm tương tự 3B
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc B và góc C nhỏ hơn 900 . Vẽ ra phía ngoài tam giác ấy các tam giác vuông cân ABD và ACE ( trong đó góc ABD và góc ACE đều bằng 900 ), vẽ DI và EK cùng vuông góc với đường thẳng BC. AH là đường cao của tam giác ABC. Chứng minh rằng: a. BI=AH; EK = HC; b. BC = DI + EK.
Xem chi tiết
Cho tam giác ABC có , biết . Số đo của góc A là: A. 300 B. 600 C.900 D. 1200
Đọc tiếp
Cho tam giác ABC có 
, biết 
. Số đo của góc A là:
A. 300 B. 600 C.900 D. 1200