xin giúp mik vs ạ
LL
Những câu hỏi liên quan
Cho đường tròn tâm O, bán kính R = 10cm. Tam giác ABC nội tiếp đường tròn tâm O, biết góc A là góc tù. Hỏi trong các dây AB, BC và AC thì dây nào gần tâm nhất?
A. AB
B. AC
C. BC
D. Chưa kết luận được
Đáp án C
Tam giác ABC có góc A là góc tù nên 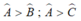
Mà cạnh đối diện với góc A là cạnh BC .
Áp dụng định lí: trong 1 tam giác cạnh đối diện với góc lớn hơn thì lớn hơn ta được:
BC > AC và BC > AB
Vậy tam giác ABC có độ dài cạnh BC là lớn nhất nên dây BC gần tâm nhất.
Chưa thể kết luận dây nào xa tâm nhất.
Đúng 0
Bình luận (0)
Câu1:Cho tam giác ABC,góc A bằng 90°,có cạnh AB 6,tgB4/3.Tính cạnh BC.
Câu2:Cho(O;12cm),một dây cũng của đường tròn tâm O có độ dài bằng bán kính.Tính khoảng cách từ tâm đến dây cũng.
Câu3:Hai đường tròn (O;R)và O;R)d.Biết R12cm,R7cm,d4 thì vị trí tương đối của 2 đường tròn là?
Câu4:Cho hàm số y(2m-1)x+3
a)Tìm m.để HS đi qua điểm A(2;5)
b)Vẽ đths vs m tìm đc ở câu a
Câu5:Cho(O;R),1 đường thẳng d cắt đường tròn (O) tại C,D,lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M.Qua M vẽ tiếp tuyế...
Đọc tiếp
Câu1:Cho tam giác ABC,góc A bằng 90°,có cạnh AB =6,tgB=4/3.Tính cạnh BC. Câu2:Cho(O;12cm),một dây cũng của đường tròn tâm O có độ dài bằng bán kính.Tính khoảng cách từ tâm đến dây cũng. Câu3:Hai đường tròn (O;R)và O';R')=d.Biết R=12cm,R'=7cm,d=4 thì vị trí tương đối của 2 đường tròn là? Câu4:Cho hàm số y=(2m-1)x+3 a)Tìm m.để HS đi qua điểm A(2;5) b)Vẽ đths vs m tìm đc ở câu a Câu5:Cho(O;R),1 đường thẳng d cắt đường tròn (O) tại C,D,lấy điểm M trên đường thẳng d sao cho D nằm giữa C và M.Qua M vẽ tiếp tuyến MA,MB với đường tròn.Gọi H là trung điểm của CD,OM cắt AB tại E.CMR a)AB vuông góc với OM b)Tích OE.OM ko đổi c)Khi M di chuyển trên đường thẳng d thì đường thẳng AB đi qua 1 điểm cố định. (Mọi người giúp e vs ạ)
Câu 1:
Xét ΔABC vuông tại A có
\(tanB=\dfrac{AC}{AB}\)
=>\(\dfrac{AC}{6}=\dfrac{4}{3}\)
=>\(AC=\dfrac{4}{3}\cdot6=8\left(cm\right)\)
Ta có: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Câu 4:
a: Thay x=2 và y=5 vào y=(2m-1)x+3, ta được:
2(2m-1)+3=5
=>2(2m-1)=2
=>2m-1=1
=>2m=2
=>\(m=\dfrac{2}{2}=1\)
b: Khi m=1 thì \(y=\left(2\cdot1-1\right)x+3=x+3\)
Đúng 1
Bình luận (0)
cho đường tròn O bán kính R, dây AB cố định. Điểm M thuộc cung lớn AB. Gọi I là trung điểm của dây AB. Vẽ đường tròn tâm O' qua M tiếp xúc với AB tại A. Tia MI cắt đường tròn tâm o' tại N và cắt đường tròn tâm O tại C. cm NA song sonh với BC?
cho đường tròn O bán kính R, dây AB cố định. Điểm M thuộc cung lớn AB. Gọi I là trung điểm của dây AB. Vẽ đường tròn tâm O' qua M tiếp xúc với AB tại A. Tia MI cắt đường tròn tâm o' tại N và cắt đường tròn tâm O tại C. cm NA song sonh với BC?
Xét (O'): \(O'A\perp AB\) tại A và O'A là bán kính.
\(\Rightarrow\)AB là tiếp tuyến của (O') tại A.
\(\Rightarrow\widehat{NAB}\) là góc tạo bởi tiếp tuyến và dây cung chắn cung AN.
Mặt khác \(\widehat{AMN}\) là góc nội tiếp chắn cung AN.
\(\Rightarrow\widehat{AMN}=\widehat{NAB}\left(1\right)\)
Xét (O): \(\widehat{AMC}=\widehat{ABC}\left(=\dfrac{1}{2}sđ\stackrel\frown{AC}\right)\left(2\right)\)
\(\left(1\right),\left(2\right)\Rightarrow\widehat{NAB}=\widehat{ABC}\) nên AN//BC.
Đúng 2
Bình luận (0)
cho đường tròn (o;R) và một điểm A sao cho Oa2R vẽ tiếp tuyến AB với đường tròn tâm o (b là tiếp tuyến ) vẽ dây Bc của đường tròn tâm o vuông góc với OA tại Ha) tính Ab theo R và chứng minh Ac là tiếp tuyến của đường tròn tâm Ob) c/m tam giác abc là tam giác đềuc) trên tia đối của tia BC lấy điểm Q. từ Q vẽ 2 tiếp tuyến QD vad QE của đường tròn tâm O ( D và E là 2 tiếp tuyến ). C/M 2 điểm A,E,D thẳng hàng
Đọc tiếp
cho đường tròn (o;R) và một điểm A sao cho Oa=2R vẽ tiếp tuyến AB với đường tròn tâm o (b là tiếp tuyến ) vẽ dây Bc của đường tròn tâm o vuông góc với OA tại H
a) tính Ab theo R và chứng minh Ac là tiếp tuyến của đường tròn tâm O
b) c/m tam giác abc là tam giác đều
c) trên tia đối của tia BC lấy điểm Q. từ Q vẽ 2 tiếp tuyến QD vad QE của đường tròn tâm O ( D và E là 2 tiếp tuyến ). C/M 2 điểm A,E,D thẳng hàng
Cho đường tròn (O ; R) và dây cung BC cố định ( BC 2R). Điểm A di động trên đường tròn (O ; R ) sao cho ΔABC nhọn. Gọi AD , BP và CQ là các đường cao, H là trực tâm của Δ ABC.a) C/m : APHQ nội tiếp đường tròn. Xác định tâm Xb) Gọi T là trung điểm của BC.C/m : TP là tiếp tuyến của (X)c) Hạ DE, DF lần lượt vuông góc với BP, CQ.C/m : EF // PQ(Mình đang cần gấp)
Đọc tiếp
Cho đường tròn (O ; R) và dây cung BC cố định ( BC < 2R). Điểm A di động trên đường tròn (O ; R ) sao cho ΔABC nhọn. Gọi AD , BP và CQ là các đường cao, H là trực tâm của Δ ABC.
a) C/m : APHQ nội tiếp đường tròn. Xác định tâm X
b) Gọi T là trung điểm của BC.
C/m : TP là tiếp tuyến của (X)
c) Hạ DE, DF lần lượt vuông góc với BP, CQ.
C/m : EF // PQ
(Mình đang cần gấp)
Cho đường tròn tâm O bán kính R dây AB không đi qua tâm . Vẽ dây VC vông góc với AB
a, Chứng minh AC là đường kính của đường tròn O
b, Tính R biết AB =12 , BC = 5
Trrinfh bày cách làm nữa nha
cho đường tròn O;R cố định và dây BC cố định . trên BC lấy A cố định. M là điểm thay đổi trên đường tròn O . Cm trọng tâm G của Mac luôn nằm trên 1 đường tròn cố định
cho nửa đường tròn tâm o đường kính bc . tính độ dài AC và số đo góc của tam giác ABC biêt a) Dây AB=R√3 b) Dây AB=R√2
cho đường tròn tâm O, bán kính R, dây cung AB=R. TRên tia đối của tia BA lấy C sao cho BC=BA. Tia CO cắt đường tròn tâm O tại D. R=3 cm
a, tính góc ACD
b, tính CD
Đề không nói rõ là đoạn thẳng OC cắt đường tròn hay đường thẳng OC. Vì nếu là đường thăng thì sẽ có hai điểm D. Ta coi D là giao điểm của đoạn thẳng OC với đường tròn, nếu D là giao của tia đối của tia OC với đường tròn thì chỉ việc cộng thêm 2R.
Tam giác OAB có \(OA=OB=AB=R\to\Delta OAB\) đều. Suy ra \(\angle OBA=60^{\circ}.\) Do \(BC=BA=OB=R\to\Delta BCO\) cân ở B. Vậy theo tính chất góc ngoài tam giác \(\angle OBA=\angle BOC+\angle BCO=2\angle BCO\to\angle BCO=\frac{60^{\circ}}{2}=30^{\circ}.\) Vậy góc ACD bằng 30 độ.
Kẻ OH vuông góc với AB. Vì tam giác OAB đều nên \(OH=\frac{\sqrt{3}}{2}AB=\frac{\sqrt{3}}{2}R=\frac{3\sqrt{3}}{2}.\) Tam giác OHC vuông ở H có góc đỉnh C bằng 30 độ nên \(OH=\frac{1}{2}OC\to OC=2\times\frac{3\sqrt{3}}{2}=3\sqrt{3}.\) Mà \(OD=R=3\to CD=OC-OD=3\sqrt{3}-3.\)
Đúng 0
Bình luận (0)





