Cho \(\Delta ABC\) có ba cạnh tương ứng là a; b; c
thỏa mãn \(a^3+b^3+c^3=3abc\) Hỏi \(\Delta ABC\) là tam giác gì
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho \(\Delta ABC=\Delta HIK\)
a) Tìm cạnh tương ứng với cạnh BC. Tìm góc tương ứng với góc H
b) Tìm các cạnh bằng nhau, tìm các góc bằng nhau
a) Vì \(\Delta ABC=\Delta HIK\)
nên BC = IK (2 cạnh t/ư)
và \(\widehat{A}=\widehat{H}\) (2 góc t/ư)
b) Do \(\Delta ABC=\Delta HIK\)
=> AB = HI; AC = HK (2 cạnh t.ư); BC = IK (câu a)
và \(\widehat{A}=\widehat{H}\) (câu a); \(\widehat{B}=\widehat{I}\) và \(\widehat{C}=\widehat{K}\) (2 góc t/ư).
a) Ta có \(\Delta\) ABC= \(\Delta\)HIK, nên cạnh tương ứng với BC là cạnh IK
góc tương ứng với góc H là góc A.
b) \(\Delta\) ABC= \(\Delta\)HIK
Suy ra: AB=HI, AC=HK, BC=IK.
\(\widehat{A}=\widehat{H};\widehat{B}=\widehat{I};\widehat{C}=\widehat{K}\)
a, Vì tam giác ABC bằng tam giác HIK nên BC=IK(2 cạnh t/ư)
và góc A=góc H(2 góc t/ư)
b,Do tam giác ABC = tam giác HIK
suy ra:AB = HI, AC = HK(2 cạnh tương ứng), BC = IK(theo phần a) và góc A = góc H, gíc B = góc I, góc C= góc K
a) Trong Hình 11, cho biết \(\Delta ABC\backsim\Delta A'B'C'\). Viết tỉ số của các cạnh tương ứng và chỉ ra các cặp góc tương ứng.

b) Trong Hình 12, cho biết \(\Delta DEF\backsim\Delta D'E'F'\). Tính số đo \(\widehat {D'}\) và \(\widehat F\).
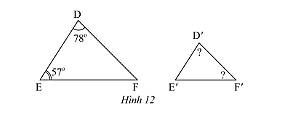
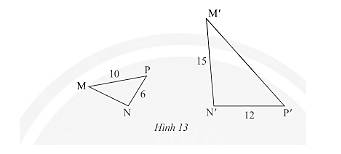
c) Trong Hình 12, cho biết \(\Delta MNP\backsim\Delta M'N'P'\). Tính độ dài các đoạn thẳng \(MN\) và \(MP'\).
a) Ta có: \(\Delta ABC\backsim\Delta A'B'C'\) thì \(\left\{ \begin{array}{l}\widehat A = \widehat {A'};\widehat B = \widehat {B'};\widehat C = \widehat {C'}\\\frac{{A'B'}}{{AB}} = \frac{{A'C'}}{{AC}} = \frac{{B'C'}}{{BC}} = k\end{array} \right.\).
b) Xét tam giác \(DEF\) có:
\(\widehat D + \widehat E + \widehat F = 180^\circ \) (tổng ba góc trong một tam giác).
Ta có: \(\widehat D = 78^\circ ;\widehat E = 57^\circ \) thay số ta được
\(78^\circ + 57^\circ + \widehat F = 180^\circ \Rightarrow \widehat F = 180^\circ - 78^\circ - 57^\circ = 45^\circ \)
Ta có: \(\Delta DEF\backsim\Delta D'E'F' \Rightarrow \widehat D = \widehat {D'};\widehat E = \widehat {E'};\widehat F = \widehat {F'}\) (các góc tương ứng bằng nhau)
Do đó, \(\widehat D = \widehat {D'} = 78^\circ ;\widehat F = \widehat {F'} = 45^\circ \).
c) Ta có \(\Delta MNP\backsim\Delta M'N'P' \Rightarrow \frac{{MN}}{{M'N'}} = \frac{{MP}}{{M'P'}} = \frac{{NP}}{{N'P'}}\) (các cặp cạnh tương ứng có cùng tỉ lệ).
Với \(MP = 10;NP = 6;M'N' = 15;N'P' = 12\) thay vào ta được:
\( \Rightarrow \left\{ \begin{array}{l}\frac{{MN}}{{15}} = \frac{1}{2}\\\frac{{10}}{{M'P'}} = \frac{1}{2}\end{array} \right. \Rightarrow \left\{ \begin{array}{l}MN = \frac{{15.1}}{2} = 7,5\\M'P' = \frac{{10.2}}{1} = 20\end{array} \right.\).
Vậy \(MN = 7,5;M'P' = 20\).
Cho \(\Delta ABC\) có diện tích S, bán kính đường tròn ngoại tiếp là R và \(\Delta ABC\) có các cạnh tương ứng là a,b,c. CMR: S = \(\frac{abc}{4R}\)
cho \(\Delta ABC.\)độ dài 3 cạnh của tam giác tỉ lệ vs 2:3:4.ba chiều cao tương ứng vs 3 cạnh đó tr lệ vs 3 số nào
gọi 3 cạnh của Δlà a,b,c (a,b,c >0)
3 chiều cao của Δ là x,y,z (x,y,z>0)
ta có : \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}\)
đặt \(\frac{a}{2}=\frac{b}{3}=\frac{c}{4}=k\left(k>0\right)\)
\(\Rightarrow\)a=2k ;b=3k ; c=4k
ta có : 2S=a.x=b.y=c.z=2k.x=3k.y=4k.z ( S là diện tích )
\(\Rightarrow2x=3y=4z\Rightarrow\frac{2x}{12}=\frac{3y}{12}=\frac{4z}{12}\Rightarrow\frac{x}{6}=\frac{y}{4}=\frac{z}{3}\)
vậy 3 chiều cao tương ứng tỉ lệ vs 6;4;3
cho tam giác ABC có độ dài ba cạnh là a,b,c sao cho (a+2b)/5 = (b+2c)/7 = (c+2a)/9. Tìm tỉ lệ của ba đường cao tương ứng
Quan sát Hình 3, cho biết \(\Delta AMN\backsim\Delta ABC\).
a) Hãy viết tỉ số của các cạnh tương ứng và tính tỉ số đồng dạng.
b) Tính góc \(\widehat {AMN}\).
a) Vì tam giác \(\Delta AMN\backsim\Delta ABC\) nên ta có \(\frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\) (các cạnh tương ứng)
Tỉ số đồng dạng là: \(\frac{{MN}}{{BC}} = \frac{4}{{12}} = \frac{1}{3}\).
b) Vì \(\Delta AMN\backsim\Delta ABC\) nên \(\widehat {AMN} = \widehat {ABC} = 65^\circ \)
Vậy \(\widehat {AMN} = 65^\circ \).
a: AM/AB=AN/AC=MN/BC=4/12=1/3
b: góc AMN=góc ABC=65 độ
B4: Cho\(\Delta\)ABC = \(\Delta\)HIK
a) Tìm cạnh tương ứng vs AC. Tìm góc tương úng vs góc I.
b) Tìm các cạnh bằng nhau và các góc bàng nhau
a) Cạnh tương ứng với AC là HK
Góc tương ứng với góc I là góc B
b) Các cạnh bằng nhau: AB = HI ; BC = IK; AC = HK
Các góc bằng nhau: góc A = góc H; góc B = góc I; góc C = góc K
xét \(\Delta ABC\) và \(\Delta HIK\)
a) cạnh tương ứng với cạnh \(AC\)là \(HK\)
góc tương ứng với góc \(I\)là góc \(B\)
b) các cạnh = nhau: \(AB=HI\); \(AC=HK\); \(BC=IK\)
các góc = nhau \(\widehat{A}=\widehat{H}\); \(\widehat{B}=\widehat{I}\); \(\widehat{C}=\widehat{K}\)
\(\Delta ABC=\Delta A'B'C'\)
Các cạnh tương ứng ?
Các góc tương ứng?
Các đỉnh tương ứng?
TRả lời để bấm đúng
Cho tam giác vuông ABC vuông tại A. Biết độ dài ba cạnh là: AB=6cm, AC=8cm và BC=10cm. Tính chiều cao tương ứng với cạnh đáy BC
Gọi AH là cc tương ứng với BC
Áp dụng HTL: \(AH=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\)