Cho hình bình hành ABCD, một đường thẳng d cắt các cạnh AB và AD lần lượt tại M và K; cắt đường chéo AC tại G. Chứng minh rằng: \(\frac{AB}{AM}+\frac{AD}{AK}=\frac{AC}{AG}.\)
KS
Những câu hỏi liên quan
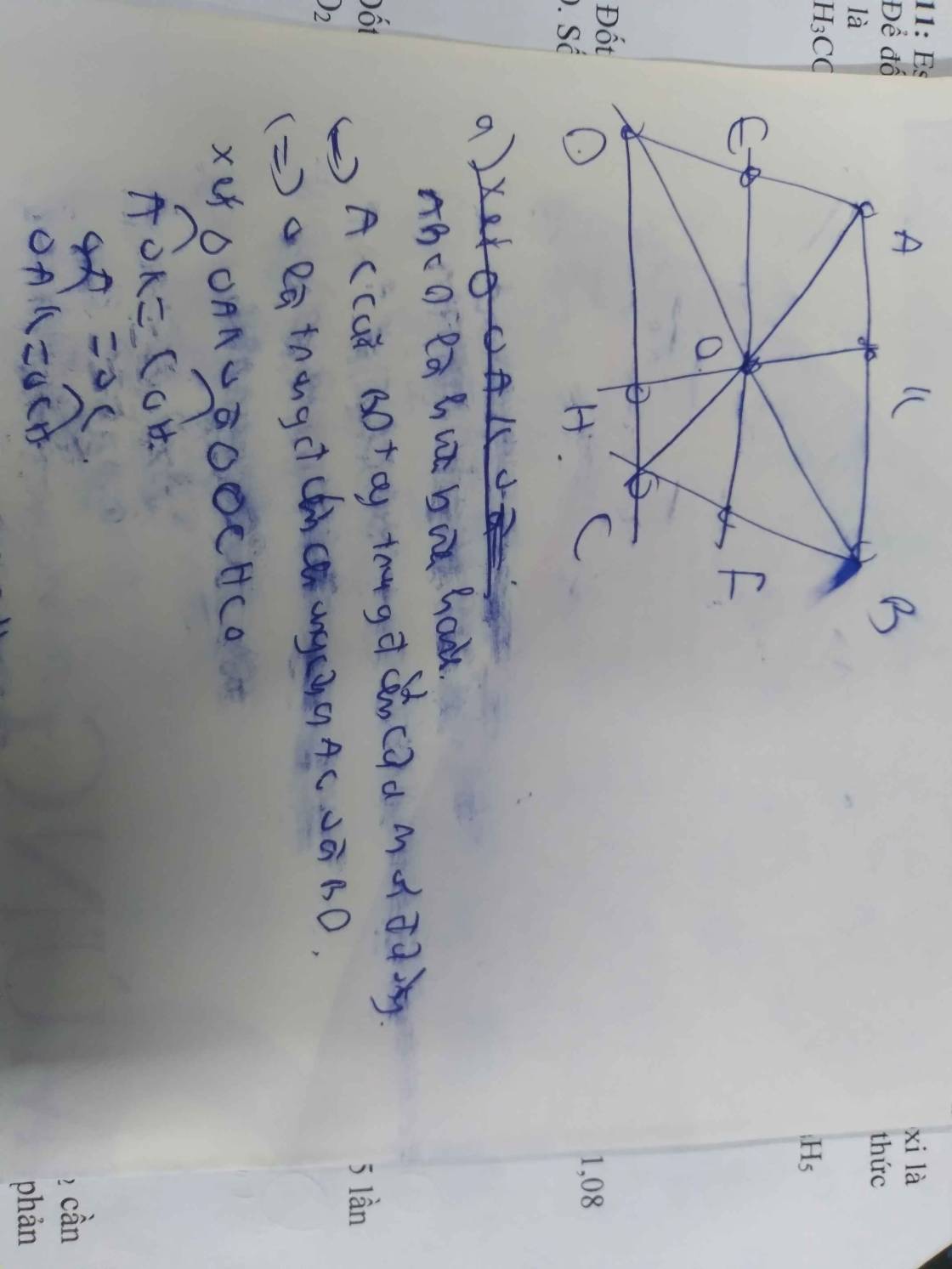
Cho hình bình hành ABCD (góc A nhỏ hớn 90 độ), lấy điểm M trên BD sao cho MB < MD. Đường thẳng qua M và song song với AB cắt AD và BC lần lượt tại E và F. Đường thẳng qua M song song với AD cắt AB và AC lần lượt tại K và H.
1. Chứng minh: các đường thẳng EK, HF, BD đồng quy
2. Cho SMKF = 9 cm2 ; SMEH = 25 cm2 . Tính SABCD.
Đề sai rồi, em kiểm tra lại, EK, HF và BD ko hề đồng quy
Đúng 2
Bình luận (0)
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB < MD. Đường thẳng qua M và song song với AB cắt AD và BC lần lượt tại E và F. Đường thẳng qua M song song với AD cắt AB và AC lần lượt tại K và H.
1. Chứng minh: các đường thẳng EK, HF, BD đồng quy
2. Cho SMKF = 9 cm2 ; SMEH = 25 cm2 . Tính SABCD.
Đúng 0
Bình luận (2)
Đặt tên các điểm như hình vẽ.
Các tứ giác AEMK, BKMF, CFMH, DHME đều là hình bình hành (hai căpj cạnh đối song song theo giả thiết)
\(\Rightarrow MK=BF\) ; \(EF=CD\); \(MH=BC\)
Áp dụng định lý Talet cho tam giác BCD: \(\dfrac{BF}{BC}=\dfrac{MF}{CD}\) \(\Rightarrow\dfrac{MK}{MH}=\dfrac{MF}{EF}\)
\(\Rightarrow KF||EH\) (Talet đảo)
\(\Rightarrow KFHE\) là hình thang
Gọi G là giao điểm EK và HF, theo bổ đề hình thang do M là giao điểm 2 đường chéo hình thang \(\Rightarrow MG\) đi qua trung điểm I và J của 2 đáy KF và EH hay G, M, I, J thẳng hàng
Mặt khác BKMF và DEMH là hbh \(\Rightarrow B;I;M\) và \(D;J;M\) thẳng hàng \(\Rightarrow B;D;I;J;M\) thẳng hàng (do \(I;J;M\) thẳng hàng)
\(\Rightarrow B;D;G\) thẳng hàng
Hay EK, HF, BD đồng quy tại G
b.
Từ E và H hạ vuông góc xuống KF tại L và N
\(\Rightarrow ELNH\) là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông) \(\Rightarrow EL=HN\)
\(S_{EFK}=\dfrac{1}{2}EL.KF\) ; \(S_{HFK}=\dfrac{1}{2}HN.KF\)
\(\Rightarrow S_{EFK}=S_{HFK}\Rightarrow S_{EMK}+S_{MFK}=S_{HFM}+S_{MFK}\)
\(\Rightarrow S_{EMK}=S_{HMF}\Rightarrow\dfrac{1}{2}S_{AEMK}=\dfrac{1}{2}S_{SFMH}\Rightarrow S_{AEMK}=S_{SFMH}\)
Hai tam giác MKF và MEH đồng dạng (g.g) \(\Rightarrow\dfrac{S_{MFK}}{S_{MHE}}=\left(\dfrac{MF}{ME}\right)^2=\dfrac{9}{25}\)
\(\Rightarrow\dfrac{MF}{ME}=\dfrac{3}{5}\)
Từ K kẻ KO vuông góc EF
\(\Rightarrow\dfrac{S_{EMK}}{S_{MFK}}=\dfrac{\dfrac{1}{2}KO.ME}{\dfrac{1}{2}KO.MF}=\dfrac{ME}{MF}=\dfrac{5}{3}\)
\(\Rightarrow S_{EMK}=\dfrac{5}{3}.9=15\left(cm^2\right)\)
\(\Rightarrow S_{ABCD}=2.9+2.25+4.15=128\left(cm^2\right)\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.a, CM: BK.MDBM.KA.b, CM: KF//EH.c, CM: EK, HF, BD đồng quy.d, CM: SMKAESMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.a, CM: BK...
Đọc tiếp
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.c
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB khác MD. Đường thẳng qua M và song song với AB cắt Ad và BC lần lượt tại E và F. Đường thẳng qua M và song song với AD cắt AB và CD lần lượt tại K và H.
a, CM: BK.MD=BM.KA.
b, CM: KF//EH.
c, CM: EK, HF, BD đồng quy.
d, CM: SMKAE=SMHCF.
hỏi từ từ thôi hỏi như này bao giờ trả lời xong
Sao bạn hỏi nhiều vậy bạn
Nhìn đã thấy nản
Xem thêm câu trả lời
. Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Qua điểm O, vẽ đường thẳng a cắt hai đường thẳng AD, BC lần lượt tại E, F, vẽ đường thẳng b cắt hai cạnh AB, CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành
Đọc tiếp
. Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Qua điểm O, vẽ đường thẳng a cắt hai đường thẳng AD, BC lần lượt tại E, F, vẽ đường thẳng b cắt hai cạnh AB, CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành
ABCD là hình bình hành
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
Xét ΔOAK và ΔOCH có
\(\widehat{OAK}=\widehat{OCH}\)(hai góc so le trong, AK//CH)
OA=OC
\(\widehat{AOK}=\widehat{COH}\)(hai góc đối đỉnh)
Do đó: ΔOAK=ΔOCH
=>OK=OH
=>O là trung điểm của KH
Xét ΔOAE và ΔOCF có
\(\widehat{EAO}=\widehat{FCO}\)(hai góc so le trong, AE//CF)
OA=OC
\(\widehat{AOE}=\widehat{COF}\)
Do đó: ΔOAE=ΔOCF
=>OE=OF
=>O là trung điểm của EF
Xét tứ giác EKFH có
O là trung điểm chung của EF và KH
=>EKFH là hình bình hành
Đúng 0
Bình luận (0)
Cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD. Qua điểm O, vẽ đường thẳng a cắt hai đường thẳng AD, BC lần lượt tại E, F. Qua O vẽ đưòng thẳng b cắt hai cạnh AB, CD lần lượt tại K, H. Chứng minh tứ giác EKFH là hình bình hành
Ta có DAOK = DCOH Þ OK =OH, DDOE = DBOF Þ OE = OF Þ EHFK là hình bình hành

Đúng 1
Bình luận (1)
cho hình bình hành abcd. gọi o là giao điểm hai đường chéo ac và bd. qua điểm o, vẽ đường thẳng d cắt hai đường thẳng ad, bc lần lượt tại e, f. qua o vẽ đưòng thẳng d' cắt hai cạnh ab, cd lần lượt tại k, h.
a cm akch và aecf là hbh
b cm ekfh là hbh
Vẽ hộ mình cái hình nhe
cho hình bình hành ABCD. Gọi O là giao điểm hai đường chéo AC và BD. qua điểm O, vẽ đường thẳng a cắt hai đường thẳng AD,BC lần lượt tại E,F. Qua O vẽ đường thẳng b cắt hai cạnh AB<CD LẦn lượt tại K,H. chứng mih tứ giác EKFH là hình bình hành
ABCD là hbh=> AD//BC=> góc DAC= góc ACB và AO=OC
Xét tam giác AOE và tam giác COF ta có
góc AOE = góc COF (2 góc đối xừng)
AO=OC
góc DAC= góc ACB
=> tam giác AOE = tam giác COF=> OE=OF
CHứng minh tương tự ta có tam giác AOK= tam giác COH=> OK=OH
Xét tứ giác EHFK có EH và FK là 2 đường chéo cắt nhau tại O
lại có OE=OF
OH=OK
=> EHFk là hình bình hành (do 2 đường chéo cắt nhau tại trung điểm mỗi đường)
Đường thẳng d cắt các cạnh AB, AD và đường chéo AC của hình bình hành ABCD lần lượt tại E, F và O.
Chứng minh rằng ::AB/AE++AD/AF=AC/AO
Qua B và D kẻ 2 đường thẳng song song với d cắt đường chéo AC của hbh ABCD tại H và K.
Gọi I là tâm đối xứng của hbh ABCD.
Áp dụng ĐL Thales ta có các tỉ số: \(\frac{AB}{AE}=\frac{AH}{AO};\frac{AD}{AF}=\frac{AK}{AO}\)
\(\Rightarrow\frac{AB}{AE}+\frac{AD}{AF}=\frac{AH+AK}{AO}=\frac{2AK+IH+IK}{AO}\)(*)
Dễ thấy \(\Delta\)BHI=\(\Delta\)DKI (g.c.g) => IH=IK, thay vào (*)
\(\Rightarrow\frac{AB}{AE}+\frac{AD}{AF}=\frac{2AK+2IK}{AO}=\frac{2\left(AK+IK\right)}{AO}=\frac{2AI}{AO}\)
Mà AI=1/2AC => \(\frac{AB}{AE}+\frac{AD}{AF}=\frac{AC}{AO}\)(đpcm).
Đúng 0
Bình luận (0)
cho hình bình hành ABCD vè đường thẳng d cắt cạnh AB,AD tại M và K cắt đường chéo AC tại G. Chứng minh rằng : AB/AM+AD/AK=AC/AG
Cho hình bình hành ABCD gọi O la giao điểm của hai đường chéo AC và BD. Qua O vẽ đường thẳng a cắt 2 đường thẳng AD và BC lần lượt tại E, F; vẽ đường thẳng b cắt 2 đường thẳng AB và BD lần lượt tại K, H. Chứng minh EKFH là hình bình hành
bài đó cũng khó nhỉ hehehehe