Cho hình bình hành ABCD (góc A nhỏ hớn 90 độ), lấy điểm M trên BD sao cho MB < MD. Đường thẳng qua M và song song với AB cắt AD và BC lần lượt tại E và F. Đường thẳng qua M song song với AD cắt AB và AC lần lượt tại K và H.
1. Chứng minh: các đường thẳng EK, HF, BD đồng quy
2. Cho SMKF = 9 cm2 ; SMEH = 25 cm2 . Tính SABCD.
Đề sai rồi, em kiểm tra lại, EK, HF và BD ko hề đồng quy
Cho hình bình hành ABCD, lấy điểm M trên BD sao cho MB < MD. Đường thẳng qua M và song song với AB cắt AD và BC lần lượt tại E và F. Đường thẳng qua M song song với AD cắt AB và AC lần lượt tại K và H.
1. Chứng minh: các đường thẳng EK, HF, BD đồng quy
2. Cho SMKF = 9 cm2 ; SMEH = 25 cm2 . Tính SABCD.
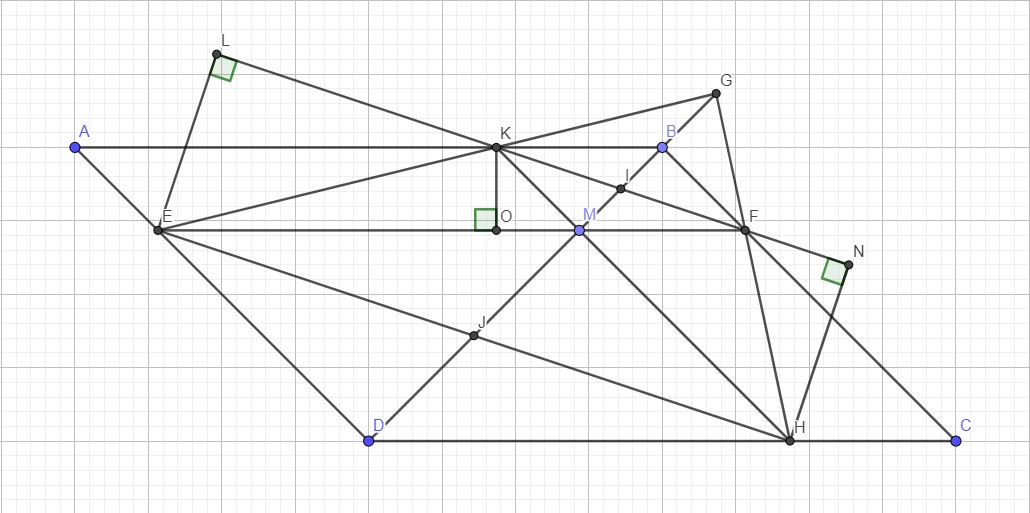
Đặt tên các điểm như hình vẽ.
Các tứ giác AEMK, BKMF, CFMH, DHME đều là hình bình hành (hai căpj cạnh đối song song theo giả thiết)
\(\Rightarrow MK=BF\) ; \(EF=CD\); \(MH=BC\)
Áp dụng định lý Talet cho tam giác BCD: \(\dfrac{BF}{BC}=\dfrac{MF}{CD}\) \(\Rightarrow\dfrac{MK}{MH}=\dfrac{MF}{EF}\)
\(\Rightarrow KF||EH\) (Talet đảo)
\(\Rightarrow KFHE\) là hình thang
Gọi G là giao điểm EK và HF, theo bổ đề hình thang do M là giao điểm 2 đường chéo hình thang \(\Rightarrow MG\) đi qua trung điểm I và J của 2 đáy KF và EH hay G, M, I, J thẳng hàng
Mặt khác BKMF và DEMH là hbh \(\Rightarrow B;I;M\) và \(D;J;M\) thẳng hàng \(\Rightarrow B;D;I;J;M\) thẳng hàng (do \(I;J;M\) thẳng hàng)
\(\Rightarrow B;D;G\) thẳng hàng
Hay EK, HF, BD đồng quy tại G
b.
Từ E và H hạ vuông góc xuống KF tại L và N
\(\Rightarrow ELNH\) là hình chữ nhật (2 cặp cạnh đối song song và 1 góc vuông) \(\Rightarrow EL=HN\)
\(S_{EFK}=\dfrac{1}{2}EL.KF\) ; \(S_{HFK}=\dfrac{1}{2}HN.KF\)
\(\Rightarrow S_{EFK}=S_{HFK}\Rightarrow S_{EMK}+S_{MFK}=S_{HFM}+S_{MFK}\)
\(\Rightarrow S_{EMK}=S_{HMF}\Rightarrow\dfrac{1}{2}S_{AEMK}=\dfrac{1}{2}S_{SFMH}\Rightarrow S_{AEMK}=S_{SFMH}\)
Hai tam giác MKF và MEH đồng dạng (g.g) \(\Rightarrow\dfrac{S_{MFK}}{S_{MHE}}=\left(\dfrac{MF}{ME}\right)^2=\dfrac{9}{25}\)
\(\Rightarrow\dfrac{MF}{ME}=\dfrac{3}{5}\)
Từ K kẻ KO vuông góc EF
\(\Rightarrow\dfrac{S_{EMK}}{S_{MFK}}=\dfrac{\dfrac{1}{2}KO.ME}{\dfrac{1}{2}KO.MF}=\dfrac{ME}{MF}=\dfrac{5}{3}\)
\(\Rightarrow S_{EMK}=\dfrac{5}{3}.9=15\left(cm^2\right)\)
\(\Rightarrow S_{ABCD}=2.9+2.25+4.15=128\left(cm^2\right)\)