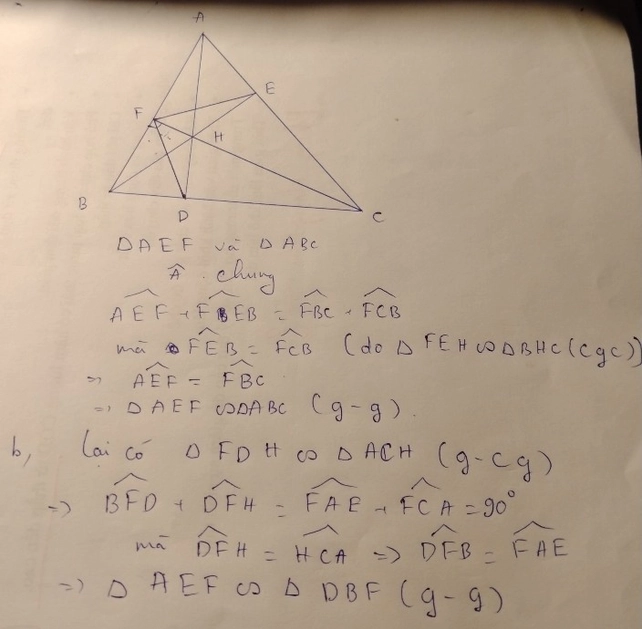cho tam giác ABC biết các đường trung tuyến xuất phát tại các đỉnh A và B lần lượt bằng 3cm, 3,6cm; cạnh BC=4cm. tính diện tích tam giác ABC và tính hai cạnh còn lại của tam giác ABC
AM
Những câu hỏi liên quan
1. Cho tam giác ABC. Gọi O là giao điểm của hai đường xuất phát từ hai đỉnh B và C của tam giác ABC. Chứng minh rằng AO là tia phan giác của góc A
2. Cho tam giác ABC cân tại A. Gọi G, O lần lượt là giao điểm của ba đường trung tuyến, ba đường trung trực của tam giác đó.. Chứng minh rằng A,G,O thẳng hàng
cho tam giác abc đồng dạng với tam giác a'b'c' gọi ah ad am lần lượt là đường cao phân giác trung tuyến xuất phát từ dỉnh a của tam giác abc ah' ad' am' lần lượt là đường cao phân giác trung tuyến xuất phát từ dỉnh a của tam giác a'b'c' chứng minh ràng tam giác abh đồng dạng vớ tam giác a'b'h'
Vẽ tam giác ABC cân tại A vẽ các đường trung tuyến,đường phan giác,đường trung trực xuất phát từ đỉnh A tới cạnh đối diện rút ra nhận xét
Chưa học nên chưa biết, xin lỗi bạn nhé tớ chưa học dạng toán hình học này!
Đúng 0
Bình luận (0)
Ta thấy các đường trung tuyến đường phân giác, đường trung trực xuất phát từ A tới cạnh đối diện trùng nhau .
Đúng 1
Bình luận (0)
Các đường trung tuyến, đường phân giác và đường trung trực xuất phát từ đỉnh A đến cạnh đối diện trùng nhau
Đúng 0
Bình luận (0)
Cho tam giác nhọn ABC cân tại đỉnh A. Hai đường cao xuất phát từ đỉnh B và đỉnh C cắt nhau tại M. Hãy tìm các góc của tam giác ABC, biết ∠(BMC) = 140o.
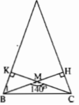
+) Xét tam giác vuông BKM có ∠BMC là góc ngoài tam giác tại đỉnh M nên:

Đúng 0
Bình luận (0)
Trong mặt phẳng hệ tọa độ oxy, cho tam giác ABC có đỉnh A nằm trên trục õ với 0<xa<2,5. Các đường cao xuất phát từ B và C lần lượt có pt d1:x-y+1=0 à d2:2x+y-4=0. Tìm tọa độ các đỉnh A,B,C sao cho diện tích tam giác ABC bằng 6,75
Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng
a)\(AI < \dfrac{1}{2}\left( {AB + AC} \right)\)
b)\(AM < \dfrac{1}{2}\left( {AB + AC} \right)\)
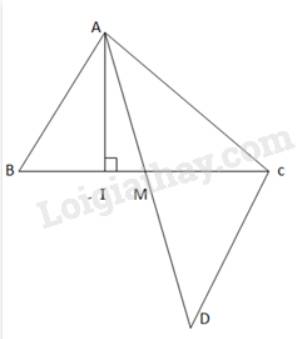
a)
AI là đường vuông góc kẻ từ A xuống đoạn thẳng BC.
\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}AI < AB\\AI < AC\end{array} \right.\\ \Rightarrow 2AI < AB + AC\\ \Rightarrow AI < \dfrac{1}{2}\left( {AB + AC} \right)\end{array}\) (đường vuông góc nhỏ hơn đường xiên)
b)
Lấy D sao cho M là trung điểm của AD
Xét \(\Delta ABM\) và \(DCM\) có
AM = DM ( do M là trung điểm của AD)
BM = CM ( do M là trung điểm của BC)
\(\widehat {AMB} = \widehat {CMD}\)( 2 góc đối đỉnh)
\( \Rightarrow \Delta ABM = \Delta DCM\left( {c - g - c} \right)\)
\( \Rightarrow AB = CD\)(2 cạnh tương ứng)
Xét \(\Delta ADC\) ta có: AD < AC + CD (bất đẳng thức tam giác)
\( \Rightarrow \) 2AM < AC + AB
\( \Rightarrow \) AM < \(\dfrac{1}{2}\)(AB + AC)
Đúng 0
Bình luận (0)
Nối các đỉnh B và C của tam giác ABC cân tại A với trung tuyến O của đường cao AH . Các đường thẳng này lần lượt cắt AC , ABtai D , E . Tính diện tích tứ giác AEOD theo diện tích ABC
Cho tam giác ABC cân tại A.
a. Kẻ đường trung tuyến AM (M thuộc BC).
b. Chứng minh rằng AM là đường phân giác xuất phát từ đỉnh A của tam giác ABC.
a: 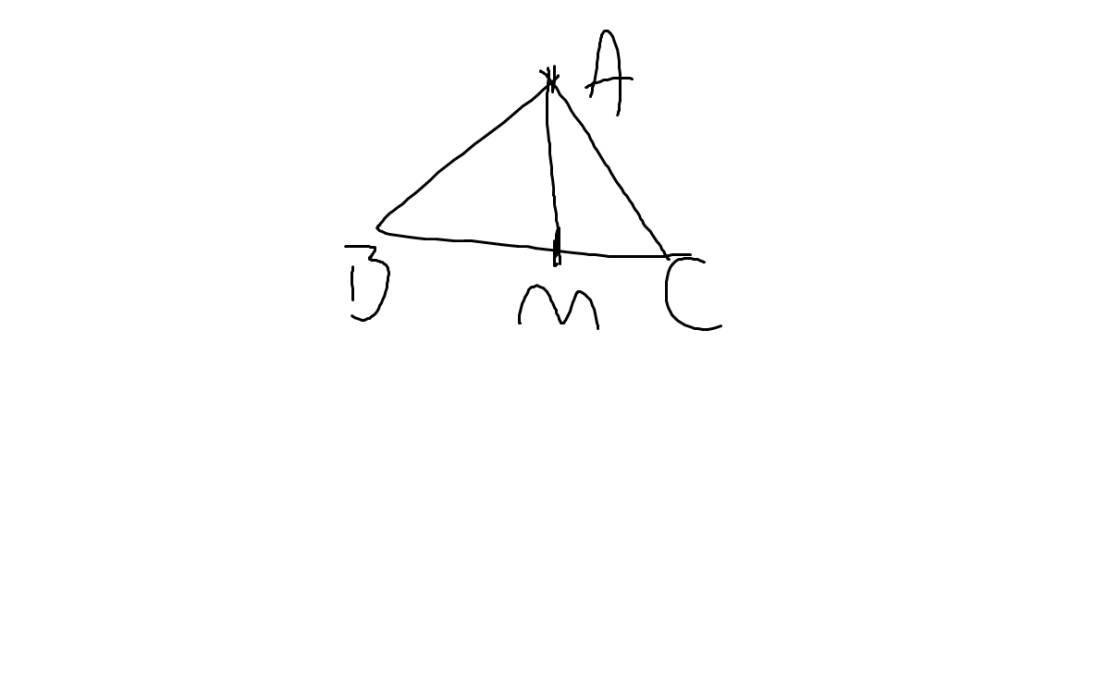
b: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
=>ΔABM=ΔACM
=>góc BAM=góc CAM
=>AM là phân giác của góc BAC
Đúng 0
Bình luận (0)
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJSABI+SCBJBài 3: Cho tam giác ABC có AB3cm, BC4cm, CA5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tí...
Đọc tiếp
Bài 1: Cho tam giác ABC cân ở A. Các đường thẳng qua đỉnh B,C và trung điểm O của đường cao tương ứng với đỉnhA cắt các cạnh AB, AC tương ứng tại M, N. Biết diện tích tam giác ABC bằng S, tính diện tích tứ giác AMON?
Bài 2: Cho tứ giác ABCD, M và N lần lượt là trung điểm của BC và AD. AM cắt BN ở I, DM cắt CN ở J. Chứng minh rằng: SMINJ=SABI+SCBJ
Bài 3: Cho tam giác ABC có AB=3cm, BC=4cm, CA=5cm. Đường cao, đường phân giác, đường trung tuyến của tam giác ABC kẻ từ đỉnh B chia tam giác thành 4 phần. Tính diện tích mỗi phần?
Bài 4: Cho tam giác ABC có diện tích 30cm2. trên cạnh AB lấy điểm D sao cho AD=2DB, trên cạnh AC lấy điểm E sao cho AE=3EC. Gọi M là giao điểm của BE và CD. Tính diện tích tam giác AMB?