Question

Gọi AI và AM lần lượt là đường cao và đường trung tuyến xuất phát từ đỉnh A của tam giác ABC. Chứng minh rằng

a)\(AI < \dfrac{1}{2}\left( {AB + AC} \right)\)

b)\(AM < \dfrac{1}{2}\left( {AB + AC} \right)\)

Answer 1

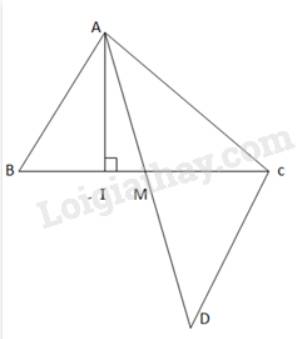
a)

AI là đường vuông góc kẻ từ A xuống đoạn thẳng BC.

\(\begin{array}{l} \Rightarrow \left\{ \begin{array}{l}AI < AB\\AI < AC\end{array} \right.\\ \Rightarrow 2AI < AB + AC\\ \Rightarrow AI < \dfrac{1}{2}\left( {AB + AC} \right)\end{array}\) (đường vuông góc nhỏ hơn đường xiên)

b)

Lấy D sao cho M là trung điểm của AD

Xét \(\Delta ABM\) và \(DCM\) có

AM = DM ( do M là trung điểm của AD)

BM = CM ( do M là trung điểm của BC)

\(\widehat {AMB} = \widehat {CMD}\)( 2 góc đối đỉnh)

\( \Rightarrow \Delta ABM = \Delta DCM\left( {c - g - c} \right)\)

\( \Rightarrow AB = CD\)(2 cạnh tương ứng)

Xét  \(\Delta ADC\) ta có: AD < AC + CD (bất đẳng thức tam giác)

\( \Rightarrow \)   2AM < AC + AB

\( \Rightarrow \)   AM < \(\dfrac{1}{2}\)(AB + AC)