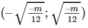Xét sự biến thiên và vẽ đồ thị hàm số sau: a. y=2x2 -4x+1; b. y=-x2 + 4x
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Khảo sát sự biến thiên và vẽ đồ thị hàm số:
a) y= x4+2x2-3
b) y= -x4-4x-1
Xét sự biến thiên và vẽ đồ thị của các hàm số sau:
a) y=x2-2x
c) y=2x2+6x+3
Cho P: y=ax2+bx+1. Tìm a,b để:
(P) đi qua B(-1;6) và có tung độ đỉnh là -3.
Bài 2:
Ta có: \(\dfrac{-\text{Δ}}{4a}=-3\)
\(\Leftrightarrow-\text{Δ}=-12a\)
\(\Leftrightarrow b^2-4a=12a\)
\(\Leftrightarrow b^2-16a=0\left(1\right)\)
Thay x=-1 và y=6 vào (P), ta được:
\(a\cdot\left(-1\right)^2+b\left(-1\right)+1=6\)
\(\Leftrightarrow a-b=5\)
\(\Leftrightarrow a=b+5\)(2)
Thay (2) vào (1), ta được:
\(b^2-16\left(b+5\right)=0\)
\(\Leftrightarrow b^2-16b+64-144=0\)
\(\Leftrightarrow\left(b-8\right)^2=144\)
\(\Leftrightarrow\left[{}\begin{matrix}b=20\\b=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=25\\a=1\end{matrix}\right.\)
Cho hàm số y = 2 x 2 + 2 m x + m - 1 có đồ thị là C m , m là tham số.
Khảo sát sự biến thiên và vẽ đồ thị hàm số khi m = -1
Với m = 1 ta được hàm số: y = 2 x 2 + 2 x
- TXĐ: D = R,
- Sự biến thiên:
+ Chiều biến thiên: y' = 4x + 2
y' = 0 ⇔ x = -1/2
+ Bảng biến thiên:
Kết luận: Hàm số nghịch biến trên (-∞; -1/2), đồng biến trên (-1/2; +∞).
Đồ thị hàm số có điểm cực tiểu là (-1/2; -1/2)
- Đồ thị:
Ta có: 2x2 + 2x = 0 ⇔ 2x(x + 1) = 0
QUẢNG CÁO⇒ x = 0; x = -1
+ Giao với Ox: (0; 0); (-1; 0)
+ Giao với Oy: (0; 0)
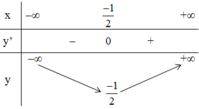
Lập bảng biến thiên và vẽ đồ thị của hàm số bậc hai
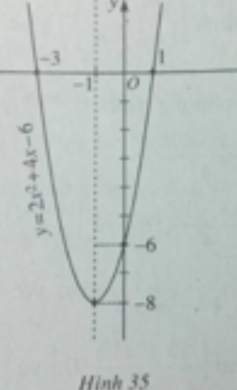
y = 2 x 2 + 4 x - 6
Hàm số bậc hai đã cho có a = 2; b = 4; c = -6;
![]()
Vì a > 0, ta có bảng biến thiên
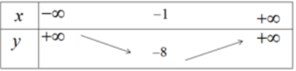
Hàm số nghịch biến trên khoảng (-∞; -1) đồng biến trên khoảng (-1; +∞)
Để vẽ đồ thị ta có trục đối xứng là đường thẳng x = -1; đỉnh I(-1;-8); giao với tục tung tại điểm (0;-6); giao với trục hoành tại các điểm (-3;0) và (1;0).
Đồ thị của hàm số y = 2 x 2 + 4 x - 6 được vẽ trên hình 35.
Khảo sát sự biến thiên và vẽ đồ thị hầm số:
a) y= x4+2x2-3
b) y= -x4-4x-1
Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số y = 4 x + 4 2 x + 1
y = 4 x + 4 2 x + 1
Tập xác định: D = R \ {−1/2}
Ta có 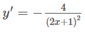
Bảng biến thiên:
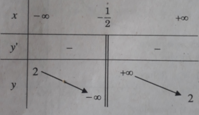
Hàm số nghịch biến trên các khoảng (− ∞ ; −1/2) và (−1/2; + ∞ )
Tiệm cận đứng: x = −1/2;
Tiệm cận ngang: y = 2.
Giao với các trục tọa độ: (0; 4) và (-1; 0)
Đồ thị:
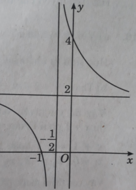
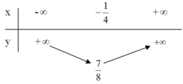
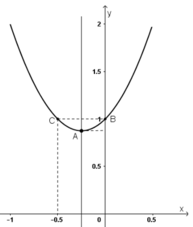
Lập bảng biến thiên và vẽ đồ thị của các hàm số: y = 2x2 + x + 1
y = 2x2 + x + 1
+ Tập xác định: R
+ Đỉnh A(–1/4 ; 7/8).
+ Trục đối xứng x = –1/4.
+ Đồ thị không giao với trục hoành.
+ Giao điểm với trục tung B(0; 1).
Điểm đối xứng với B(0 ; 1) qua đường thẳng x = –1/4 là C(–1/2 ; 1)
+ Bảng biến thiên:
+ Đồ thị hàm số:
xét sự biến thiên và vẽ đò thị hàm số sau y=-\( \left| {2x-1} \right|\)
Cho hàm số: y = 4 x 3 + mx (m là tham số) (1)
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số ứng với m = 1.
b) Viết phương trình tiếp tuyến của (C) song song với đường thẳng y = 13x + 1.
c) Xét sự biến thiên của hàm số (1) tùy thuộc vào giá trị m.
a) y = 4 x 3 + x, y′ = 12 x 2 + 1 > 0, ∀ x ∈ R
Bảng biến thiên:
Đồ thị:
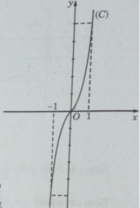
b) Giả sử tiếp điểm cần tìm có tọa độ (x0; y0) thì f′(x0) = 12 x 0 2 + 1 = 13 (vì tiếp tuyến song song với đường thẳng (d): y = 3x + 1). Từ đó ta có: x0 = 1 hoặc x0 = -1
Vậy có hai tiếp tuyến phải tìm là y = 13x + 8 hoặc y = 13x - 8
c) Vì y’ = 12 x 2 + m nên m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m ≥ 0 ta có y’ > 0 (khi m = 0; y’ = 0 tại x = 0).
Vậy hàm số (1) luôn luôn đồng biến khi m ≥ 0; y” = –6( m 2 + 5m)x + 12m
+) Với m < 0 thì y = 0 ⇔ 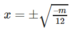
Từ đó suy ra:
y’ > 0 với

y’ < 0 với
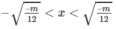
Vậy hàm số (1) đồng biến trên các khoảng
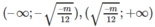
và nghịch biến trên khoảng