Trên hình 90, ta có OA = OB, ∠OAC = ∠OBD. Chứng minh:
a) ∠ODB = ∠OCA;
b) ID = IC;
c) OI là phân giác của góc DOC và OI \(\perp\) CD
Trên hình 90, ta có OA=OB, ∠OAC=∠OBD. Chứng minh:
a) ∠ODB=∠OCA;
b)ID=IC;
c) OI là phân giác của góc DOC và OI⊥CD
a: Bổ sung đề: OD=OC
XétΔODB và ΔOCA có
OD=OC
góc O chung
OB=OA
Do đó: ΔODB=ΔOCA
b: Xét ΔIAD và ΔIBC có
góc IAD=góc IBC
AD=BC
góc IDA=góc ICB
Do đó: ΔIAD=ΔIBC
=>ID=IC và IA=IB
c: Xet ΔOID và ΔOIC có
OI chung
ID=IC
OD=OC
Do đó: ΔOID=ΔOIC
=>góc DOI=góc COI
=>OI là phân giác của góc COD
OD=OC
ID=IC
Do đó: OI là trung trực của CD
=>OI vuông góc với CD
Trên hình 100 ta có OA = OB, góc OAC = góc OBD. Chứng minh rằng AC = BD
Xét ΔOAC và ΔOBD có:
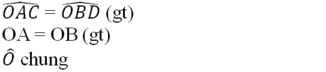
Nên ΔOAC = ΔOBD (g.c.g)
Suy ra AC = BD (hai cạnh tương ứng).
(Cho góc xoy nhỏ hơn 90 độ. Trên tia ox lần lượt lấy điểm A và D(OA<OD). Trên tia oy lần lượt lấy B và C sao cho oa= OB, Góc OAC khác OBD. Chứng minh rằng AC= BD
Trên hình 100 ta có \(OA=OB;\widehat{OAC}=\widehat{OBD}\)
Chứng minh rằng AC = BD ?
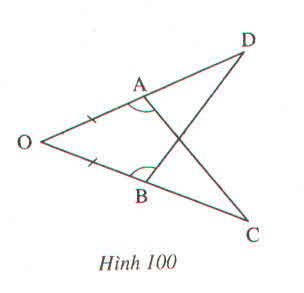
Xét tam giác OAC và tam giác OBD có:
góc OAC= góc OBD (gt)
OA=OB (gt)
góc O là góc chung
Do đó: tam giác OAC = tam giác OBD(g.c.g)
=> AC=BD
Vậy AC=BD
Trên hình 90, ta có OA=OB, OAC=OBD.Chứng minh AC=BD.
Sao thấy bạn nói "trên hình 90" mà hổng thấy hình đâu?
Bài 2: Cho góc xOy khác góc bẹt. Lấy các điểm A,B thuộc tia Ox sao cho
OA< OB, lấy C,D thuộc Oy sao cho OA = OD, OB=OC. Gọi E là giao điểm của AC và BD. Chứng minh rằng:
a) Chứng minh △ OAC =
△ODB
b) chứng minh AC =BD
Bài 3:Cho tam giác ABC , trên tia đối của tia CB lấy điểm D sao cho CB = CD . Kẻ đường thẳng qua D song song với AB và cắt tia AC tại M.
a) Chứng minh △ ABC =
△MDC
b) Chứng minh C là trung điểm của AM
a: Xét ΔOAC và ΔODB có
OA=OD
\(\widehat{O}\) chung
OC=OB
Do đó: ΔOAC=ΔODB
Cho góc nhọn xOy. Trên tia Ox lấy điểm A, trên Oy lấy điểm B sao cho OA=OB. Trên tia Ax lấy điểm D, trên tia By lấy điểm C sao cho AD=BC.
a, Chứng minh ΔAOC=ΔBOD và \(\widehat{OAC}\)=\(\widehat{OBD}\)
b, Gọi N lầ giao điểm của AC và BD. Chứng minh ΔADN=ΔBCN và ON là phân giác của \(\widehat{xOy}\)
c, Gọi H,K lần lượt là giao điểm của ON với DC và AB. Chứng minh OH⊥CD, AB//CD.
cho góc nhọn xOy. trên tia Ox lấy các đoạn OA=4,OB=8. trên tia OY lấy các đoạn OC=2, OD=4.
a) chứng minh tam giác OAC đồng dạng với tam, giác OBD.
b) gọi I là giao điểm của AD và BC. chứng minh: IA.ID=IB.IC
Cho \(\widehat{xOy}\)khác góc bẹt, trên tia Ox lấy 2 điểm A, D (A nằm giữa O, D), trên tia Oy lấy 2 điểm B, C (B nằm giữa O, D) sao cho OA =OB, \(\widehat{OAC}=\widehat{OBD}\)
a) Chứng minh \(\Delta OAC=\Delta OBD\)
b) Chứng minh \(\Delta ADC=\Delta BCD\)
c) Gọi I là giao điểm của AC và BD. Chứng minh \(\Delta OIA=\Delta OID\)
Cho góc nhọn xÔy. Trên tia ox lấy điểm B, trên tia Oy lấy điểm A sao cho OA=OB. Vẽ tia phân giác của xÔy, Trên tia Oz lấy điểm C
a) chứng minh rằng: tam giác OBC= tam giác OAC
b) chứng minh rằng: góc OCB = góc OCA và CB= CA