Mọi người giúp với ạ :( . Tìm lim
Un = 2/(Un - 1) + 1 ; U0 = 1.
Cho dãy số u n được xác định bởi u 1 = 1 ; u n + 1 = 1 2 u n + 2 u n với mọi n ≥ 1 . Tìm lim u n
A. 1
B. -1
C. 2
D. - 2
Cho dãy số (Un) xác định bởi: {U1=2; Un+1= 2Un + 3.2^n+1;∀n ϵ N*
Tính lim Un/(2n + 1).2^n-1
Ai đó giải bài tập giúp em với ạ, em cảm ơn rất nhiều
Biết dãy số u n thỏa mãn u n - 1 < 1 3 với mọi n. Chứng minh rằng: l i m u n = 1 .
Đặt vn = un – 1.
Lấy số dương d > 0 bé tùy ý
⇒ luôn tồn tại 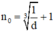 thỏa mãn
thỏa mãn 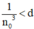
⇒ 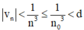 với mọi n ≥ n0.
với mọi n ≥ n0.
⇒ Theo định nghĩa ta có:
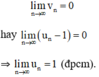
cho dãy số (un) thỏa mãn lim(un-2)=0 với mọi n thuộc N*. giá trị lim(un2+2un-1) bằng?
help pls
\(\lim\left(u_n-2\right)=0\) ;\(\forall n\Rightarrow\lim\left(u_n\right)=2\)
\(\Rightarrow\lim\left(u_n^2+2u_n-1\right)=2^2+2.2-1=7\)
Cho dãy số Un xác định bởi: \(\left\{{}\begin{matrix}u_1=\dfrac{1}{4}\\u_{n+1}=u_n^2+\dfrac{u_n}{2}\end{matrix}\right.\) với mọi \(n\ge1\). Tìm lim Un
Cho hai dãy số ( u n ) và ( v n ) . Chứng minh rằng nếu lim v n = 0 v à | u n | ≥ v n với mọi n thì l i m u n = 0
l i m v n = 0 ⇒ | v n | có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi (1)
Vì | u n | ≤ v n v à v n ≤ | v n | với mọi n, nên | u n | ≤ | v n | với mọi n. (2)
Từ (1) và (2) suy ra | u n | cũng có thể nhỏ hơn một số dương bé tuỳ ý, kể từ một số hạng nào đó trở đi, nghĩa là l i m u n = 0
Cho dãy số u n với u n = n + 1 n + 2 . Khi đó, lim u n = ?
A. 1 2
B. 2 2
C. 0
D. + ∞
Tìm lim un với un=\(\sum\limits^n_{k=1}sin^k\alpha\) (α≠\(\dfrac{\pi}{2}\) +kπ, k ϵ Z)
Cho dãy số ( u n ) với u n = 1 + 2 + 3 + 4 + . . . + n ( 1 + 3 + 3 2 + 3 3 + . . . + 3 n ) . n + 1 . Tính l i m u n
A. 0
B. 2
C. 1 3
D. 1
* Xét tử số: Ta thấy 1, 2, 3, 4, ..., n là một dãy số thuộc cấp số cộng có n số hạng với
u 1 = 1 ; d= 1 .
Tổng n số hạng của cấp số cộng: S n = u 1 + u n n 2 = 1 + n n 2 .
* Xét mẫu số: Ta thấy 1 , 3 , 3 2 , 3 3 , ... , 3 n là một dãy số thuộc cấp số nhân có n + 1 số hạng với u 1 = 1 ; q = 3
Tổng (n+ 1) số hạng của cấp số nhân: S n + 1 = u 1 . 1 − q n + 1 1 − q = 1 − 3 n + 1 1 − 3 = 3 n + 1 − 1 2 .
⇒ u n = n 3 n + 1 − 1 = n 3.3 n − 1
Bằng quy nạp ta luôn có n < 2 n , ∀ n ∈ ℕ * và 3 n > 1 , ∀ n ∈ ℕ *
⇒ u n = n 3.3 n − 1 < n 3 n < 2 n 3 n = 2 3 n
Vì lim 2 3 n = 0 nên lim u n = 0.
Chọn đáp án A