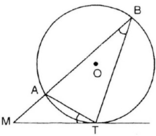
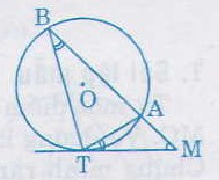
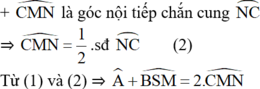Bài 2: Qua điểm M nằm bên ngoài ( ); R) Kẻ 2 tiếp tuyến MA, MB (A, B là tiếp điểm). Vẽ cát tuyến MCD không đi qua tâm O ( C nằm giữa D)
a) CM: tứ giác MAOB nội tiếp và MO ⊥ AB
b) CM: MA . AD= MD . AC
c) Gọi I là chung điểm của dây cung CD và E là giao điểm của 2 đường thẳng AB và OI. Tính độ dài đường thẳng OE theo R khi OI = \(\dfrac{R}{3}\)
d) Qua tâm O kẻ đườn thẳng ⊥ với OM cắt các đường thẳng MA, MB lần lượt tại P, Q. Tính vị trí điểm M để diện tích tam giác MPQ đạt giá trị nhỏ nhất
(mink đag cần gấp)