Cho tam giác MOA vuông tại M, đường cao MH. Biết MO = 5 cm; MA = 7cm.Tính OH, HA, MH.
9L
Những câu hỏi liên quan
Câu 8. Cho tam giác MNP vuông tại M, đường cao MH, phân giác MD. Biết MN = 18 cm, MO = 24 cm. Độ dài NH, MH, HD là Gấp !!!
Sửa đề: MP=24cm
NP=căn 18^2+24^2=30cm
NH=MN^2/NP=18^2/30=324/30=10,8cm
MH=18*24/30=14,4cm
Đúng 0
Bình luận (0)
Cho tam giác MNP vuông tại M, đường cao MH. Biết NH = 5 cm, HP = 9 cm. Độ dài MH bằng:
Cho tam giác MNP vuông tại M đường cao MH. Biết NH = 1,8 cm; MH = 2,4cm. Tính diện tích của ∆MNP
Áp dụng hệ thức lượng trong tam giác vuông vào ΔNMP vuông tại M có MH là đường cao ứng với cạnh huyền NP, ta được:
\(MH^2=HN\cdot HP\)
\(\Leftrightarrow HP=\dfrac{2.4^2}{1.8}=3.2\left(cm\right)\)
Diện tích tam giác MNP là:
\(S_{MNP}=\dfrac{MH\cdot NP}{2}=\dfrac{2.4\cdot5}{2}=6\left(cm^2\right)\)
Đúng 2
Bình luận (0)
Áp dụng hệ thức trong tam giác vuông:
`MH^2 =NH.PH`
`=>PH=MH^2 : NH = 2,4^2 : 1,8=3,2(cm)`
`=> NP=NH+PH=5(cm)`
`=> S= 1/2 . MH .NP =6(cm^2)`
Đúng 1
Bình luận (0)
cho tam giác MNP vuông tại M đường cao MH đường ME là tia phân giác của góc M biết NE = 4,5 cm EP = 6 cm Tính diện tích tam giác MHE
Xem chi tiết
\(NP=4,5+6=10,5\left(cm\right)\)
Áp dụng tích chất đường phân giác:
\(\frac{MN}{NE}=\frac{MP}{EP}\Leftrightarrow\frac{MN}{4,5}=\frac{MP}{6}\Leftrightarrow MN=\frac{3}{4}MP\).
Áp dụng định lí Pythagore:
\(NP^2=MP^2+MN^2\)
\(\Leftrightarrow10,5^2=MP^2+\left(\frac{3}{4}MP\right)^2\Leftrightarrow MP=8,4\Rightarrow MN=6,3\)
\(MH=\frac{MN.MP}{NP}=\frac{8,4.6,3}{10,5}=5,04\)
\(NH=\frac{MN^2}{NP}=\frac{6,3^2}{10,5}=3,78\)
\(HE=NE-NH=4,5-3,78=0,72\)
\(S_{MHE}=\frac{1}{2}.MH.HE=\frac{1}{2}.0,72.5,04=1,8144\left(cm^2\right)\)
Câu 10. Cho tam giác MNP vuông tại M, đường cao MH, phân giác MD. Biết MN = 72 cm, MP = 96 cm. Độ dài NH, MH, HD là
Gấp !!!
(Tự vẽ hình)
- Xét △MNP vuông tại M, áp dụng định lí Pytago:
\(^{NM^2}\)+\(MP^2\)=\(NP^2\)
=\(72^2\)+\(96^2\)=\(NP^2\)
⇔\(NP^2\)=\(72^2\)+\(96^2\)=14400
⇔\(NP\)=\(\sqrt{14400}\)=120cm
- Xét △MNP vuông tại M, đường cao MH, theo hệ thức lượng ta có:
\(MN^2\)=\(NH.NP\)
\(72^2\)=\(NH.120\)
⇔\(NH\)=\(\dfrac{72^2}{120}\)=43,2 cm
- \(MH.NP\)=\(MP.MN\)
⇔ \(MH\)=\(\dfrac{MP.MN}{NP}\)=\(\dfrac{96.72}{120}\)=3,6cm
Đúng 0
Bình luận (0)
Câu 9:
Cho tam giác MNP vuông tại M, đường cao MH. Biết MH = 12cm và . Khi đó MP =.... cm. Câu 10:
. Khi đó MP =.... cm. Câu 10:
Cho tam giác MNP vuông tại M, đường cao MH. Biết MH = 12cm và . Khi đó NP =.... cm.
. Khi đó NP =.... cm.
Xem chi tiết
Cho tam giác MNP vuông tại M, đường cao MH. Biết MH = 12cm và
Cho tam giác MNP vuông tại M, đường cao MH. Biết MH = 12cm và
ta sử dụng hệ thức lượng trong tam giác vuông
\(\frac{1}{MN^2}+\frac{1}{MP^2}=\frac{1}{AH^2}\)
mà MN=3MP/4
they vào ta đc : \(\frac{1}{\left(\frac{3}{4}MP\right)^2}+\frac{1}{MP^2}=\frac{1}{12^2}\)
<=> \(\frac{16}{9MP^2}+\frac{1}{MP^2}=\frac{1}{12^2}\)
<==> \(\frac{25}{9MP^2}=\frac{1}{12^2}\)=>\(MP^2=\frac{12^2.15}{9}=240\)
=> MP=\(4\sqrt{15}\)
bài 10: gống cái trên :
tiếp : tính:\(NM=\frac{3}{4}MP=3\sqrt{15}\)
áp dungnj đl pita go ta có :
NP=\(\sqrt{MN^2+MP^2}=5\sqrt{15}\)
Đúng 0
Bình luận (0)
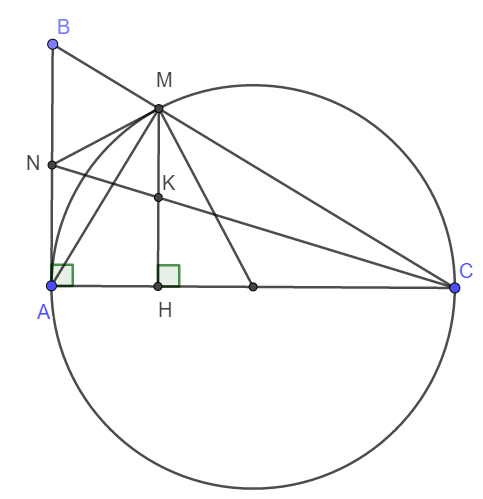
Cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AC cắt BC tại M
a. CM tam giác AMC VUÔNG
B. TIẾT TIẾP TẠI M CỦA (O) CẮT AB TẠI N. CM AN=NB
C. ĐƯỜNG CAO MH CỦA TAM GIÁC AMC CẮT NC TẠI K. CM K LÀ TRUNG ĐIỂM MH
- # Bn có thể gửi từng câu đc ko ? Gửi từng câu thì các bn khác sẽ dễ dàng trl hơn :)
Đúng 0
Bình luận (0)
a) Ta thấy ngay \(\widehat{AMC}\) là góc nội tiếp chắn nửa đường tròn nên \(\widehat{AMC}=90^o\)
hay tam giác AMC vuông.
b) Ta thấy NA cũng là tiếp tuyến của (O) tại A.
Áp dụng tính chất hai tiếp tuyến cắt nhau, ta có NM = NA.
Xét tam giác vuông ABM có NM = NA nên \(\widehat{NAM}=\widehat{NMA}\Rightarrow\widehat{NBM}=\widehat{NMB}\) (Cùng phụ với hai góc trên)
\(\Rightarrow NM=NB\)
Vậy nên NA = NB.
c) Ta thấy ngay MH // AB nên áp dụng định lý Ta let ta có:
\(\frac{KH}{NA}=\frac{KC}{KN}=\frac{MK}{NB}\)
Lại có NA = NB nên KH = MK hay K là trung điểm MH.
Đúng 0
Bình luận (0)
1) cho tam giác ABC vuông tại A. Đường tròn tâm O đường kính AC cắt BC tại M
a. CM tam giác AMC VUÔNG
B. TIẾT TIẾP TẠI M CỦA (O) CẮT AB TẠI N. CM AN=NB
C. ĐƯỜNG CAO MH CỦA TAM GIÁC AMC CẮT NC TẠI K. CM K LÀ TRUNG ĐIỂM MH
cho tam giác MNP vuông tại M có MH là đường cao biết NP=5cm NH=1.8 cm Tính độ dài MN MH và tính góc N và P b, qua P vẽ đường cao song song với MN cắt MH tại D chứng minh MH . MD = PH . PN
b: Xét ΔPDM vuông tại P có PH là đường cao ứng với cạnh huyền MD, ta được:
\(MH\cdot MD=MP^2\left(1\right)\)
Xét ΔMNP vuông tại M có MH là đường cao ứng với cạnh huyền NP, ta được:
\(PH\cdot PN=MP^2\left(2\right)\)
Từ (1) và (2) suy ra \(MH\cdot MD=PH\cdot PN\)
Đúng 0
Bình luận (0)





