Cho tam giác ABC, trung tuyến AE, CD. Gọi N là điểm đối xứng với B qua E; M là điểm đối xứng với C qua D.
a) C/m: tứ giác AMBC là hình bình hành.
b) M và N đối xứng qua A
c) DE = MN/4
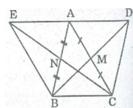
Cho tam giác ABC vuông tại A. AE là đường trung tuyến. Gọi M là điểm đối xứng của E qua AB, I là giao điểm của AB và ME, N đối xứng E qua AC, K là giao điểm AC và NE. a) Chứng minh AE = IK b) Chứng minh M đối xứng N qua A. Vậy thôi ạ, giúp mình với, mai mình thi học kỳ rồi :(
a: E đối xứng M qua AB
nên AB là trung trực của ME
=>AB vuông góc với ME tại trung điểm của ME
=>AB là phân giác của góc EAM(1)
E đối xứng N qua AC
nên AC là trung trực của NE
=>AC vuông góc với NE tại trung điểm của NE
=>AC là phân giác của góc EAN(2)
Xét tứ giác AIEK có
góc AIE=góc AKE=góc KAI=90 độ
nên AIEK làhình chữ nhật
b: Từ (1), (2) suy ra góc NAM=2*90=180 độ
=>N,A,M thẳng hàng
mà AM=AN
nên A là trung điểm của MN
Cho tam giác ABC cân tại A có trung tuyến BM. Gọi D là điểm đối xứng với B qua M.
a) Tứ giác ABCD là hình gì? Vì sao?.
b) Qua D kẻ đường thẳng song song với AC cắt đường thẳng BC tại E. Gọi O là giao điểm của AE và CD. Gọi N là giao điểm của MO và DE. Chứng minh BE = 2MN.
c) Chứng minh BE < AD + 2DE.
giúp mik vs ạ!!
a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng Với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua điểm A.
* Xét tứ giác ABCD, ta có:
MA = MC (gt)
MB = MD (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AD // BC và AD = BC (1)
* Xét tứ giác ACBE, ta có:
AN = NB (gt)
NC = NE (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)
Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE
Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.
xét tam giác ADE có:
AB=DB( gt)
AC=EC (gt)
=> BC//DE ( t/c đường trung bình)
ta có: BC//DE (CMT)
AM vuông góc với BC
AM=IM
=> góc AID= góc AIE
Xét tam giác AEI và tam giác ADIcó:
góc DAI= góc EAI
AI chung
góc AID= góc AIE (CMT)
=> tam giác AEI = tam giác ADI (g.c.g)
=> DI=EI(2 cạnh tương ứng)
Bài 11: Cho tam giác ABC, các trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M; E là điểm đối xứng với C qua N.
a) Chứng minh: tứ giác ABCD là hình bình hành;
b) Chứng minh: AE // BC;
c) Chứng minh: D và E đối xứng nhau qua A.
a: Xét tứ giác ABCD có
M là trung điểm của AC
M là trung điểm của BD
Do đó: ABCD là hình bình hành
a. Vì tam giác ABC có trung tuyến BM (gt)
-> M là trung điểm AC
Vì D đối xứng với B qua M (gt)
-> M là trung điểm BD
xét tứ giác ABCD có : - M là trung điểm AC (cmt)
- M là trung điểm BD (cmt)
=> tứ giác ABCD là hình bình hành
b) Vì tam giác ABC có trung tuyến CN(gt)
-> N là trung điểm AB
Vì E đối xứng với C qua N (gt)
-> N là trung điểm EC
xét tứ giác AEBC có : - N là trung điểm AB (cmt)
- N là trung điểm EC (cmt)
-> tứ giác AEBC là hình bình hành
=> AE // BC ( tính chất )
c)Vì tứ giác ABCD là hình bình hành ( cmt )
-> AD = BC (tính chất) (1)
Vì tứ giác AEBC là hình bình hành ( cmt )
-> AE = BC (2)
từ (1) và (2) => AE = AD
=> A là trung điểm ED
=> E đối xứng vói D qua A
Bài 2: Cho tam giác ABC có trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm
đối xứng với C qua N. CMR: D đối xứng với E qua A.
* Xét tứ giác ABCD, ta có:
MA = MC (gt)
MB = MD (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ABCD là hình bình hành (vì có hai đường chéo cắt nhau tại trung điểm của mỗi đường)
⇒ AD // BC và AD = BC (1)
* Xét tứ giác ACBE, ta có:
AN = NB (gt)
NC = NE (định nghĩa đối xứng tâm)
Suy ra: Tứ giác ACBE là hình bình hành (vì có 2 đường chéo cắt nhau tại trung điểm của mỗi đường) ⇒ AE // BC và AE = BC (2)
Từ (1) và (2) suy ra: A, D, E thẳng hàng và AD = AE
Nên A là trung điểm của DE hay điểm D đối xứng với điểm E qua điểm A.
Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua
M, gọi E là điểm đối xứng Với C qua N. Chứng minh rằng điểm D đối xứng với điểm E qua
điểm A.
Xét tứ giác ABCD có
AM=CM; BM=DM => ABCD là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AD//=BC
Xét ứ giác ACBE có
AN=BN; CN=EN => ACBE là hình bình hành (tứ giác có 2 đường chéo cắt nhau tại trung điểm mỗi đường là hbh)
=> AE//=BC
=> AD=AE =BC
=> AE trùng AD hay A; D; E thẳng hàng (Qua 1 điểm ngoài đường thẳng chỉ dựng được duy nhất 1 đường thẳng // với đường thẳng đã cho)
=> D đối xứng với E qua A
Cho tam giác ABC vuông tại A, trung tuyến AM. Gọi I là trung điểm của AB; N là điểm đối xứng với M qua I, E là điểm đối xứng với M qua AC, D là điểm đối xứng với A qua M.
Chứng minh điểm E đối xứng với điểm N qua A.
Tam giác ABC cần thêm điều kiện gì thì tứ giác AECB là hình thang cân.
cho tam giác ABC , các đường trung tuyến BN, CM gọi D là điểm đối xứng với B qua N , gọi E là điểm đối xứng C qua M
a) chứng minh các tứ giác ABCD, AEBC là hình bình hành
b) chứng minh E đối xứng với D qua A
a, Vì N là trung điểm BD và AC nên ABCD là hbh
Vì M là trung điểm CE và AB nên AEBC là hbh
b, Vì ABCD và AEBC là hbh nên \(\left\{{}\begin{matrix}AE//BC;AE=BC\\AD//BC;AD=BC\end{matrix}\right.\Rightarrow AE\equiv AD;AE=AD\)
Vậy E đx D qua A
Cho tam giác ABC, các đường trung tuyến BM, CN. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với C qua N.
Chứng minh rằng điểm D đối xứng với điểm E qua điểm A ?