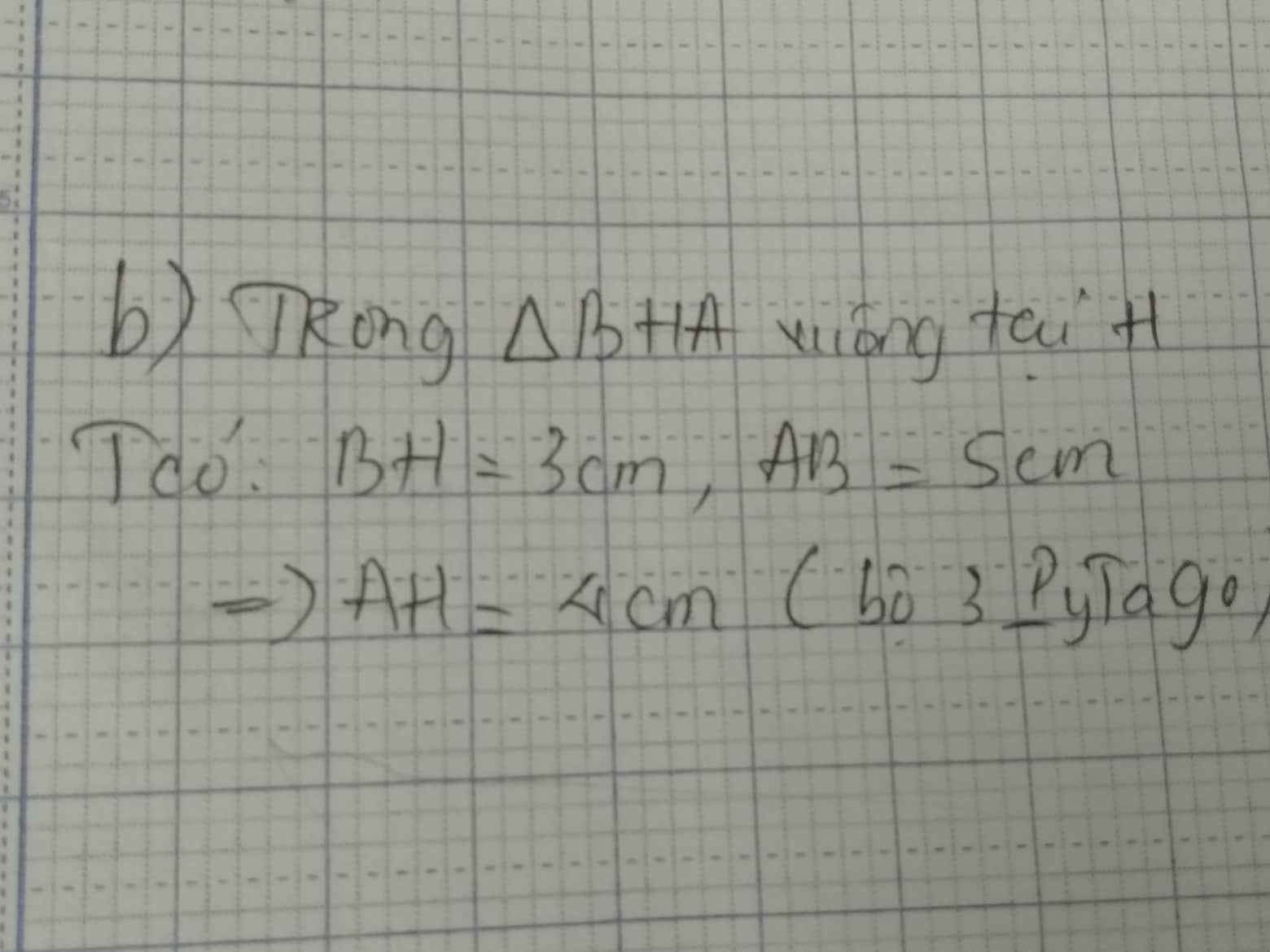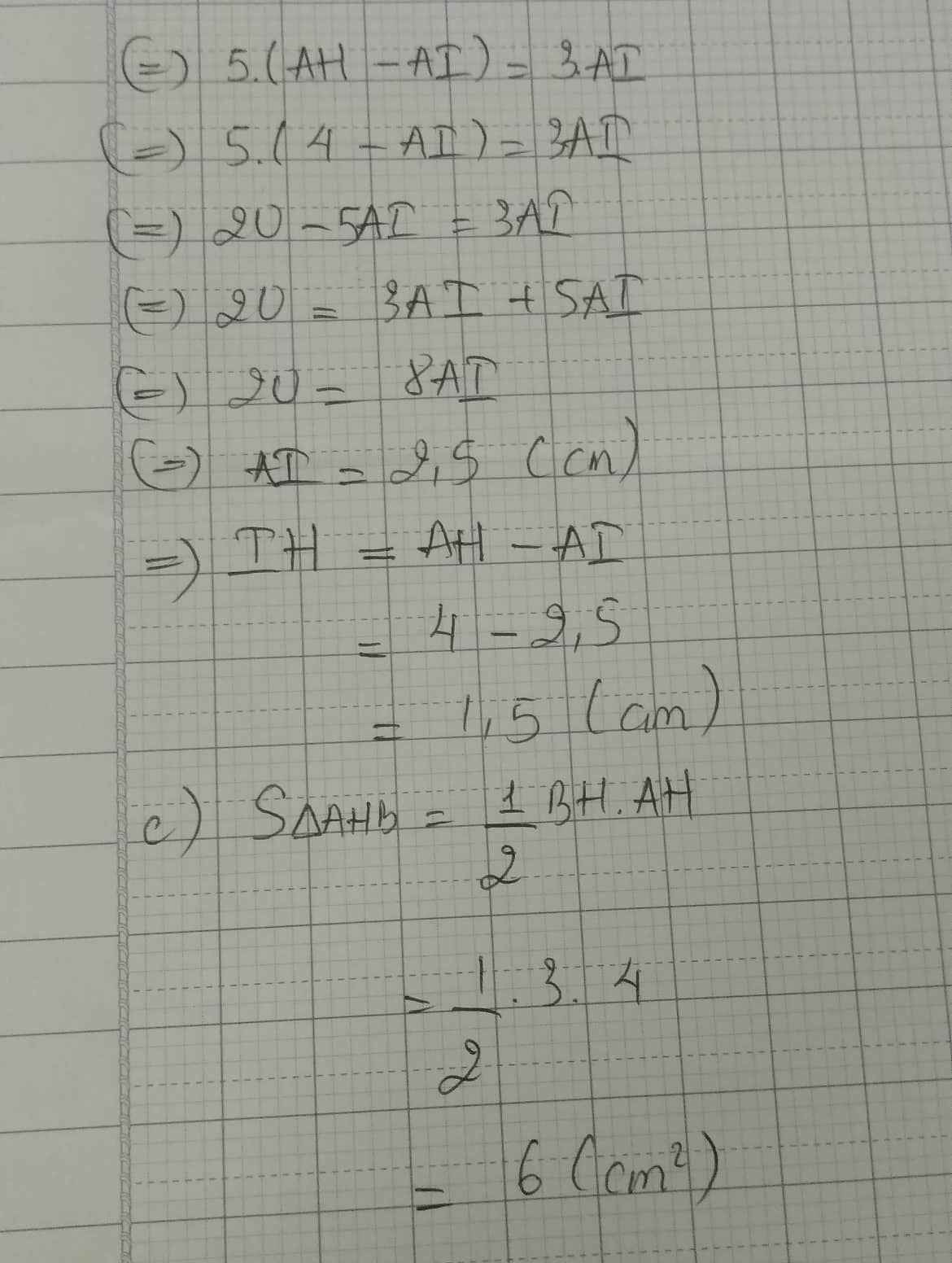tam giác ABC, I;O lần lượt là tâm dường tròn nội tiếp,ngoại tiếp tam giác; G là trọng trong tâm. CMR: Nếu goc AIO=90 độ thì IG // BC
KA
Những câu hỏi liên quan
Tam giác ABC có ba đường phân giác cắt nhau tại I. Biết rằng I cũng là giao điểm ba đường trung trực của tam giác ABC. Chứng minh tam giác ABC đều.
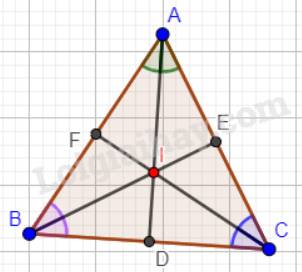
Ta có: I là giao điểm của ba đường phân giác của tam giác ABC. Đồng thời là giao điểm của ba đường trung trực tam giác ABC nên: \(ID \bot BC;IE \bot AC;IF \bot AB\).
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\)(AD là phân giác của góc A);
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\)(vì \(ID \bot BC\)).
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC ( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta BEA = \Delta BEC\)(g.c.g). Suy ra: BA = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều.
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH
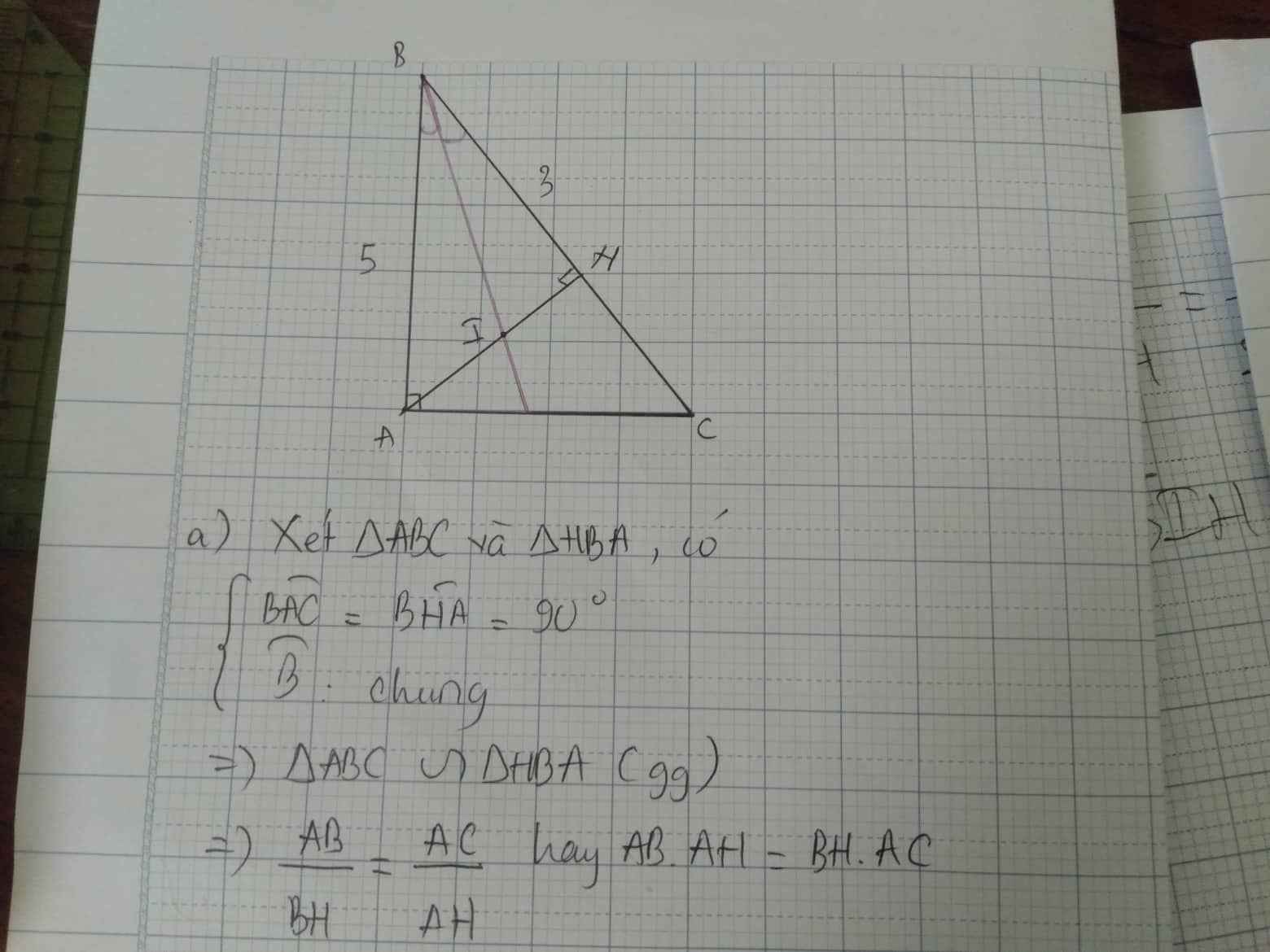
a) CM: tam giác ABC đồng dạng tam giác HBA, từ đó suy ra: AB.AH = BH.AC
b) Tia phân giác góc ABC cắt AC tại I (i). Biết AB=9cm; AC=12cm. Tính AI (ai), BC
c) Tính tỉ số diện tích tam giác HAB và tam giác HCA
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng với ΔHBA
=>AB/HB=AC/HA
=>AB*HA=HB*AC
b: BC=căn 9^2+12^2=15cm
BI là phân giác
=>AI/AB=CI/BC
=>AI/3=CI/5=12/8=1,5
=>AI=4,5cm
c: S HAB/S HCA=(AB/CA)^2
Đúng 0
Bình luận (0)
Bài 1: Cho hình tam giác ABC . Trên cạnh BC lấy K sao cho : KB = KC
a) So sánh diện tích tam giác ABK với diện tích tam giác AKC .
b ) Diện tích tam giác ABC gấp mấy lần diện tích tam giác ABK ?
c ) Biết diện tích tam giác ABC = 48cm2 ; AM = 1/3 AK . Tính diện tích tam giác AMC
( Làm nhanh dc tick
Câu 11: Cho tam giác ABC, gọi E, F, I lâm lượt là trung điểm của AB, AC, BC.
Tam giác ABC cần điều kiện gì thì tứ giác AFIE là hình thoi.
A. Tam giác ABC cân tại A.
C.Tam giác ABC vuông tại A
B. Tam giác ABC cân tại C
D. Tam giác ABC cân tại B.
Cho tam giác ABC vuông tại A, đường cao AH
a) CM: tam giác ABC đồng dạng tam giác HBA, từ đó suy ra: AB.AH = BH.AC
b) Tia phân giác góc ABC cắt AH tại I (i). Biết BH=3cm; AB=5cm. Tính AI (ai), IH (ih)
c) Tính diện tích tam giác AHB
cho tam giác ABC (ABAC). AM lcho tam giác ABC (ABAC). AM là tia phân giác của góc BAC ( M thuộc BC) lấy I lấy I là trung điểcho tam giác ABC (ABAC). AM là tia phân giác của góc BAC ( M thuộc BC) lấy I lấy I là trung điểm của AB trên MI lấy K sao cho N là trung điểm của MC trên tia AN lấy E sao cho tam giác N NEm của AB trên MI lấy K sao cho N là trung điểm của MC trên tia AN lấy E sao cho tam giác N NEà tia phân giác của góc BAC ( M thuộc BC) lấy I lấy I là trung điểm của AB trên MI lấy K sao...
Đọc tiếp
cho tam giác ABC (AB=AC). AM lcho tam giác ABC (AB=AC). AM là tia phân giác của góc BAC ( M thuộc BC) lấy I lấy I là trung điểcho tam giác ABC (AB=AC). AM là tia phân giác của góc BAC ( M thuộc BC) lấy I lấy I là trung điểm của AB trên MI lấy K sao cho N là trung điểm của MC trên tia AN lấy E sao cho tam giác N = NEm của AB trên MI lấy K sao cho N là trung điểm của MC trên tia AN lấy E sao cho tam giác N = NEà tia phân giác của góc BAC ( M thuộc BC) lấy I lấy I là trung điểm của AB trên MI lấy K sao cho N là trung đicho tam giác ABC (AB=AC). AM là tia phân giác của góc BAC ( M thuộc BC) lấy I lấy I là trung điểm của AB trên MI lấy K sao cho N là trung điểm của MC trên tia AN lấy E sao cho tam giác N = NEểm của MC trên tia AN lấy E sao cho tam giác N = NE
Đề bài yêu cầu chứng minh gì vậy bạn?
Đúng 0
Bình luận (0)
Quinn ko hiểu
đề bài ko có yêu cầu???![]()
Đúng 0
Bình luận (0)
Cho tam giác ABC. Gọi AD là đường phân giác của tam giác ABC, I là giao điểm của 3 đường phân giác của tam giác và H là hình chiếu của I trên cạnh BC. Chứng minh: BIH = CID
Lời giải:
Ta thấy:
$\widehat{BID}=180^0-\widehat{BIA}=\widehat{ABI}+\widehat{BAI}$
$=\frac{\widehat{B}}{2}+\frac{\widehat{A}}{2}=\frac{\widehat{A}+\widehat{B}}{2}$
$=\frac{180^0-\widehat{C}}{2}=90^0-\widehat{C}.\frac{1}{2}$
$=90^0-\widehat{ICH}=\widehat{CIH}$
Vậy:
$\widehat{BID}=\widehat{CIH}$
$\Rightarrow \widehat{BIH}+\widehat{HID}=\widehat{HID}+\widehat{CID}$
$\Rightarrow \widehat{BIH}=\widehat{CID}$ (đpcm)
Đúng 2
Bình luận (0)
cho tam giác ABC vuông tại B có góc A=50 độ, lấy điểm D trên tia AB.Sao cho AD=AC, từ D kẻ DE vuông góc AC tại E.a,chứng minh tam giác ABC=tam giác AED . b,chứng minh tam giác ABC là tam giác cân c, gọi I là trung điểm của BE . CMR A,I,M thẳng hàng
cho tam giác ABC vuông tại A . E là trung điểm của BC . I là tâm đường tròn nội tiếp tam giác ABC , tam giác IEC vuông . Tính tỉ số giữa các cạnh tam giác ABC
Cho tam giác ABC, tia phân giác góc BAC cắt tia phân giác góc ngoài tại C của tam giác ABC tại I. Chứng minh ABC=2AIC Gợi ý: Sử dụng tính chất góc ngoài tại đỉnh C của tam giác ABC và giác ngoài tại đỉnh C của tam giác AIC