Cho tam giác ABC. Trên BC, CA, AB lần lượt lấy các đoạn thẳng BA’ = 2CB ; CB’ = 2CA ; AC’ = 2AB. Tính tỉ số\(\dfrac{S}{S'}\) ( Với S là diện tích của tam giác ABC, là diện tích của tam giác A’B’C’)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
NG
Những câu hỏi liên quan
Cho tam giác ABC trên tia đối của tia BA, CA lần lượt lấy các điểmP, Q sao cho BP = CQ. Gọi M, N lần lượt là trung điểm của các đoạn thẳng BC, PQ. Đường thẳng MN cắt các đường thẳng AB và AC thứ tự tại I và K. Chứng minh rằng tam giác AIK cân.
Cho tam giác ABC trên tia đối của BA,CA lần lượt lấy các điểm P,U sao cho BP=CU gọi M,N lần lượt là trung điểm của các đoạn thảng BC và PU đường thẳng MN cắt các đường thảng AB và AC tại I và K .CM tam giác AIK cân
Trên tia đối của tia MP lấy D sao cho M là trung điểm của PD
Xét tứ giác BPCD có
M là trung điểm chung của BC và PD
nên BPCD là hình bình hành
=>BP=CD và BP//CD
mà BP=CQ(GT)
nên CD=CQ
=>\(\widehat{CDQ}=\widehat{CQD}=\dfrac{180^0-\widehat{QCD}}{2}\)
BP//CD
=>AB//CD
=>\(\widehat{DCQ}=\widehat{IAK}\)
Xét ΔPDQ có
M,N lần lượt là trung điểm của PD,PQ
=>MN là đường trung bình
=>MN//DQ
=>IK//DQ
=>\(\widehat{CQD}=\widehat{AKI}\)
=>\(\widehat{AKI}=\widehat{AIK}\)
=>ΔAKI cân tại A
Đúng 0
Bình luận (0)
Tam giác ABC đều Trên các cạnh AB, BC,CA lần lượt lấy 3 điểm M,N,P sao cho AM=BN=CP Ba đoạn thẳng
NA,BP,CM cắt nhau tại D,E,F Chứng minh tam giác DEF đều
Tam giác ABC đều Trên các cạnh AB, BC,CA lần lượt lấy 3 điểm M,N,P sao cho AM=BN=CP Ba đoạn thẳng
NA,BP,CM cắt nhau tại D,E,F Chứng minh tam giác DEF đều
1. Cho tam giác ABC. Trên tia đối của BA, CA lần lượt lấy các điểm P,Q sao cho BPCQ. Gọi M,N lần lượt là các trung điểm của ác đoạn BC, PQ. Đường thẳng MN cắt đường thẳng AB, AC lần lượt tại I,K. CMR: tam giác AIK cân2. Cho tam giác ABC, AM là trung tuyến. Vẽ đường thẳng d đi qua trung điểm I của AM và cắt AB,AC. Gọi A,B,C là hình chiếu của A,B,C trên đường thẳng d. CMR: AA (BB+CC)/2
Đọc tiếp
1. Cho tam giác ABC. Trên tia đối của BA, CA lần lượt lấy các điểm P,Q sao cho BP=CQ. Gọi M,N lần lượt là các trung điểm của ác đoạn BC, PQ. Đường thẳng MN cắt đường thẳng AB, AC lần lượt tại I,K. CMR: tam giác AIK cân
2. Cho tam giác ABC, AM là trung tuyến. Vẽ đường thẳng d đi qua trung điểm I của AM và cắt AB,AC. Gọi A',B',C' là hình chiếu của A,B,C trên đường thẳng d. CMR: AA'= (BB'+CC')/2
Trên tia đối của MP lấy điểm D sao cho MP=MD.
Ta có: \(\Delta\)MBP=\(\Delta\)MCD (c.g.c) => BP=CD (2 cạnh tương ứng)
Mà BP=CQ => CD=CQ => \(\Delta\)DCQ cân tại C => ^CQD= (1800-^DCQ)/2
=> ^MPB=^MDC (2 góc tương ứng) ở vị trí so le trong => AB//CD => ^DCQ=^IAK (Đồng vị)
M là trung điểm PD, N là trung điểm PQ => MN là đường trung bình của \(\Delta\)PDQ
=> MN//DQ hay IK//DQ => ^CQD=^AKI (Đồng vị)
=> \(\Delta\)AIK có: ^AKI= (1800-^IAK)/2 = (1800-^DCQ)/2 = ^CQD
=> Tam giác AIK cân tại A (đpcm)
Đúng 1
Bình luận (0)
I. Nội qui tham gia "Giúp tôi giải toán"
1. Không đưa câu hỏi linh tinh lên diễn đàn, chỉ đưa các bài mà mình không giải được hoặc các câu hỏi hay lên diễn đàn;
2. Không trả lời linh tinh, không phù hợp với nội dung câu hỏi trên diễn đàn.
3. Không "Đúng" vào các câu trả lời linh tinh nhằm gian lận điểm hỏi đáp.
Các bạn vi phạm 3 điều trên sẽ bị giáo viên của Online Math trừ hết điểm hỏi đáp, có thể bị khóa tài khoản hoặc bị cấm vĩnh viễn không đăng nhập vào trang web.
Đúng 0
Bình luận (0)
Bạn NX Toàn ơi, bạn bị rảnh ạ, rớt hết phần duyên ra rồi🙃🙃🙃
Xem thêm câu trả lời
1. Cho tam giác ABC. Trên tia đối của BA, CA lần lượt lấy các điểm P,Q sao cho BPCQ. Gọi M,N lần lượt là các trung điểm của ác đoạn BC, PQ. Đường thẳng MN cắt đường thẳng AB, AC lần lượt tại I,K. CMR: tam giác AIK cân2. Cho tam giác ABC, AM là trung tuyến. Vẽ đường thẳng d đi qua trung điểm I của AM và cắt AB,AC. Gọi A,B,C là hình chiếu của A,B,C trên đường thẳng d. CMR: AA (BB+CC)/2
Đọc tiếp
1. Cho tam giác ABC. Trên tia đối của BA, CA lần lượt lấy các điểm P,Q sao cho BP=CQ. Gọi M,N lần lượt là các trung điểm của ác đoạn BC, PQ. Đường thẳng MN cắt đường thẳng AB, AC lần lượt tại I,K. CMR: tam giác AIK cân
2. Cho tam giác ABC, AM là trung tuyến. Vẽ đường thẳng d đi qua trung điểm I của AM và cắt AB,AC. Gọi A',B',C' là hình chiếu của A,B,C trên đường thẳng d. CMR: AA'= (BB'+CC')/2
này cái bạn nguyễn xuân toàn kia bị gì thế ? họ là hỏi bài mà !
Đúng 0
Bình luận (0)
ở câu hỏi của bạn Hồ Ngọc Thiện bạn cũng đăng nôi quy và bây giờ câu hỏi của bạn này bạn cũng cho nội quy là sao
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
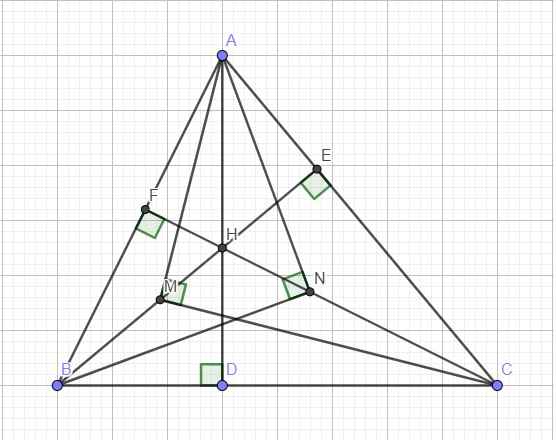
Trên mặt phẳng, cho đoạn thẳng BC=2a(a>0), lấy 1 điểm A bất kì sao cho tam giác ABC nhọn. Các đường cao AD,BR,CF cắt nhau tại H (D,E,F lần lượt nắm trên các cạnh BC, CA, AB). Trên các đoạn HB, HC lần lượt lấy M, N sao cho \(\widehat{AMC}=\widehat{BNA}=90^o\)
a) chứng minh tam giác AMN cân
b) tìm GTLN của BN.CM theo a
Tính chất cơ bản của tam giác với 3 đường cao: \(\Delta AEF\sim\Delta ABC\) (bài toán quen thuộc chắc em tự c/m được)
\(\Rightarrow AF.AB=AE.AC\)
Trong tam giác vuông ABN với đường cao NF:
\(AN^2=AF.AB\)
Trong tam giác vuông ACM:
\(AM^2=AE.AC\)
\(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\)
b. Hệ thức lượng: \(BN^2=BF.AB\) ; \(CM^2=CE.AC\)
\(\Delta ABD\sim\Delta CBF\) (2 tam giác vuông chung góc B)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BD}{BF}\Rightarrow BF.AB=BD.BC\) (1)
Hoàn toàn tương tư, \(\Delta ADC\sim\Delta BEC\Rightarrow CE.AC=CD.BC\) (2)
Cộng vế (1) và (2) \(\Rightarrow BF.AB+CE.AC=\left(BD+CD\right)BC=BC^2\)
\(\Rightarrow BN^2+CM^2=BC^2\)
\(\Rightarrow BN.CM\le\dfrac{1}{2}\left(BN^2+CM^2\right)=\dfrac{1}{2}BC^2=2a^2\)
Dấu "=" xảy ra khi tam giác cân tại A
Đúng 2
Bình luận (1)
Cho tam giác ABC có diện tích 180 cm2. Trên các cạnh AB, BC, CA lần lượt lấy các điểm M, N, P sao cho AM = 2/3 AB, BN = 3/4 BC và CP = 1/3 CA. Tính diện tích tam giác MNP.
Cho tam giác ABC có diện tích 180 cm2. Trên các cạnh AB, BC, CA lần lượt lấy các điểm M, N, P sao cho AM = 2/3 AB, BN = 3/4 BC và CP = 1/3 CA. Tính diện tích tam giác MNP.
Xem chi tiết
Cho tui tick nha
Diện tích tam giác ABN = 1/4 diện tích tam giác ABC vì có chung chiều cao nối từ A xuống N và BN = 1/4 BC
Diện tích tam giác ABN là:
64 x 1/4 = 16 (cm2 )
Diện tích tam giác BMN = 1/2 diện tích tam giác ABN vì có chung chiều cao nối từ N xuống M và BM = 1/2 BA
Diện tích tam giác BMN là:
16 x 1/2 = 8 (cm2 )
Đáp số: 8 cm2
Đúng 1
Bình luận (0)
cô làm rồi em nhé!
https://olm.vn/cau-hoi/cho-tam-giac-abc-co-dien-tich-180-cm2-tren-cac-canh-ab-bc-ca-lan-luot-lay-cac-diem-m-n-p-sao-cho-am-23-ab-bn-34-bc-va-cp-13-ca-tinh-di.8088189515587
Đúng 0
Bình luận (0)
Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.
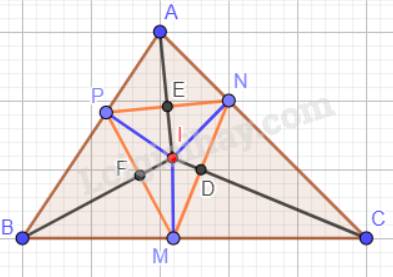
Gọi D là giao điểm của IC và MN; E là giao điểm của IA và PN; F là giao điểm của IB và PM.
Ta có: Trong tam giác ABC, ba đường phân giác cùng đi qua một điểm và điểm đó cách đều ba cạnh của tam giác hay IM = IN = IP.
Xét tam giác vuông INC và tam giác vuông IMC:
IC chung;
IN = IM.
Vậy \(\Delta INC = \Delta IMC\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {MIC} = \widehat {NIC}\)( 2 góc tương ứng).
Tương tự: \(\Delta IPA = \Delta INA\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIA} = \widehat {NIA}\)( 2 góc tương ứng).
\(\Delta IPB = \Delta IMB\)(cạnh huyền – cạnh góc vuông) nên \(\widehat {PIB} = \widehat {MIB}\)( 2 góc tương ứng).
Xét hai tam giác IDN và IDM có:
ID chung;
\(\widehat {NID} = \widehat {MID}\);
IN = IM.
Vậy \(\Delta IDN = \Delta IDM\)(c.g.c)
\(\Rightarrow DN = DM\) ( 2 cạnh tương ứng);
\(\widehat {IDN} = \widehat {IDM}\) ( 2 góc tương ứng)
Mà \(\widehat {IDN} + \widehat {IDM}=180^0\) ( 2 góc kề bù)
\(\Rightarrow \widehat {IDN} = \widehat {IDM}= 180^0:2=90^0\).
Suy ra: IC là đường trung trực của cạnh MN.
Tương tự ta có:
IA là đường trung trực của cạnh PN; IB là đường trung trực của cạnh PM.
Đúng 0
Bình luận (0)