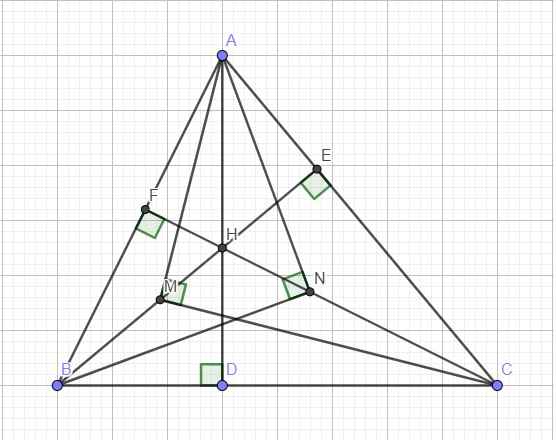
Trên mặt phẳng, cho đoạn thẳng BC=2a(a>0), lấy 1 điểm A bất kì sao cho tam giác ABC nhọn. Các đường cao AD,BR,CF cắt nhau tại H (D,E,F lần lượt nắm trên các cạnh BC, CA, AB). Trên các đoạn HB, HC lần lượt lấy M, N sao cho \(\widehat{AMC}=\widehat{BNA}=90^o\)
a) chứng minh tam giác AMN cân
b) tìm GTLN của BN.CM theo a
Tính chất cơ bản của tam giác với 3 đường cao: \(\Delta AEF\sim\Delta ABC\) (bài toán quen thuộc chắc em tự c/m được)
\(\Rightarrow AF.AB=AE.AC\)
Trong tam giác vuông ABN với đường cao NF:
\(AN^2=AF.AB\)
Trong tam giác vuông ACM:
\(AM^2=AE.AC\)
\(\Rightarrow AM^2=AN^2\Rightarrow AM=AN\)
b. Hệ thức lượng: \(BN^2=BF.AB\) ; \(CM^2=CE.AC\)
\(\Delta ABD\sim\Delta CBF\) (2 tam giác vuông chung góc B)
\(\Rightarrow\dfrac{AB}{BC}=\dfrac{BD}{BF}\Rightarrow BF.AB=BD.BC\) (1)
Hoàn toàn tương tư, \(\Delta ADC\sim\Delta BEC\Rightarrow CE.AC=CD.BC\) (2)
Cộng vế (1) và (2) \(\Rightarrow BF.AB+CE.AC=\left(BD+CD\right)BC=BC^2\)
\(\Rightarrow BN^2+CM^2=BC^2\)
\(\Rightarrow BN.CM\le\dfrac{1}{2}\left(BN^2+CM^2\right)=\dfrac{1}{2}BC^2=2a^2\)
Dấu "=" xảy ra khi tam giác cân tại A