Tam giác ABC có các cạnh là AB = 7cm; BC = 6cm; CA = 3cm.
Tam giác A'B'C' đồng dạng với tam giác ABC và có cạnh nhỏ nhất là 7,5cm. Chu vi của tam giác A'B'C' là
NT
Những câu hỏi liên quan
Cho tam giác ABC có BC= 1cm; AC= 7cm và độ dài cạnh AB là một số nguyên (cm).Tính độ dài AB và cho biết tam giác ABC là tam giác gì?
A. AB= 7cm và tam giác ABC vuông tại A
B. AB= 7cm và tam giác ABC cân tại A
C. AB= 7cm và tam giác ABC vuông cân tại A
D. AB= 8cm và tam giác ABC vuông tại B
Xem thêm câu trả lời
Tam giác ABC có AB = 3cm, BC = 5cm, CA= 7cm. Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 4,5cm.Tính các cạnh còn lại của tam giác A'B'C'.
Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất bằng 4,5 nên cạnh nhỏ nhất của △ A'B'C' tương ứng với cạnh AB nhỏ nhất của △ ABC
Giả sử A'B' là cạnh nhỏ nhất 'của Δ A'B'C'
Vì
△
A'B'C' đồng dạng
△
ABC nên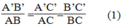 
Thay AB = 3(cm), AC = 7(cm), BC = 5(cm), A'B' = 4,5(cm) vào (1) ta có: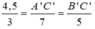 
Vậy: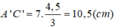 
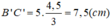
Đúng 0
Bình luận (0)
Tam giác ABC có AB = 3cm, BC = 5cm, CA= 7cm. Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 4,5cm.Tính các cạnh còn lại của tam giác A'B'C'.
QD
17 tháng 12 2016 lúc 11:53
Tam giác ABC có các cạnh là AB = 3cm; BC = 5cm; CA = 7cm.
Tam giác A'B'C' đồng dạng với tam giác ABC và có cạnh nhỏ nhất là 4,5cm. Tính chu vi của tam giác A'B'C'?
Anh mình nghĩ là như thế này. Mà ko biết đúng hay sai .
Ta có : \(\frac{A'B'}{AB}=\frac{B'C'}{BC}=\frac{C'A'}{CA}\)
Suy ra : \(\frac{4,5}{3}=\frac{B'C'}{5}=\frac{C'A'}{7}\)
\(\Rightarrow B'C'=\frac{5.4,5}{3}=7,5\)
\(C'A'=\frac{7.4,5}{3}=10,5\)
Chu vi tam giác A'B'C' là :
4,5 + 7,5 + 10,5 = 22,5 cm
Đ/s : 22,5 cm
Đúng 0
Bình luận (1)
Cho tam giac ABC,AB=cm,AC10cm,BC=7cm Tam giác A'B'C' đồng dạng với tam giác ABC,có cạnh lớn nhất là 15cm.Tính các cạnh còn lại của tam giác A'B'C'
vé hình, dùng định lí talet áp dụng tàm giác đồng dạng
Đúng 0
Bình luận (0)
Tam giác ABC có AB = 3cm, BC = 5cm và CA = 7cm. Tam giác A'B'C' đồng dạng với tam giác ABC có cạnh nhỏ nhất là 4,5 cm.
Tính các cạnh còn lại của tam giác A'B'C' ?
Cho tam giác ABC có các cạnh
A
B
6
c
m
,
B
C
8
c
m
,
A
C
7
c
m
.
So sánh các góc của tam giác ABC. A. ∠A ∠B ∠C B. ∠A ∠C ∠B C. ∠C ∠B ∠A D. ∠C ∠A ∠B
Đọc tiếp
Cho tam giác ABC có các cạnh A B = 6 c m , B C = 8 c m , A C = 7 c m . So sánh các góc của tam giác ABC.
A. ∠A > ∠B > ∠C
B. ∠A > ∠C > ∠B
C. ∠C > ∠B > ∠A
D. ∠C > ∠A > ∠B
Có AB < AC < BC ⇒ ∠C < ∠B < ∠A hay . ∠A > ∠B > ∠C . Chọn A
Đúng 0
Bình luận (0)
Cho tam giác ABC có cạnh A B = 8 c m , B C = 8 c m , A C = 7 c m . So sánh các góc của tam giác ABC
A. ∠A > ∠B = ∠C
B. ∠A > ∠C > ∠B
C. ∠C > ∠B > ∠A
D. ∠C = ∠A > ∠B
Vì AB = BC > AC ⇒ ∠C = ∠A > ∠B . Chọn D
Đúng 0
Bình luận (0)
Cho tam giác ABC có độ dài các cạnh
A
B
8
c
m
,
A
C
7
c
m
,
B
C
4
c
m
.
So sánh các góc của tam giác ABC. A. ∠B ∠A ∠C B. ∠C ∠B ∠A C. ∠C ∠A ∠B D. ∠C ∠B ∠A
Đọc tiếp
Cho tam giác ABC có độ dài các cạnh A B = 8 c m , A C = 7 c m , B C = 4 c m . So sánh các góc của tam giác ABC.
A. ∠B > ∠A > ∠C
B. ∠C < ∠B < ∠A
C. ∠C > ∠A > ∠B
D. ∠C > ∠B > ∠A
Vì BC < AC < AB ⇒ ∠A < ∠B < ∠C hay ∠C > ∠B > ∠A . Chọn D
Đúng 0
Bình luận (0)
cho tam giác abc có ab=3cm ac=7cm tính độ dài cạnh bc biết độ dài cạnh này là nguyên tố. tam giác abc là tam giác gì
Xét ΔABC có
AC-AB<BC<AB+AC
\(\Leftrightarrow7-3< BC< 7+3\)
\(\Leftrightarrow4< BC< 10\)
\(\Leftrightarrow BC\in\left\{5;7\right\}\)
Đúng 0
Bình luận (0)
Ta có: AC + AB > BC > AC - AB(bất đẳng thức tam giác)
=>7 + 3 > BC > 7 - 3
10 > BC > 4
Mà độ dài BC là số nguyên tố nên BC\(\in\)(5,7)
Với BC =5 thì \(\Delta ABC\) là tam giác thường
Với BC =7 thì \(\Delta ABC\) là tam giác cân
Đúng 1
Bình luận (0)
Giải:
Xét ΔABC có:
AC-AB<BC<AB+AC
+7 − 3 < BC < 7 + 3 ⇔ 7 − 3 < BC < 7+3
+4 < BC < 10 ⇔ 4 < BC < 10
+BC ∈ {5;7}
Đúng 0
Bình luận (0)