Cho tam giác ABC có \(\widehat{B}=90^0\)và AB < AC; AD là đường phân giác của tam giác ABC. Trên cạnh AC lấy điểm E sao cho AE = AB. Chứng minh rằng:
1. DB = DE
2. DB < DC
TV
Những câu hỏi liên quan
Tam giác vuông ABC (\(\widehat{A}=90^0\)) có AB = 6cm, AC = 8cm và tam giác vuông A'B'C' (\(\widehat{A'}=90^0\)) có A'B' = 9cm, B'C' = 15 cm
Hỏi rằng hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không ? Vì sao ?
+) Trong tam giác vuông A’B’C’ có \(\widehat{A'}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
A′B′2+A′C′2 =B′C′2
=> A′C′2=B′C′2−A′B′2=152−92=144
=> A’C’ =12 (cm)
Trong tam giác vuông ABC có \(\widehat{A}=90^0\)
Áp dụng định lí Pi-ta-go, ta có:
BC2=AB2+AC2= 62+82=100
Suy ra: BC = 10 (cm)
Ta có: \(\dfrac{A'B'}{AB}=\dfrac{9}{6}=\dfrac{3}{2}\)
\(\dfrac{A'C'}{AC}=\dfrac{12}{8}=\dfrac{3}{2}\)
\(\dfrac{B'C'}{BC}=\dfrac{15}{10}=\dfrac{3}{2}\)
Suy ra: \(\dfrac{A'B'}{AB}=\dfrac{A'C'}{AC}=\dfrac{B'C'}{BC}=\dfrac{3}{2}\)
Vậy ∆ A’B’C’ đồng dạng với ∆ ABC
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\widehat{B}>90^0\), điểm D nằm giữa B và C.
Chứng minh rằng : AB < AD < AC
Xét ΔABD có \(\widehat{B}>90^0\)
nen AD là cạnh lớn nhất
=>AB<AD(1)
XétΔADC có \(\widehat{ADC}>90^0\)
nên AC là cạnh lớn nhất
=>AD<AC(2)
Từ (1) và (2) suy ra AB<AD<AC
Đúng 0
Bình luận (0)
Các tam giác vuông ABC và DEF có \(\widehat{A}=\widehat{D}=90^0;AC=DF;\widehat{B}=\widehat{E}\). Các tam giác vuông đó có bằng nhau không ?
Xét hai tam giác vuông ABC và DEF có:
AC = DF (gt)
\(\widehat{ABC}=\widehat{DEF}\) (gt)
Vậy: \(\Delta ABC=\Delta DEF\left(cgv-gn\right)\).
Đúng 0
Bình luận (0)
CHO TAM GIÁC ABC CÓ\(\widehat{C}< \widehat{B}< 90^0\).LẤY D THUỘC CẠNH AB,E THUỘC CẠNH AC SAO CHO BD=CE. ĐƯỜNG THẲNG DE VÀ BC CẮT NHAU Ở F. CM \(\frac{AB}{AC}=\frac{FE}{FD}\)
Trong mặt phẳng của hệ tọa độ Oxy , cho tam giác ABC có AB AC , widehat{BAC} 90 độ . Biết M(1 ; -1 ) là trung điểm của cạnh BC và G ( dfrac{2}{3} ; 0 ) là trọng tâm tam giác ABC . Khi đó , A ( xa ; yb ) , B ( xa ; yb ) (xb 0 ) . Tính 2019 x2A + y A + 2xB - 3yB.
Đọc tiếp
Trong mặt phẳng của hệ tọa độ Oxy , cho tam giác ABC có AB = AC , \(\widehat{BAC}\) = 90 độ . Biết M(1 ; -1 ) là trung điểm của cạnh BC và G ( \(\dfrac{2}{3}\) ; 0 ) là trọng tâm tam giác ABC . Khi đó , A ( xa ; yb ) , B ( xa ; yb ) (xb < 0 ) . Tính 2019 x2A + y A + 2xB - 3yB.
Cho tam giác ABC có trung tuyến AM, \(\widehat{AMB}=\alpha\), AC=b, AB=c, S là diện tích tam giác ABC. Chứng minh rằng với \(0^0< \alpha< 90^0\)thì b>c
Cho tam giác vuông ABC, \(\widehat{A}=90^0;\widehat{C}=30^0\) và đường phân giác BD (D thuộc cạnh AC)
a) Tính tỉ số \(\dfrac{AD}{CD}\)
b) Cho biết độ dài AB = 12,5cm. hãy tính chu vi và diện tích của tam giác ABC
a) Ta có ΔABC vuông tại A và \(\widehat{C}\) = 300
\(\Rightarrow\)AB = 1/2BC ⇒ BC = 2AB
Vì BD là phân giác ⇒ DA/DC = AB/BC = AB/2AB =1/2
b) AB = 12,5 cm \(\Rightarrow\) BC = 25 cm Áp dụng định lí pitago vào tam giác ABC vuông tại A ta có : AC2= BC2 – AB2 = 252 – 12,52 AC = 21,65 (cm) CABC = AB+ BC+ CA =12,5+25+21,65 = 59,15(cm) SABC = 1/2AB.AC =1/2.12,5.21,65 = 135,31 (cm2)
\(\Rightarrow\)AB = 1/2BC ⇒ BC = 2AB
Vì BD là phân giác ⇒ DA/DC = AB/BC = AB/2AB =1/2
b) AB = 12,5 cm \(\Rightarrow\) BC = 25 cm Áp dụng định lí pitago vào tam giác ABC vuông tại A ta có : AC2= BC2 – AB2 = 252 – 12,52 AC = 21,65 (cm) CABC = AB+ BC+ CA =12,5+25+21,65 = 59,15(cm) SABC = 1/2AB.AC =1/2.12,5.21,65 = 135,31 (cm2)
Đúng 0
Bình luận (1)
Vẽ tam giác ABC biết \(\widehat{A}=90^0;AB=AC=3cm\). Sau đó đo các góc B và C ?
Giải:
Cách vẽ:
- Vẽ góc \(\widehat{xAy}\)=900
- Trên tia Ax vẽ đoạn thẳng AB= 3cm,
- Trên tia Ay vẽ đoạn thẳng AC= 3cm,
- Vẽ đoạn BC.
Ta vẽ được đoạn thẳng BC.
Ta đo các góc B và C ta được \(\widehat{B}=\widehat{C}\)=450
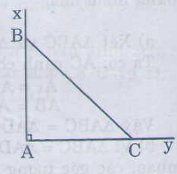
Đúng 0
Bình luận (0)
Cho tam giác ABC có \(\widehat{B}>90^o\),điểm D nằm giữa B và C.CMR AB<AD<AC
Cho tam giác ABC có góc A \(\ne\)900, góc B và C < 900. Kẻ AH \(\perp\)BC. Gọi D, E lần lượt là điểm đối xứng của H qua AB, AC. Gọi I, K lần lượt là giao điểm của DE với AB, AC. Tính số đo \(\widehat{AIC,}\widehat{AKB}\).
Gọi Q và O lần lượt là giao điểm cuarDH và AB; HE và AC. ( Điểm Q chưa ký hiệu trên hình vì nhỏ quá nhé ).
Ta dễ dàng chứng minh được: tam giác vuông KHO = tam giác vuông KEO ( hai cạnh góc vuông )
=> \(\widehat{HKO}=\widehat{EKO}\)<=> KO là phân giác ngoài của tam giác IKH ( 1 )
Do \(AH\perp BC\)=> HC là phân giác ngoài của tam giác IKH ( 2 )
Mà KO cắt HC tại C ( 3 ). Từ ( 1 ); ( 2 ) và ( 3 ) => IC là phân giác trong của tam giác IKH <=> \(\widehat{HIC}=\widehat{CIK}=\frac{1}{2}\widehat{HIE}\)( * )
Ta dễ dàng chứng minh được : tam giác vuông DIQ = tam giác vuông HIQ ( hai cạnh góc vuông ) => \(\widehat{DIQ}=\widehat{QIH}=\frac{1}{2}\widehat{DIH}\)( # )
Do D; I ; E thẳng hàng ( theo bài ra ) nên \(\widehat{DIH}+\widehat{HIE}=180^o\)( % )
Từ ( * ); ( # ) và ( % ) => \(\widehat{QIH}+\widehat{HIC}=\frac{1}{2}\widehat{DIH}+\frac{1}{2}\widehat{HIE}\Leftrightarrow\widehat{BIC}=\frac{1}{2}\left(\widehat{DIH}+\widehat{HIE}\right)=\frac{1}{2}.180^o=90^o\)
Do hai góc AIC và BIC là hai góc nằm ở vị trí kề bù nên : \(\widehat{AIC}+\widehat{BIC}=180^o\Leftrightarrow\widehat{AIC}=180^o-\widehat{BIC}=180^o-90^o=90^o\)
Tương tự, ta chứng minh được \(\widehat{AKB}=90^o\)Vậy số đo \(\widehat{AIC},\widehat{AKB}\)đều là \(90^o.\)
Đúng 0
Bình luận (0)





