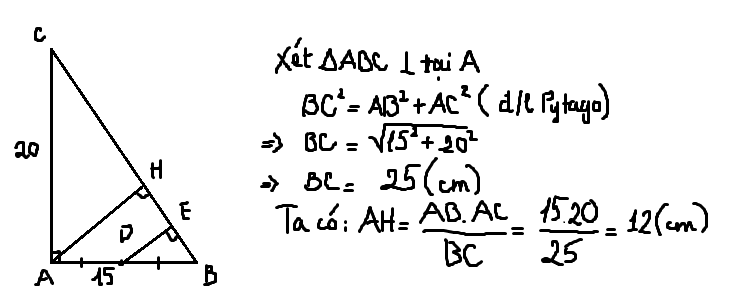Cho ∆ABC vuông tại A, đường cao AH. Gọi D;E lần lượt là hình chiếu của H trên AB; AC. a) Tính DE biết BH = 3cm, CH = 6cm b) Chứng minh AD.AB=AE. AC c) Chứng minh 1/𝐷𝐻2 = 1/𝐵𝐻2 + 1/𝐴𝐵2 + 1/𝐴𝐶2 .
JB
Những câu hỏi liên quan
Cho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH CEHCho tam giác ABC vuông tại A có đường cao AH. Tia...
Đọc tiếp
Cho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEHCho tam giác ABC vuông tại A có đường cao AH. Tia phân giác góc BAH cắt BH tại D. Gọi M là trung điểm AB. E là giao điểm MD và AH. Chứng minh DAH = CEH. AB>AC
1 phần thôi nhé
Nối BE, Gọi P là giao điểm của AD với BE.
Áp dụng định lí Ceva cho tam giác ABE => AH/HE=BP/PE=> HP//AB(1).
Từ (1)=> Tam giác AHP cân tại H=> AH=HP.(2)
Ta cần chứng minh AD//CE <=> DP//CE <=> BD/BC=BP/BE <=> BD/BC=1-(EP/BE).(3)
Mà EP/BE=HP/AB (do (1))=> EP/BE= AH/AB=HD/DB (do (2) và tc phân giác). (4)
Khi đó (3)<=> BD/BC=1-(HD/DB) hay (BD/BC)+(HD/DB)=1 <=> BD^2+HD*BC=BC*DB
<=> BD^2+HD*BC= (BD+DC)*BD <=> BD^2+HD*BC= BD^2+BD*DC <=> HD*BC=BD*DC
<=> HD/DB=CD/BC <=> AH/AB=CD/BC. (5)
Chú ý: Ta cm được: CA=CD (biến đổi góc).
Nên (5) <=> AH/AB=CA/BC <=> Tg AHB đồng dạng Tg CAB.( luôn đúng)
=> DpCm.
Đúng 0
Bình luận (0)
cho tam giác vuông ABC tại A, đường cao AH. Gọi I là trung điểm của AH. Đường vuông góc với BC tại C cắt đường thẳng BI tại D. CMR: DA=DC
cho tam giác ABC vuông tại A, đường cao AH. Gọi I là trung điểm của AH. Đường vuông góc với BC tại C cắt BI tại D. Chứng minh DA=DC
cho tam giác ABC vuông tại A đường cao AH gọi D là trung điểm ACvẽ DE vuông góc BC tại E CM: AHED là hình thang vuông
 Do AH là đường cao của ∆ABC
Do AH là đường cao của ∆ABC
⇒ AH ⊥ BC
Mà DE ⊥ BC (gt)
⇒ AH // DE
Lại có DE ⊥ BC (gt)
⇒ ∠DEH = 90⁰
Tứ giác AHED có:
AH // DE (cmt)
⇒ AHED là hình thang
Mà ∠DEH = 90⁰ (cmt)
⇒ AHED là hình thng vuông
Đúng 0
Bình luận (1)
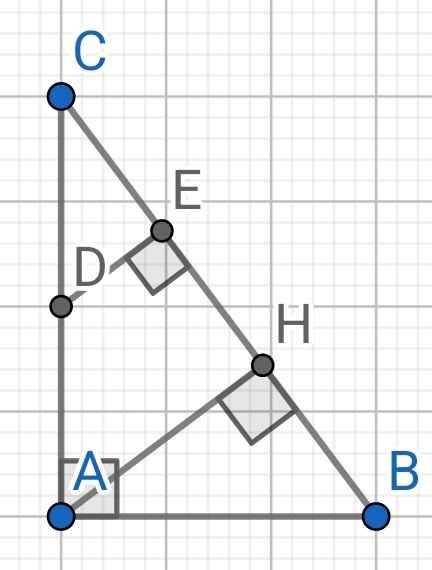
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D, E theo thứ tự là chân đường vuông góc kể từ H đến AB, AC. Chứng minh rằng AH = DE
Xét tứ giác ADHE, ta có:
∠ A = 90 0 (gt)
∠ (ADH) = 90 0 (vì HD ⊥ AB)
∠ (AEH) = 90 0 (Vì HE ⊥ AC)
Suy ra tứ giác ADHE là hình chữ nhật (vì có 3 góc vuông)
Vậy AH = DE (tính chất hình chữ nhật)
Đúng 0
Bình luận (0)
CHo tam giác ABC vuông tại A đường cao AH. Gọi D,E lần lượt là trung điểm của các đoạn thẳng AH, BH.CMR: CD vuông AE.
Bài 1:Cho tam giác ABC vuông tại A, đường cao AH và AB = 15cm, AC = 20cm. Gọi D là trung điểm của AB. Qua D kẻ DE vuông góc với BC tại E.
a) Tính BC, AH
a:\(BC=\sqrt{AB^2+AC^2}=25\left(cm\right)\)
\(AH=\dfrac{AB\cdot AC}{BC}=\dfrac{15\cdot20}{25}=12\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Gọi D,E theo thứ tự là trung điểm của BH, AH. Chứng minh : CE vuông góc AD
cho tam giác abc vuông tại a(ab<ac), đường cao ah. gọi k là trung điểm ah. vẽ đường tròn tâm K, đường kính AH cắt ab và ac lần lượt tại d,e. a, chứng minh adhe là hình chữ nhật và ad.ab=ae.ac ; b, gọi O là trung điểm BC. Chứng minh AO vuông góc với DE. c, giả sử AB = 15cm, AC = 20cm. Trung trực của BC cắt nhau tại I. Tính bán kính đường tròn ngoại tiếp tứ giác BDEC
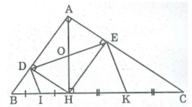
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH 12cm; BC 18cmBài 2: Cho tam giác ABC (AC AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:a, DE là đường trung trực của AHb, DEKH là hình thang cânBài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AHb, CM: AI vuôn...
Đọc tiếp
Bài 1: Cho tam giác ABC cân tại A, đường cao AH. Gọi I là trung điểm của AH. E là giao điểm của BI và AC. Tính các độ dài AE và EC biết AH =12cm; BC = 18cm
Bài 2: Cho tam giác ABC (AC > AB), đường cao AH. Gọi D,E,K theo thứ tự là trung điểm của AB, AC,BC. CMR:
a, DE là đường trung trực của AH
b, DEKH là hình thang cân
Bài 3: Cho tam giác ABC cân tại A, đường cao AH. Gọi D là chân đường vuông góc kẻ từ H đến AC. I là trung điểm của HD.
a, Gọi M là trung điểm của CD. CMR: MI vuông góc với AH
b, CM: AI vuông góc với BD