Cho hình vẽ bên dưới.Biết tam giác ABC có góc A vuông; AB=3.6 cm , AC = 4, 8 cm và AH = 2, 88 cm. Tính chu vi tam giác ABC .
H24
Những câu hỏi liên quan
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, mặt bên (SBC) là tam giác đều và nằm trong mặt phẳng vuông góc đáy (tham khảo hình vẽ bên). Tang góc giữa đường thẳng SA và mặt phẳng (ABC) bằng A.
3
B.
6
3
C.
6
2
D.
3
3
Đọc tiếp
Cho hình chóp S.ABC có đáy là tam giác vuông tại A, mặt bên (SBC) là tam giác đều và nằm trong mặt phẳng vuông góc đáy (tham khảo hình vẽ bên). Tang góc giữa đường thẳng SA và mặt phẳng (ABC) bằng
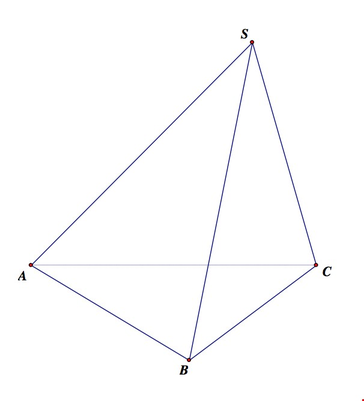
A. 3
B. 6 3
C. 6 2
D. 3 3
Cho hình vẽ bên dưới.Biết diện tích hình thang ABCE là 211,2m vuông.Diện tích tam giác ECD là 24,32m vuông.AE=18,92m,ED=3,8m.Tính độ dài cạnh BC.
Chiều cao hình tam giác EDC là: 24,32:3,8=6,4(m)
=>Nếu chiều cao hình tấm giác EDC =6,4 m thì chiều cao của hình thang ABCE cũng=6,4m
Tổng hai đáy hình tháng ABCE là: 211,2×2:6,4=66(m)
Độ dài cạnh BC là:
66-18,92=47,08(m)
ĐS: 47,08m
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB a. Cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng
60
o
(tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và SC bằng A. a B.
a
2
2
C.
a...
Đọc tiếp
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại B, AB =a. Cạnh bên SA vuông góc với mặt phẳng đáy, góc tạo bởi hai mặt phẳng (ABC) và (SBC) bằng 60 o (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng AB và SC bằng
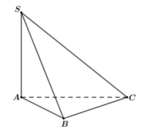
A. a
B. a 2 2
C. a 3 2
D. a 3 3
Chọn C
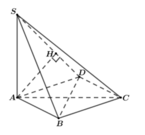
Xác định được
![]()
Khi đó ta tính được
![]()
Trong mặt phẳng (ABC) lấy điểm D sao cho ABCD là hình chữ nhật => AB//(SCD) nên
![]()
![]()
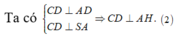
Từ (1) và (2) suy ra
![]()
Xét tam giác vuông SAD có
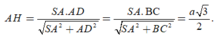
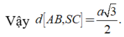
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc nhọn tại A. Vẽ bên ngoài tam giác ABC các tam giác vuông cân đỉnh A là ABD và ACE. Gọi M là trung điểm của BC. Chứng minh rằng AM vuông góc với DE.
Cho tam giác abc có a>90 độ bên ngoài tam giác abc vẽ tam giác abd và tam giác ace vuông cân tại a Chứng minh CD=BE và CD vuông góc BE
Xét \(\Delta ACD\)và \(\Delta ABE\)có :
Chung góc A
AC = AE
AD = AB
Vậy \(\Delta ACD=\Delta ABE\)\(\left(c.g.c\right)\)\(\Rightarrow CD=BE\)( hai cặp cạnh tương ứng bằng nhau )
Tớ chỉ biết có vậy thôi ! Hãy nhớ tớ là người đầu tiên làm cho bạn ! NÊN !
Đúng 0
Bình luận (0)
Cho hình vẽ bên biết ∆ABC cân tại A, AH vuông góc BC,
AH = 8cm, BC = 12cm, CH = 5cm, AH = √75(cm)
a) Tính AC
b) Tam giác AHC có vuông không? Tại sao?
Xét tam giác AHC: AH vuông góc BC (gt).
\(\Rightarrow\) Tam giác AHC vuông tại H.
Xét tam giác ABC cân tại A:
AH là đường cao (AH vuông góc BC).
\(\Rightarrow\) AH là trung tuyến (Tính chất tam giác cân).
\(\Rightarrow\) H là trung điểm của BC.
\(\Rightarrow\) \(BH=HC=\dfrac{BC}{2}=\dfrac{12}{2}=6\left(cm\right).\)
Xét tam giác AHC vuông tại H:
\(AH^2+HC^2=AC^2\left(Pytago\right).\)
\(\Rightarrow\sqrt{75}^2+6^2=AC^2.\Leftrightarrow AC^2=111.\\ \Rightarrow AC=\sqrt[]{111}\left(cm\right).\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có góc A nhọn. Vẽ bên ngoài các tam giác vuông cân đỉnh A là tam giác ABD và tam giác ACE. Gọi M là trung điểm BC. Chứng minh: AM vuông góc với BD.
AM vuông góc với DE chứ.
\(\overrightarrow{AM}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right);\overrightarrow{DE}=\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(\Rightarrow\overrightarrow{AM}.\overrightarrow{DE}=\dfrac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)\left(\overrightarrow{AE}-\overrightarrow{AD}\right)\)
\(=\dfrac{1}{2}\left(\overrightarrow{AB}.\overrightarrow{AE}-\overrightarrow{AC}.\overrightarrow{AD}-\overrightarrow{AB}.\overrightarrow{AD}+\overrightarrow{AC}.\overrightarrow{AE}\right)\)
\(=\dfrac{1}{2}\left[AB.AE.cos\left(\widehat{BAC}+90^o\right)-AC.AD.cos\left(\widehat{BAC}+90^o\right)-AB.AD.cos90^o+AC.AE.cos90^o\right]\)
\(=0\)
\(\Rightarrow AM\perp DE\)
Đúng 0
Bình luận (1)
Cách giải lớp 8 (khá loằng ngoằng):
 Vẽ hbh AEID , AJED
Vẽ hbh AEID , AJED
Gọi O là trung điểm IA
Ta có: góc BAC = góc IAD (cùng bù góc DAE)
Xét tam giác ADI và ABC có:
góc BAC = góc IAD (cmt)
AB = AD (gt)
AC = DI (do cùng bằng AE)
=> 2 tam giác bằng nhau (c-g-c)
=> BC = IA và góc ACM = góc AID
=> MC = OA (vì BC = 2MC và IA = 2OA)
Xét tam giác AMC và AOE có:
AC = AE (gt)
MC = OA (cmt)
góc ACM = góc OAE ( cùng bằng góc AID)
=> 2 tam giác bằng nhau (c-g-c)
=> góc MAC = góc OEA
Mà góc OEA = góc EAJ (sole tr vì DE // AJ)
=> góc MAC = góc EAJ
Ta có :góc EAJ + góc JAC = 90°
=> góc MAC + góc JAC = 90°
Hay góc MAJ = 90°
=> AM vuông góc AJ
Mà AJ // DE
=> AM vuông góc DE (đpcm)
Đúng 0
Bình luận (0)
Cho khối lăng trụ ABC.ABC có đáy ABC là tam giác vuông tại A, ABa, BC2a, AB vuông góc với mặt phẳng (ABC) và góc giữa AC và mặt phẳng (ABC) bằng
30
0
(tham khảo hình vẽ bên). Tính thể tích khối lăng trụ A.
a
3
3
B.
3
a
3
C.
a...
Đọc tiếp
Cho khối lăng trụ ABC.A'B'C' có đáy ABC là tam giác vuông tại A, AB=a, BC=2a, A'B vuông góc với mặt phẳng (ABC) và góc giữa A'C và mặt phẳng (ABC) bằng 30 0 (tham khảo hình vẽ bên). Tính thể tích khối lăng trụ
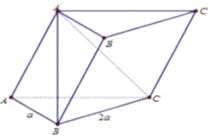
A. a 3 3
B. 3 a 3
C. a 3
D. a 3 6
Cho hình vẽ bên biết ∆ABC cân tại A, AH vuông góc BC,
AH = 8cm, BC = 12cm, CH = 5cm, AH = √75(cm)
a) Tính CH và AC
b) Tam giác AHC có vuông không? Tại sao?
a+b, CH có rồi mà bạn
Có AH vuông BC (gt) => tam giác AHC vuông tại H
Theo định lí Pytago tam giác AHC vuông tại H
\(AC=\sqrt{AH^2+HC^2}=10cm\)
Đúng 0
Bình luận (0)





