Mặt phẳng (P) thay đổi luôn đi qua M (1; 2; 3). Biết (P) cắt các tia Ox, Oy, Oz tại A, B, C. Tìm GTNN của thể tích OABC (Vmin).
A. Vmin = 24.
B. Vmin = 27.
C. Vmin = 9 14
D. Vmin = 36.
Cho hai đường thẳng ∆ và ∆ ′ chéo nhau nhận AA’ làm đoạn vuông góc chung, trong đó A thuộc ∆ và A’ thuộc ∆ ′ . Gọi (P) là mặt phẳng qua A vuông góc với ∆ ′ và d là hình chiếu vuông góc của ∆ trên mặt phẳng (P). Đặt AA’ = a, góc nhọn giữa ∆ và d là α . Mặt phẳng (Q) song song với mặt phẳng (P) cắt ∆ và ∆ ′ lần lượt tại M và M’. Gọi M 1 là hình chiếu vuông góc của M lên mặt phẳng (P).
Khi x thay đổi, tâm O của mặt cầu (S) di động trên đường nào? Chứng minh rằng khi (Q) thay đổi mặt cầu (S) luôn luôn đi qua một đường tròn cố định.
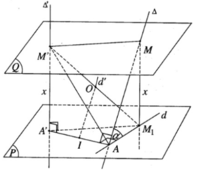
Hình tứ giác A’M’M M 1 là hình chữ nhật nên tâm O cũng là trung điểm của A’M. Do đó khi x thay đổi thì mặt phẳng (Q) thay đổi và điểm O luôn luôn thuộc đường thẳng d’ đi qua trung điểm I của đoạn AA’ và song song với đường thẳng ∆ . Vì mặt cầu tâm O luôn luôn đi qua hai điểm cố định A, A’nên nó có tâm O di động trên đường thẳng d’. Do đó mặt cầu tâm O luôn luôn chứa đường tròn tâm I cố định có đường kính AA’ cố định và nằm trong mặt phẳng cố định vuông góc với đường thẳng d’.
Cho hai đường thẳng cắt nhau Ox, Oy và 2 điểm A, B không nằm trong mặt phẳng (Ox, Oy). Biết rằng đường thẳng AB và mặt phẳng (Ox, Oy) có điểm chung I. Một mặt phẳng α thay đổi luôn chứa AB và cắt Ox tại M, cắt Oy tại N. Ta chứng minh được rằng đường thẳng MN luôn đi qua một điểm cố định khi α thay đổi. Điểm đó là
A. O
B. A
C. B
D. I
Đáp án D
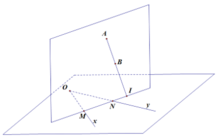
AB và mặt phẳng (Ox, Oy) luôn có điểm chung I
α chứa AB
⇒ I luôn nằm trên giao tuyến của α và (Ox, Oy) (1)
Ta lại có: α thay đổi cắt Ox tại M, Oy tại N
Xét α và (Ox, Oy) có M và N là điểm chung
⇒ MN là giao tuyến của 2 mặt phẳng (2)
(1);(2): M, N, I thẳng hàng
⇒ MN luôn đi qua I cố định
Cho tứ diện ABCD, mp (α) thay đổi đi qua các trung ddiemr I,K của các cạnh DA,DB.Các cạnh CA,CB lần lượt cắt mp(α) tại M,N
a,Gọi O là giao của Mi và Nk .Chứng minh O luôn thuộc 1 đường thẳng cố định
b, Gọi d là giao của mp(α) với mặt phẳng (OAB).Chứng minh khi mặt phẳng (α) thay đôie thì đường thẳng d luôn nằm trên 1 mp cố định và có phương không đổi
Cho tứ diện ABCD, các điểm M,N thay đổi lần lượt trên các cạnh BC,BD sao cho B C B M + B D B N = 3 Mặt phẳng (AMN) luôn đi qua điểm cố định nào sau đây?
A. Trọng tâm của tam giác BCD
B. Tâm đường tròn ngoại tiếp tam giác BCD
C. Tâm đường tròn nội tiếp tam giác BCD
D. Trực tâm của tam giác BCD
Cho tứ diện ABCD, các điểm M,N thay đổi lần lượt trên các cạnh BC,BD sao cho B C B M + B D B N = 3 . Mặt phẳng (AMN) luôn đi qua điểm cố định nào sau đây?
A.Trọng tâm của tam giác BCD.
B.Tâm đường tròn ngoại tiếp tam giác BCD.
C. Tâm đường tròn nội tiếp tam giác BCD.
D. Trực tâm của tam giác BCD.
Trong không gian Oxyz, cho mặt phẳng (P) thay đổi nhưng luôn đi qua hai điểm là A(2;0;0), M(1;1;1). Cho (P) cắt các tia Oy, Oz lần lượt tại các điểm B, C (khác O). Viết phương trình mặt phẳng (P) sao cho thể tích của từ diện OABC nhỏ nhất.
A. x 2 + y 3 + z 6 = 1
B. x 2 + y 4 + z 4 = 1
C. x 2 + y 6 + z 3 = 1
D. 2x-y-z-2=0
Đáp án B
Gọi B(0; b; 0), C(0; 0; c), trong đó b, c > 0.
Ta có: OA = 2; OB = b; OC = c
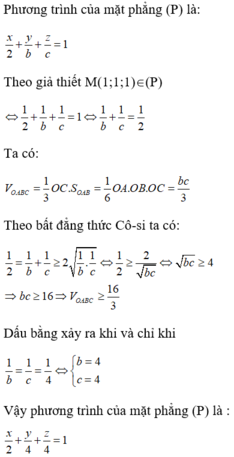
Cho mặt cầu (S) tâm O, bán kính bằng 2 và mặt phẳng (P). Khoảng cách từ O đến (P) bằng 4. Từ điểm M thay đổi trên (P) kẻ các tiếp tuyến MA, MB, MC tới (S) với A, B, C là các tiếp điểm. Biết mặt phẳng (ABC) luôn đi qua một điểm I cố định. Tính độ dài đoạn OI.
A. 3
B. 3 2
C. 1 2
D. 1
Cho mặt cầu (S) tâm O, bán kính bằng 2 và mặt phẳng (P). Khoảng cách từ O đến (P) bằng 4. Từ điểm M thay đổi trên (P) kẻ các tiếp tuyến MA;MB;MC tới (S) với A;B;C là các tiếp điểm. Biết mặt phẳng (ABC) luôn đi qua một điểm I cố định. Tính độ dài đoạn OI.
A. 3
B. 3 2
C. 1/2
D. 1
Cho hình lăng trụ tam giác ABC.A’B’C’ có AA’ = 1. Xét các điểm M,N,P thay đổi lần lượt trên các cạnh AA’, BB’, CC’ sao cho AM+BN+CP=1. Gọi I là điểm cố định mà mặt phẳng (MNP) luôn đi qua. Độ dài của vecto u → = I A → + I B → + I C → bằng
A. 3
B. 2
C. 9
D. 1