Tìm khoảng cách từ điểm C(1; 2) đến đường thẳng m: 3x + 4y – 11 = 0
PL
Những câu hỏi liên quan
tìm khoảng cách từ điểm -1 đến điểm 7 a <0
tìm khoảng cách từ điểm -2 đến điểm -8
Khoảng cách từ -1 đến 7 là
7 - ( -1) = 8
Khoảng cách từ -2 đến -8 là
-8 - -2 = -6
k nhé  Chu Quang Dũng
Chu Quang Dũng
Đúng 0
Bình luận (0)
Khoảng các từ -1 đến 7 lấy 7 - (-1 ) = 8
Khoảng cách từ -2 đến -8 là:
(-8) - (-2) = 6.
Đáp số: 8 ; 6.
Đúng 0
Bình luận (0)
8;6 nha bạn
Chúc các bạn học giỏi
Tết vui vẻ nha
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
tìm khoảng cách từ điểm -1 đến điểm 7 a <0
tìm khoảng cách từ điểm -2 đến điểm -8
điểm 1 nằm trên một đường thẳng. Điểm 2 nằm bên phải điểm 1. Điểm 3 nằm bên phải điểm 2. Khoảng cách từ điểm 1 đến điểm 2 bằng khoảng cách từ điểm 2 đến điểm 3, v.v ... Cuối cùng, điểm 101 nằm ở bên phải điểm 100 và khoảng cách từ điểm 100 đến điểm 101 nằm ở bên phải điểm 100 và khoảng cách từ điểm 100 đến điểm 101 bằng khoảng cách từ điểm 99 đến điểm 100. Nếu khoảng cách từ điểm 1 đến điểm 101 là 1m thì khoảng cách từ điểm 13 đến điểm 31 là bao nhiêu cm?
Đọc tiếp
điểm 1 nằm trên một đường thẳng. Điểm 2 nằm bên phải điểm 1. Điểm 3 nằm bên phải điểm 2. Khoảng cách từ điểm 1 đến điểm 2 bằng khoảng cách từ điểm 2 đến điểm 3, v.v ... Cuối cùng, điểm 101 nằm ở bên phải điểm 100 và khoảng cách từ điểm 100 đến điểm 101 nằm ở bên phải điểm 100 và khoảng cách từ điểm 100 đến điểm 101 bằng khoảng cách từ điểm 99 đến điểm 100. Nếu khoảng cách từ điểm 1 đến điểm 101 là 1m thì khoảng cách từ điểm 13 đến điểm 31 là bao nhiêu cm?
Trả lời:
Từ điền số 1 đến điểm 101 sẽ có: 101-1=100 khoảng bằng nhau.=> mỗi một khoảng bằng nhau có độ dài= 1m/100= 100cm/100=1cm
Từ điểm 13 đến điểm 31 có (31-13)=18 khoảng bằng nhau
=> Khoảng cách từ điểm 13 đến điểm 31 là: 18x1 cm= 18cm
Không có gì ! Chúc bạn học tốt nha
tk you so much
tìm điểm M thuộc đồ thị hàm số \(y=\dfrac{2x+1}{x-1}\) sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến trục hoành.
Đồ thị hàm nhận \(x=1\) là tiệm cận đứng
Gọi \(M\left(a;b\right)\Rightarrow b=\dfrac{2a+1}{a-1}\)
Khoảng cách từ M đến trục hoành: \(\left|y_M\right|=\left|b\right|\)
Khoảng cách từ M đến tiệm cận đứng: \(\left|x_M-1\right|=\left|a-1\right|\)
Ta được hệ: \(\left\{{}\begin{matrix}b=\dfrac{2a+1}{a-1}\\\left|b\right|=\left|a-1\right|\end{matrix}\right.\) \(\Rightarrow\left(a;b\right)=\left(0;-1\right);\left(4;3\right)\)
Có 2 điểm M thỏa mãn: \(\left[{}\begin{matrix}M\left(0;-1\right)\\M\left(4;3\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Quan sát Hình 84 và cho biết:
a) Khoảng cách từ điểm O đến đường thẳng a;
b) Khoảng cách từ điểm O đến đường thẳng b;
c) Khoảng cách từ điểm O đến đường thẳng c.
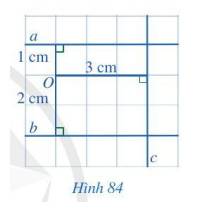
a) Khoảng cách từ điểm O đến đường thẳng a bằng 1 cm;
b) Khoảng cách từ điểm O đến đường thẳng b bằng 2 cm;
c) Khoảng cách từ điểm O đến đường thẳng c bằng 3 cm.
Đúng 0
Bình luận (0)
Trong mặt phẳng với hệ tọa độ oxy cho tam giác ABc có đỉnh B(2;-1) đường phân giác trong của góc a là đường thẳng đen ta có pt x+2y-5=0 điểm c thuộc trục tung sao cho khoảng cách từ điểm c đến đen ta =3 lần khoảng cách từ b đến đen ta tìm tọa độ c và viết pt các cạnh tam giác abc
Tìm
M
∈
C
:
y
2
x
+
1
x
-
1
sao cho khoảng cách từ điểm M đến tiệm cận đứng bằng hai lần khoảng các từ điểm M đến tiệm cận ngang A. M ( 2;5 ), M ( -2;1 ) B. M ( 2;5 ), M ( 0;-1 ) C. M ( 4;3 ), M ( -2;1 ) D. M ( 4;3 ), M ( 0;-1 )
Đọc tiếp
Tìm M ∈ C : y = 2 x + 1 x - 1 sao cho khoảng cách từ điểm M đến tiệm cận đứng bằng hai lần khoảng các từ điểm M đến tiệm cận ngang
A. M ( 2;5 ), M ( -2;1 )
B. M ( 2;5 ), M ( 0;-1 )
C. M ( 4;3 ), M ( -2;1 )
D. M ( 4;3 ), M ( 0;-1 )
M m ; 2 m + 1 m - 1 ∈ C m ≠ 1
Tiệm cận đứng x = 1 và tiệm cận ngang y = 2
Yêu cầu bài toán
⇔ a - 1 = 3 2 a + 1 a - 2 - 2 ⇔ a = 4 ⇒ M 4 ; 3 a = - 2 ⇒ M - 2 ; 1
Đáp án C
Đúng 0
Bình luận (0)
cho đường thẳng y=(m-2) x+2 (d) a, CMR: đường thẳng (d) luôn đi qua 1 điểm cố định với mọi m b,tìm già trị của m để khoảng cách từ gốc tọa độ đến đương thẳng (d) =1 c, tìm giá trị của m để khoảng cách từ gốc tọa độ đến đường thẳng m là lớn nhất
\(a,\) Gọi điểm cố định (d) luôn đi qua là \(A\left(x_0;y_0\right)\)
\(\Leftrightarrow y_0=\left(m-2\right)x_0+2\Leftrightarrow mx_0-2x_0+2-y_0=0\\ \Leftrightarrow\left\{{}\begin{matrix}x_0=0\\2-2x_0-y_0=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_0=0\\y_0=2\end{matrix}\right.\Leftrightarrow A\left(0;2\right)\)
Vậy \(A\left(0;2\right)\) là điểm cố định mà (d) lun đi qua
\(b,\) PT giao Ox,Oy: \(y=0\Leftrightarrow x=\dfrac{2}{2-m}\Leftrightarrow B\left(\dfrac{2}{2-m};0\right)\Leftrightarrow OB=\dfrac{2}{\left|m-2\right|}\\ x=0\Leftrightarrow y=2\Leftrightarrow C\left(0;2\right)\Leftrightarrow OC=2\)
Gọi H là chân đường cao từ O đến (d) \(\Leftrightarrow OH=1\)
Áp dụng HTL: \(\dfrac{1}{OH^2}=1=\dfrac{1}{OB^2}+\dfrac{1}{OC^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)
\(\Leftrightarrow m^2-4m+4+1=4\\ \Leftrightarrow m^2-4m+1=0\\ \Leftrightarrow\left[{}\begin{matrix}m=2+\sqrt{3}\\m=2-\sqrt{3}\end{matrix}\right.\)
\(c,\) Áp dụng HTL: \(\dfrac{1}{OH^2}=\dfrac{1}{OC^2}+\dfrac{1}{OB^2}=\dfrac{\left(m-2\right)^2}{4}+\dfrac{1}{4}\)
Đặt \(OH^2=t\)
\(\Leftrightarrow\dfrac{1}{t}=\dfrac{m^2-4m+5}{4}\Leftrightarrow t=\dfrac{4}{\left(m-2\right)^2+1}\le\dfrac{4}{0+1}=4\\ \Leftrightarrow OH\le2\\ OH_{max}=2\Leftrightarrow m=2\)
Đúng 1
Bình luận (0)
Cho hàm số
y
x
x
−
1
có đồ thị (C). Tìm giá trị nhỏ nhất của tổng khoảng cách từ điểm
M
∈
C
tới hai đường tiệm cận. A.
1
2
B. 2 C.
2
2
D. 1
Đọc tiếp
Cho hàm số y = x x − 1 có đồ thị (C). Tìm giá trị nhỏ nhất của tổng khoảng cách từ điểm M ∈ C tới hai đường tiệm cận.
A. 1 2
B. 2
C. 2 2
D. 1
Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.Đồ thị (C) của hàm số
y
x
+
2
x
-
3
Đọc tiếp
Tìm điểm M trên đồ thị của hàm số sao cho khoảng cách từ M đến tiệm cận đứng bằng khoảng cách từ M đến tiệm cận ngang.
Đồ thị (C) của hàm số y = x + 2 x - 3
Giả sử M( x o ; y o ) ∈ (C). Gọi d 1 là khoảng cách từ M đến tiệm cận đứng và d 2 là khoảng cách từ M đến tiệm cận ngang, ta có:
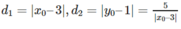
Có hai điểm thỏa mãn đầu bài, đó là hai điểm có hoành độ x o = 3 + 5 hoặc x o = 3 - 5
Đúng 0
Bình luận (0)



