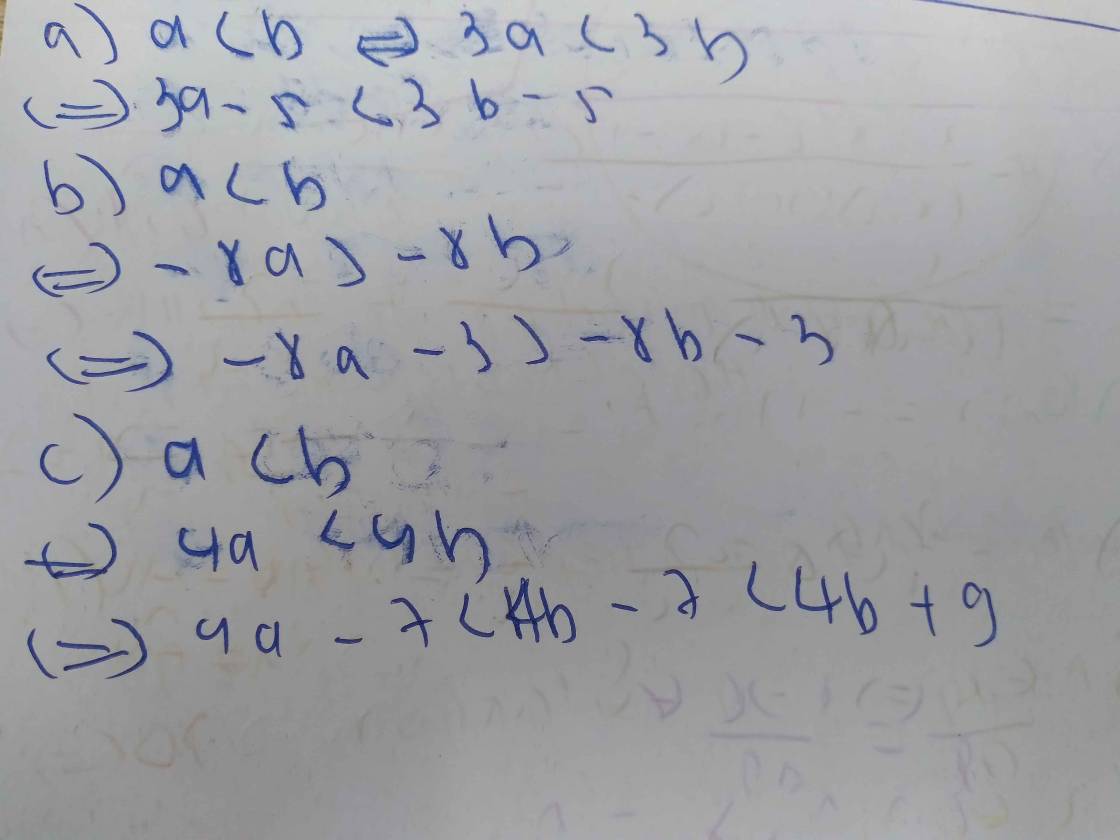\(\cdot a-4b=5\Leftrightarrow\left(a-4b\right)^2=a^2-8ab+16b^2=25\Leftrightarrow a^2+16b^2=25+8\cdot\left(-\dfrac{3}{2}\right)=13\\ \cdot a-4b=5\Leftrightarrow4b-a=-5\)

\(a,A=ab\left(4b-a\right)=-\dfrac{3}{2}\cdot\left(-5\right)=\dfrac{15}{2}\)

\(b,B=a^2+16b^2=13\left(cm.trên\right)\)

\(c,D=a+4b\)

Ta có \(\left(a+4b\right)^2=a^2+8ab+16b^2=13+8\cdot\left(-\dfrac{3}{2}\right)=1\)

\(\Rightarrow D=a+4b=1\)

a) 2/5 + 3/4 = 23/20 
b) 2/3 - 3/8 = 7/24 
c) 3/7 x 4/5 = 12/35 
d) 2/5 : 2/3 = 3/5 

\(\dfrac{2}{5}+\dfrac{3}{4}=\dfrac{8}{20}+\dfrac{15}{20}=\dfrac{22}{20}=\dfrac{11}{10}\)

\(\dfrac{2}{3}-\dfrac{3}{8}=\dfrac{16}{24}-\dfrac{9}{24}=\dfrac{7}{24}\)

\(\dfrac{3}{7}\times\dfrac{4}{5}=\dfrac{12}{35}\)

\(\dfrac{2}{5}:\dfrac{2}{3}=\dfrac{3}{5}\)

\(\dfrac{2}{5}+\dfrac{3}{4}=\dfrac{8}{20}+\dfrac{15}{20}=\dfrac{23}{20}\)

\(\dfrac{2}{3}-\dfrac{3}{8}=\dfrac{16}{24}-\dfrac{9}{24}=\dfrac{7}{24}\)

\(\dfrac{3}{7}x\dfrac{4}{5}=\dfrac{12}{35}\)

\(\dfrac{2}{5}:\dfrac{2}{3}=\dfrac{2}{5}x\dfrac{3}{2}=\dfrac{3}{5}\)

x = 4 x 3/4

x = 3

x = 4/5 + 2/5

x = 6/5

hép

Lời giải:

a.

\(-16a^4b^6-24a^5b^5-9a^6b^4=-[(4a^2b^3)^2+2.(4a^2b^3).(3a^3b^2)+(3a^3b^2)^2]\)

\(=-(4a^2b^3+3a^3b^2)^2=-[a^2b^2(4b+3a)]^2\)

\(=-a^4b^4(3a+4b)^2\)

b.

$x^3-6x^2y+12xy^2-8x^3$

$=x^3-3.x^2.2y+3.x(2y)^2-(2y)^3=(x-2y)^3$

c.

$x^3+\frac{3}{2}x^2+\frac{3}{4}x+\frac{1}{8}$

$=x^3+3.x^2.\frac{1}{2}+3.x.\frac{1}{2^2}+(\frac{1}{2})^3$

$=(x+\frac{1}{2})^3$

a) Ta có: \(-16a^4b^6-24a^5b^5-9a^6b^4\)

\(=-a^4b^4\left(16b^2+24ab+9a^2\right)\)

\(=-a^4b^4\cdot\left(4b+3a\right)^2\)

b) Ta có: \(x^3-6x^2y+12xy^2-8y^3\)

\(=x^3-3\cdot x^2\cdot2y+3\cdot x\cdot\left(2y\right)^2-\left(2y\right)^3\)

\(=\left(x-2y\right)^3\)

c) Ta có: \(x^3+\dfrac{3}{2}x^2+\dfrac{3}{4}x+\dfrac{1}{8}\)

\(=x^3+3\cdot x^2\cdot\dfrac{1}{2}+3\cdot x\cdot\left(\dfrac{1}{2}\right)^2+\left(\dfrac{1}{2}\right)^3\)

\(=\left(x+\dfrac{1}{2}\right)^3\)

a)

`a<b`

`<=>3a<3b`

`<=>3a-5<3b-5`

b)

`a<b`

`<=>-8a> -8b`

`<=>-8a-3> -8b-3`

c)

`a<b`

`<=>4a<4b`

`<=>4a+9<4b+9`

mà `4a-7<4a+9`

`<=>4a-7<4b+9`

b) /2x-3/-x=5

+) 2x-3>0⇔x>\(\dfrac{3}{2}\)

    2x-3-x=5

⇔2x-x=5+3

⇔x=8 

+) 2x-3<0⇔x<\(\dfrac{3}{2}\)

   -(2x-3)-x=5

⇔-2x+3-x=5

⇔-2x-x=5-3

⇔-3x=2

⇔x=\(\dfrac{-2}{3}\)

    S={8,\(\dfrac{-2}{3}\)}