trong mặt phẳng tọa độ oxy, cho hình vuông ABCD M là trung điểm của BC và N(-3/2; 1/2) thỏa mãn AC=4AN. Tìm A,B,C,D biết MD có phương trình x=1 và tung độ D là 1 số âm
PT
Những câu hỏi liên quan
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm cạnh BC, N là điểm trên cạnh CD sao cho CN 2ND. Giả sử M(, ) và đường thẳng AN có phương trình 2x – y – 3 0. Tìm tọa độ điểm A.
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho hình vuông ABCD. Gọi M là trung điểm cạnh BC, N là điểm trên cạnh CD sao cho CN = 2ND. Giả sử M(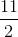 ,
,  ) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A.
) và đường thẳng AN có phương trình 2x – y – 3 = 0. Tìm tọa độ điểm A.
Phương trình đường thẳng AM: \(ax+by-\dfrac{11}{2}a-\dfrac{1}{2}b=0\left(a^2+b^2\ne0\right)\)
Giả sử cạnh hình vuông có độ dài là \(a\)
\(AM^2=\dfrac{5}{4}a^2;AN^2=\dfrac{10}{9}a^2;MN^2=\dfrac{25}{36}a^2\)
Theo định lí cos: \(cosMAN=\dfrac{AM^2+AN^2-MN^2}{2.AM.AN}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\dfrac{\left|2a-b\right|}{\sqrt{5\left(a^2+b^2\right)}}=\dfrac{\sqrt{2}}{2}\)
\(\Leftrightarrow\left(a-3b\right)\left(3a+b\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}a=3b\\3a=-b\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}AM:3x+y-17=0\\AM:x-3y-4=0\end{matrix}\right.\)
TH1: \(AM:3x+y-17=0\Rightarrow A:\left\{{}\begin{matrix}3x+y-17=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(4;5\right)\)
TH2: \(AM:x-3y-4=0\Rightarrow A:\left\{{}\begin{matrix}x-3y-4=0\\2x-y-3=0\end{matrix}\right.\Rightarrow A=\left(1;-1\right)\)
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy, cho hình chữ nhật ABCD có hình chiếu vuông góc của A lên đường thẳng BD là H(-1/5;2/5), điểm M(0;-1) là trung điểm cạnh BC và điểm N(7/5;-4/5) là trung điểm của đoạn HD. Tìm tọa độ các đỉnh của hình chữ nhật ABCD.
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có M,N lần lượt là trung điểm của các cạnh BC, CD. Tìm tọa độ đỉnh B và điểm M, biết điểm N(0; -2), M có hoành độ nguyên, đường thẳng AM có phương trình x+2y-2=0 * giúp mình với ạ, chi tiết càng tốt nhaaa
Để tìm tọa độ đỉnh B và điểm M, ta có thể sử dụng các thông tin sau:
M là trung điểm của BC, nghĩa là tọa độ của M bằng trung bình cộng của tọa độ của B và C.N là trung điểm của CD, nghĩa là tọa độ của C là (2, -2).Do ABCD là hình vuông nên độ dài các cạnh bằng nhau, suy ra AB = CD = BC = AD.Vì M có hoành độ nguyên, nên tọa độ của B và C cũng phải có hoành độ nguyên.Từ đó, ta có thể tìm tọa độ của B như sau:
Đặt tọa độ của B là (x, y).Do AB = BC, suy ra x - 1 = 1 - y, hay x + y = 2.Do AB = CD = 2, suy ra tọa độ của A là (x - 1, y + 1) và tọa độ của D là (x + 1, y - 1).Vì đường thẳng AM có phương trình x+2y-2=0, nên điểm A nằm trên đường thẳng đó, tức là x - 2y + 2 = 0.Từ hai phương trình trên, ta giải hệ: x + y = 2 x - 2y + 2 = 0Giải hệ này ta được x = 2 và y = 0, suy ra tọa độ của B là (2, 0).Tiếp theo, ta sẽ tìm tọa độ của M:
Đặt tọa độ của M là (p, q).Do M là trung điểm của BC, suy ra p = (x + r)/2 và q = (y + s)/2, với r, s lần lượt là hoành độ và tung độ của C.Ta đã biết tọa độ của C là (2, -2), suy ra r = 2 và s = -4.Từ AM có phương trình x+2y-2=0, suy ra p + 2q - 2 = 0.Với hoành độ nguyên của M, ta có thể thử các giá trị p = 1, 2, 3, ... và tính q tương ứng.Khi p = 2, ta có p + 2q - 2 = 2q = 2, suy ra q = 1.Vậy tọa độ của M là (2, 1).<đủ chi tiết luôn nhó>
Đúng 0
Bình luận (0)
Trong mặt phẳng Oxy cho hình vuông ABCD có M, N lần lượt là trung điểm của các cạnh BC, CD. Tìm tọa độ đỉnh B, điểm M biết N(0;-2), đường thẳng AM có phương trình x+2y-2=0 và cạnh hình vuông bằng 4
Gọi \(I=AM\cap BN\), \(\Delta BIM\) đồng dạng \(\Delta ABM\)
suy ra \(AM\perp BN\) nên \(BN:-2x-y+c=0\)
\(N\left(0;-2\right)\Rightarrow c=-2\Rightarrow BN:2x-y-2=0\)
Tọa độ điểm I là nghiệm hệ phương trình :
\(\begin{cases}x+2y-2=0\\2x-y-2=0\end{cases}\)\(\Leftrightarrow\begin{cases}x=\frac{6}{5}\\y=\frac{2}{5}\end{cases}\) \(\Rightarrow I\left(\frac{6}{5};\frac{2}{5}\right)\)
Từ \(\Delta ABM\) vuông : \(BI=\frac{AB.BM}{\sqrt{AB^2+BM^2}}=\frac{4}{\sqrt{5}}\)
Tọa độ điểm \(B\left(x;y\right)\) thỏa mãn \(\begin{cases}B\in BN\\BI=\frac{4}{\sqrt{5}}\end{cases}\) \(\Rightarrow\begin{cases}2x-y-2=0\\\left(\frac{6}{5}-x\right)^2+\left(\frac{2}{5}-y\right)^2=\frac{16}{5}\end{cases}\)
Giải hệ ta được \(\begin{cases}x=2\\y=2\end{cases}\) và \(\begin{cases}x=\frac{2}{5}\\y=\frac{-6}{5}\end{cases}\) Suy ra \(B\left(2;2\right)\) Loại \(\left(\frac{2}{5};-\frac{6}{5}\right)\)
Tọa đọ M(x;y) thỏa mãn \(\begin{cases}M\in AM\\IM=\sqrt{BM^2-BI^2}\end{cases}\) \(\Rightarrow\begin{cases}x+2y-2=0\\\left(x-\frac{6}{5}\right)^2+\left(y-\frac{2}{5}\right)^2=\frac{4}{5}\end{cases}\)
Giải hệ ta được : \(\begin{cases}x=2\\y=0\end{cases}\) và \(\begin{cases}x=\frac{2}{5}\\y=\frac{4}{5}\end{cases}\) suy ra \(M_1\left(2;0\right);M_2\left(\frac{2}{5};\frac{4}{5}\right)\)
Đúng 0
Bình luận (0)
Vì sao loại B (2/5;-6/5) vậy????
Đúng 0
Bình luận (0)
trong mặt phẳng với hệ tọa độ Oxy, cho hình thang vuông ABCD ( vuông tại A và B ) . Gọi M(-3,-3) N lần lược là trung điểm của AD và AB . Xác định tọa độ các đỉnh của hình thang vuông ABCD , biết phương trình các đường thẳng BD: 7x+3y+2=0, CN: x-3y=0, CN: x-y=0và đường thẳng AB đi qua điểm e (-3;1)
Đường CN có pt là x-3y=0 hay x-y=0 vậy bạn?
Đúng 0
Bình luận (0)
Trong mặt phẳng tọa độ Oxy cho hình vuông ABCD có điểm M là trung điểm của đoạn thẳng AB và N là điểm thuộc đoạn AC sao cho AN = 3NC. Biết rằng M (1; 2) và N (2; -1) và đường thẳng CD không song song với hai trục tọa độ. Đường thẳng CD đi qua điểm nào sau đây
A. (5; 0)
B. (0; 2)
C. (4; 3)
D. (7; 1)
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có I là giao điểm của hai đường chéo AC và BD. Gọi M (3; 2) và N (1; —2) lần lượt là trung điểm của đoạn AB và ID. Tìm phương trình tổng quát của đường thẳng AB.
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có I là giao điểm của hai đường chéo AC và BD. Gọi M (3; 2) và N (1; —2) lần lượt là trung điểm của đoạn AB và ID. Tìm phương trình tổng quát của đường thẳng AB.
trong mặt phẳng với hệ tọa độ oxy , cho hình thang vuông ABCD , có B=C=90độ . Phương trình các đường thẳng AC và BD lần lượt là x+2y=0 và x-y-3=0. Xác định tọa độ các đỉnh của hình thang ABCD biết trung điểm AD là m( -3/2; -3/2)
Trong mặt phẳng tọa độ Oxy, cho hình vuông ABCD có I là giao điểm của hai đường chéo AC và BD. Gọi M(3;2) và N(1;-2) lần lượt là trung điểm của các đoạn AB và ID. Tìm phương trình tổng quát của đoạn thẳng AB.
tham khảo
Gọi M' là điểm đối xứng của M qua AC. Ta có M' thuộc đường thẳng BC.
Phương trình đường thẳng MM' là 1(x - 6) - 1(y - 2) = 0 <=> x - y - 4 = 0. Gọi H = AC ∩ MM'
Tọa độ của H thỏa mãn hệ 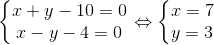 => H(7; 3)
=> H(7; 3)
H là trung điểm của MM'. Suy ra M'(8; 4)
Gọi 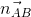 = (a; b) . Vì hai đường thẳng AB và AC tạo với nhau một góc 450 nên ta có:
= (a; b) . Vì hai đường thẳng AB và AC tạo với nhau một góc 450 nên ta có:
cos 450 = 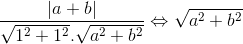 = |a + b| ⇔ ab = 0
= |a + b| ⇔ ab = 0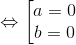
TH1: a = 0, phương trình đường thẳng AB, BC lần lượt là y = 8, x = 8. Suy ra: B(8; 8)
TH2: b = 0, phương trình đường thẳng AB, BC lần lượt là y = 5, x = 4. Suy ra: B(5; 4)
Đúng 1
Bình luận (0)




