xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 = 0
BT
Những câu hỏi liên quan
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 =0
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 =0
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 =0
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 =0
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 ; (C) : x2 + y2 - 4x + 2y + 1 =0
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây : (d) : 3x + y + m = 0 (C) : x2 + y2 - 4x + 2y + 1 =0
xét vị trí tương đối của đường thẳng (d) và đường tròn (C) sau đây :
(d) : 3x + y + m = 0
(C) : x2 + y2 - 4x + 2y + 1 =0
Cho đường thẳng d : x- y + 1 = 0 và đường tròn C : x^2 + y^2 -4x +2y -4 = 0
a) Chứng minh điểm M (2;1) nằm trong đường tròn
b) Xét vị trí tương đối giữa d và
C
c) Viết phương trình đường thẳng d' vuông góc với và cắt đường tròn tại hai điểm phân biệt sao cho khoảng cách của chúng là lớn nhất.
Đường tròn (C) tâm \(I\left(2;-1\right)\) bán kính \(R=3\)
a. \(\overrightarrow{IM}=\left(0;2\right)\Rightarrow IM=\sqrt{0^2+2^2}=2< R\Rightarrow\) M nằm trong đường tròn
b. \(d\left(I;d\right)=\dfrac{\left|2-\left(-1\right)+1\right|}{\sqrt{1^2+\left(-1\right)^2}}=2\sqrt{2}< 3\Rightarrow d\) cắt đường tròn tại 2 điểm
c. Khoảng cách giữa 2 điểm trên đường tròn là lớn nhất khi chúng nằm ở 2 mút đường kính
\(\Rightarrow\) d' đi qua tâm I
Do d' vuông góc d nên nhận (1;1) là 1 vtpt
Phương trình: \(1\left(x-2\right)+1\left(y+1\right)=0\Leftrightarrow x+y-1=0\)
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:
d1: -3x + 6y – 3 = 0;
d2: y = -2x;
d3: 2x + 5 = 4y.
Xét Δ và d1, hệ phương trình: 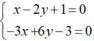 có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: 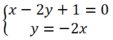 có nghiệm duy nhất (-1/5; 2/5) nên
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: 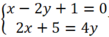 vô nghiệm
vô nghiệm
Vậy Δ // d3
Đúng 0
Bình luận (0)


