cho đt (d1) y= -6x + m-1; (d2) y= (m-1)x+3m-11
Tìm m để đt (d1) cắt đt (d2) tại 1 điểm trên trục tug. Tìm tọa độ điểm đó
Phương trình hoành độ giao điểm của \(\left(d_1\right);\left(d_2\right)\):
\(4-x=2x-5\)
\(\Leftrightarrow x=3\Rightarrow y=1\Rightarrow\left(3;1\right)\) là giao điểm của \(\left(d_1\right);\left(d_2\right)\)
Ba đường thẳng đã cho đồng quy khi và chỉ khi \(\left(3;1\right)\in\left(d_3\right)\)
\(\Leftrightarrow6-m-2m+1=0\)
\(\Leftrightarrow m=\dfrac{7}{3}\)
1. Trg mp vs hệ tọa độ Oxy , cho 2 đt \(d1:3x-4y-3=0,d2:12x+5y-12=0\).Viết pt đt phân giác góc nhọn tạo bởi 2 đt d1 và d2
2. Với giá trị nào của m thì đt \(d1:\dfrac{\sqrt{2}}{2}x-\dfrac{\sqrt{2}}{2}y+m=0\) tiếp xúc với đg tròn \(\left(C\right):x^2+y^2=1\)
1. Gọi \(M\left(x;y\right)\) là điểm bất kì nằm trên phân giác
\(\Rightarrow d\left(M;d_1\right)=d\left(M;d_2\right)\Leftrightarrow\dfrac{\left|3x-4y-3\right|}{\sqrt{3^2+\left(-4\right)^2}}=\dfrac{\left|12x+5y-12\right|}{\sqrt{12^2+5^2}}\)
\(\Leftrightarrow\left|39x-52y-39\right|=\left|60x+25y-60\right|\)
\(\Rightarrow\left[{}\begin{matrix}60x+25y-60=39x-52y-39\\60x+25y-60=-39x+52y+39\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+11y-3=0\\11x-3y-11=0\end{matrix}\right.\)
Xét \(3x+11y-3=0\) có vtpt \(\left(3;11\right)\)
Ta có: \(cos^{-1}\dfrac{\left|3.3-11.4\right|}{\sqrt{3^2+\left(-4\right)^2}.\sqrt{3^2+11^2}}=52^0>45^0\) (ktm)
\(\Rightarrow11x-3y-11=0\) là pt đường phân giác góc nhọn tạo bởi d1 và d2
2.
Phương trình d1: \(\sqrt{2}x-\sqrt{2}y+2m=0\)
Đường tròn (C) có tâm \(O\left(0;0\right)\) bán kính \(R=1\)
Đường thẳng d1 tiếp xúc với (C) khi và chỉ khi:
\(d\left(O;d_1\right)=R\)
\(\Leftrightarrow\dfrac{\left|2m\right|}{\sqrt{2+2}}=1\Leftrightarrow\left|2m\right|=2\)
\(\Rightarrow m=\pm1\)
Ta có: d1 giao d2 có tọa độ A(1;0)
nếu ta gắn A(1;0) thành O(0;0) và d2 thành trục Ox
ta có thể ngầm tưởng như sau:
áp dụng công thức tính cos giữa 2 đg thẳng d1 và d2
=> cos alpha=\(\dfrac{16}{65}\)
=> cos giữa d3: đg phân giác của góc nhọn với d2 =\(\sqrt{\dfrac{81}{130}}\)
áp dụng công thức 1+ (tan \(\dfrac{alpha}{2}\))2 =\(\dfrac{1}{cos\left(\dfrac{alpha}{2}\right)^2}\)
=> tan \(\dfrac{alpha}{2}\)=\(\sqrt{\dfrac{1}{\dfrac{81}{130}}-1}\)
tan \(\dfrac{alpha}{2}\)=\(\dfrac{7}{9}\)
mà tan alpha/2=k của d3 và d2
=> d3 có dạng y=\(\dfrac{7}{9}x\)
=> dạng d3 nếu bỏ gắn A thành O và d2 thành trục Ox sẽ có dạng
-by=\(\dfrac{7}{9}x+c\)
Vì d3 đi qua A(1;0)
=>\(-b.0=\dfrac{7}{9}.1+c\)
=>\(c=-\dfrac{7}{9}\)
=>d3:\(\dfrac{7}{9}x+by-\dfrac{7}{9}=0\)
=>\(7x+9by-7=0\)
mà cos alpha/2=\(\sqrt{\dfrac{81}{130}}=\dfrac{\text{| 7.12+9b.5 |}}{\sqrt{7^2+\left(9b\right)^2}\sqrt{12^2+5^2}}\)
\(=>\left[{}\begin{matrix}b=-\dfrac{7}{33}\\b=\dfrac{301}{219}\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}7x-\dfrac{21}{11}y-7=0\\7x+\dfrac{903}{73}-7=0\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}11X-3Y-11=0\\73X+129Y-73=0\end{matrix}\right.\)
Tính cos giữa \(11X-3Y-11=0\)
và d2 thõa mãn yêu cầu nên nhận
cos giữa \(73X+129Y-73=0\)
và d2 ko thõa mãn yêu cầu nên loại
mình mới nghỉ ra cách này thôi, nên còn nhiều thiếu xót
mình mới lớp 10 ak nha :< nên thầy cô nào xem được góp ý hộ con ạ :))
cho hàm số y = 2x+2 có đồ thhij là (d) và hàm số y = -x-1 có đồ thị là (d1)
a, vẽ (d) và (d1) trên cùng 1 mặt phẳng tọa độ trên tọa độ giao điểm của (d) và (d1) bằng phép toán
b, cho hàm số y=(m^2-11) x+m-5 (m là hàm số) co đò thị là (d2).tìm m để đt (d2) cắt đt (d).tìm m dể đt (d2) song song với đường thẳng (d)
cho 2 đt (d1) y= 2x+5 và (d2) y=(m+1)x \(+\)m-1
tìm m để 2 đt cắt nhau tại điểm có tung độ bằng 1
1 ,Cho đt y = x -3m+1 (d1) và y = 2x -2 (d2). Tìm m để hai đt (d1) và (d2) cắt nhau tại 1 điểm nằm phía trên trục hoành
2, Cho (P) y = x2 và (d) y= -2(m-2)+2m-1
xác định m để (d) cắt (P) tại 2 điểm nằm bên phải trục tung
Giúp mình với, mình cần gấpppp
Cho đường thẳng (d): y= (m-2)x+2m-3
a) vẽ đồ thị của hàm số khi m=1. Gọi đt đó là (d1)
b) Cho (d2): y= x-5. Tìm tọa độ giao điểm A của (d1) và (d2)
c) c/m(d1) vuông góc với (d2), Tính chu vi tam giác tạo bởi (d1), (d2) và trục Oy
Cho đường thẳng (d): y= (m-2)x+2m-3
a) vẽ đồ thị của hàm số khi m=1. Gọi đt đó là (d1)
b) Cho (d2): y= x-5. Tìm tọa độ giao điểm A của (d1) và (d2)
c) c/m(d1) vuông góc với (d2), Tính chu vi tam giác tạo bởi (d1), (d2) và trục Oy
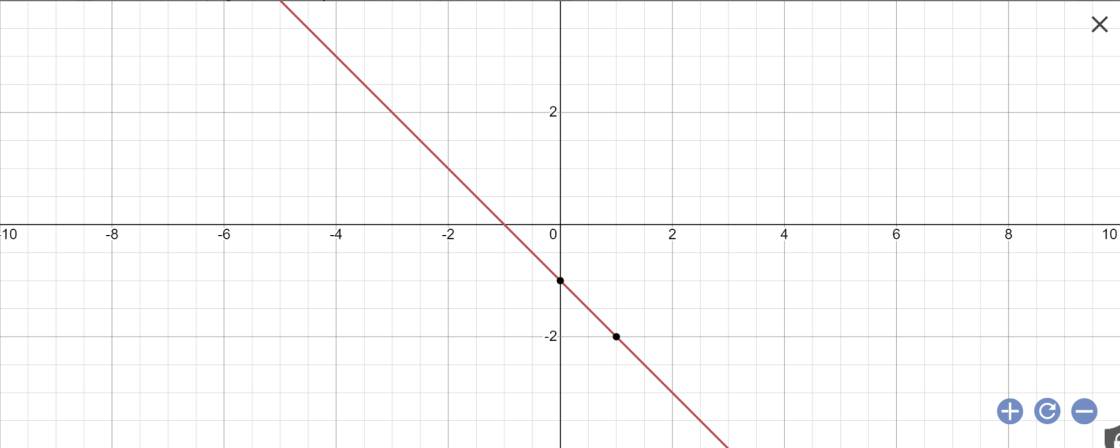
a: Khi m=1 thì y=(1-2)x+2*1-3
\(\Leftrightarrow y=-x-1\)
(d1): y=-x-1
b: Tọa độ A là nghiệm của hệ phương trình sau:
\(\left\{{}\begin{matrix}-x-1=x-5\\y=x-5\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}-2x=-4\\y=x-5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\y=2-5=-3\end{matrix}\right.\)
c: \(a_1\cdot a_2=1\cdot\left(-1\right)=-1\)
=>\(\left(d1\right)\perp\left(d2\right)\)
tìm m để 3 đt (d1) y=x+1, (d2) y= -x+m, (d3) y=3x đồng quy
cho hai đt (d): y=-2x+1
(d1) : y=x-1
a) vẽ đồ thị (d) và (d1) trên cùng mptđ
b) xác định tọa độ giao điểm A của 2 đt (d) và (D1) bằng phép toán
c) viết pt đường thẳng (d2): y=ax+b (\(a\ne0\)) song song với đt (D1) cắt trục hoành tại điểm có hoành độ bằng 2
a)( x= 0 ; y = 1); (y=0; x= 1/2) đt1
(x=0;y = -1) ; (y=0;x= 1) đt2
b) giao điểm tức là cùng nghiệm
-2x+1 = x- 1 => x = 2/3 ; y = -1/3
A(2/3; -1/3)
c) anh xem đk // là làm dc, em mệt r