Câu 10:
\(\dfrac{AB}{MK}=\dfrac{BC}{MN}=\dfrac{CA}{KN}\Rightarrow\Delta ABC\sim\Delta KMN\)
\(\rightarrow D\)
Câu 11:
AD là phân giác của tam giác ABC \(\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{CD}\Rightarrow\dfrac{AB}{BD}=\dfrac{AC}{BC-BD}\)
\(\Rightarrow\dfrac{8}{BD}=\dfrac{12}{10-BD}\Rightarrow80-8BD=12BD\Rightarrow BD=4\left(cm\right)\)
\(\rightarrow A\)
Câu 12:
Ta có: \(\Delta ABC\sim\Delta DEF\) theo hệ số \(k_1\) \(\Rightarrow\dfrac{AB}{DE}=k_1\)
\(AB=k_1\cdot DE\)
\(\Delta DEF\sim\Delta MNP\) theo hệ số \(k_2\) \(\Rightarrow\dfrac{DE}{MN}=k_2\)
\(MN=\dfrac{DE}{k_2}\)
Khi đó \(\Delta MNP\sim\Delta ABC\) theo hệ số: \(\dfrac{MN}{AB}=\dfrac{\dfrac{DE}{k_2}}{DE\cdot k_1}=\dfrac{\dfrac{1}{k^2}}{k_1}=\dfrac{1}{k_1\cdot k_2}\)
\(\rightarrow A\)






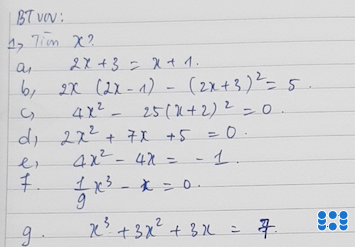
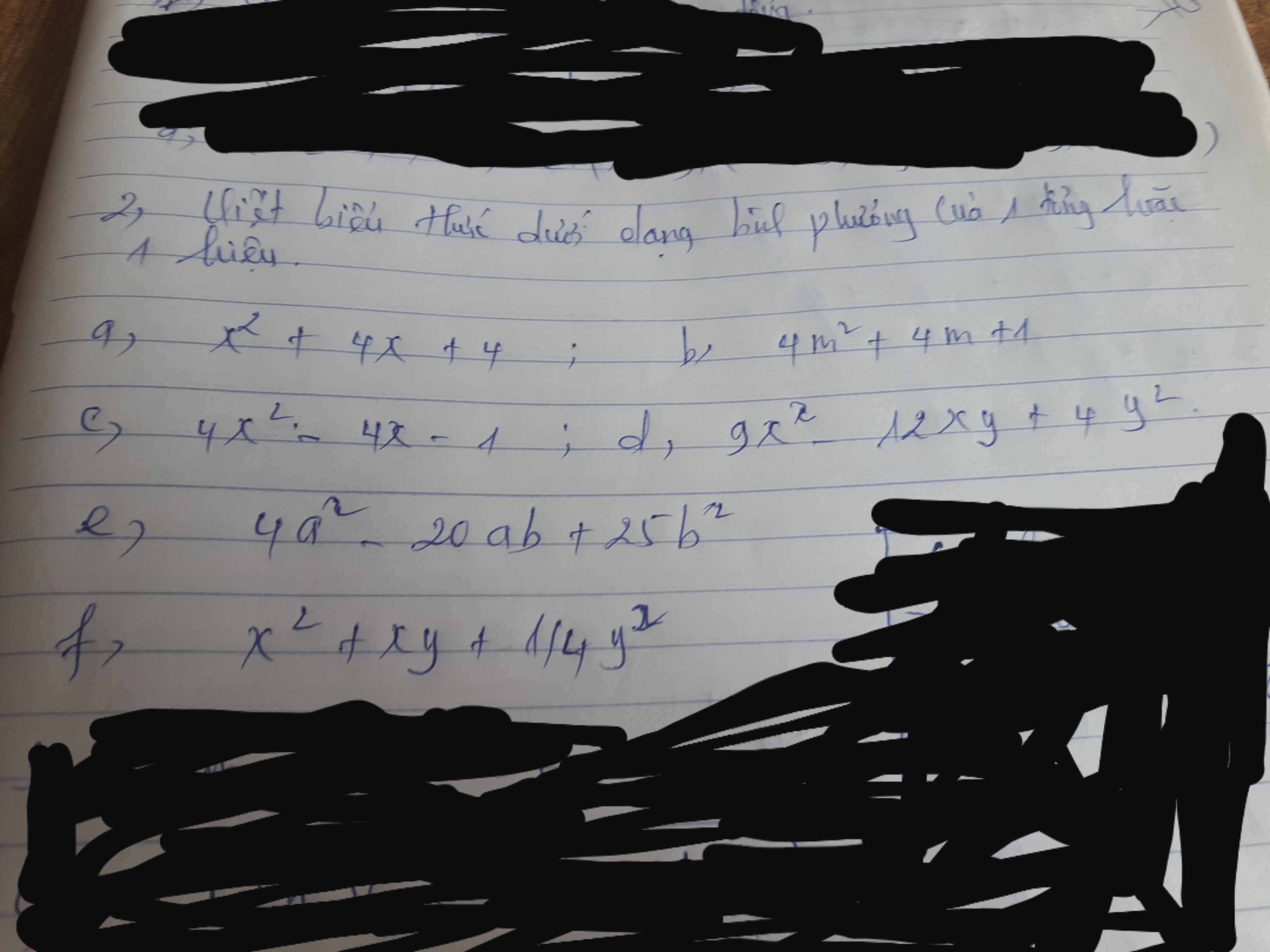

 giải thích giùm mình với
giải thích giùm mình với