Câu 15:
a: Xét ΔAOB và ΔCOD có
\(\widehat{AOB}=\widehat{COD}\)(hai góc đối đỉnh)
\(\widehat{OBA}=\widehat{ODC}\)(hai góc so le trong, BA//CD)
Do đó: ΔAOB~ΔCOD
b: Xét ΔKDH có AE//DH
nên \(\dfrac{AE}{DH}=\dfrac{KE}{KH}=\dfrac{KA}{KD}\left(1\right)\)
Xét ΔKHC có EB//HC
nên \(\dfrac{EB}{HC}=\dfrac{KE}{KH}\left(2\right)\)
Từ (1),(2) suy ra \(\dfrac{AE}{DH}=\dfrac{EB}{HC}\)
=>\(AE\cdot HC=EB\cdot HD\)
c: Xét ΔOAE và ΔOCH có
\(\widehat{OAE}=\widehat{OCH}\)(hai góc so le trong, AE//CH)
\(\widehat{AOE}=\widehat{COH}\)(hai góc đối đỉnh)
Do đó: ΔOAE~ΔOCH
=>\(\dfrac{AE}{CH}=\dfrac{OA}{OC}\left(3\right)\)
Ta có: ΔAOB~ΔCOD
=>\(\dfrac{OA}{OC}=\dfrac{AB}{CD}\left(4\right)\)
Xét ΔKDC có AB//CD
nên \(\dfrac{AB}{CD}=\dfrac{KA}{KD}\left(5\right)\)
Từ (1),(3),(4),(5) suy ra \(\dfrac{AE}{CH}=\dfrac{AE}{DH}\)
=>CH=DH
=>H là trung điểm của CD
Ta có: \(\dfrac{AE}{DH}=\dfrac{EB}{HC}\)
mà HD=HC
nên AE=EB
=>E là trung điểm của AB
=>\(\dfrac{AE}{AB}=\dfrac{1}{2}\)
Câu 13:







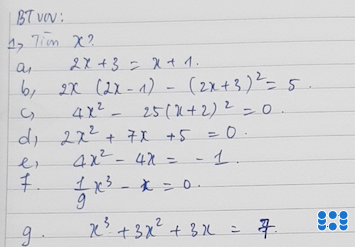
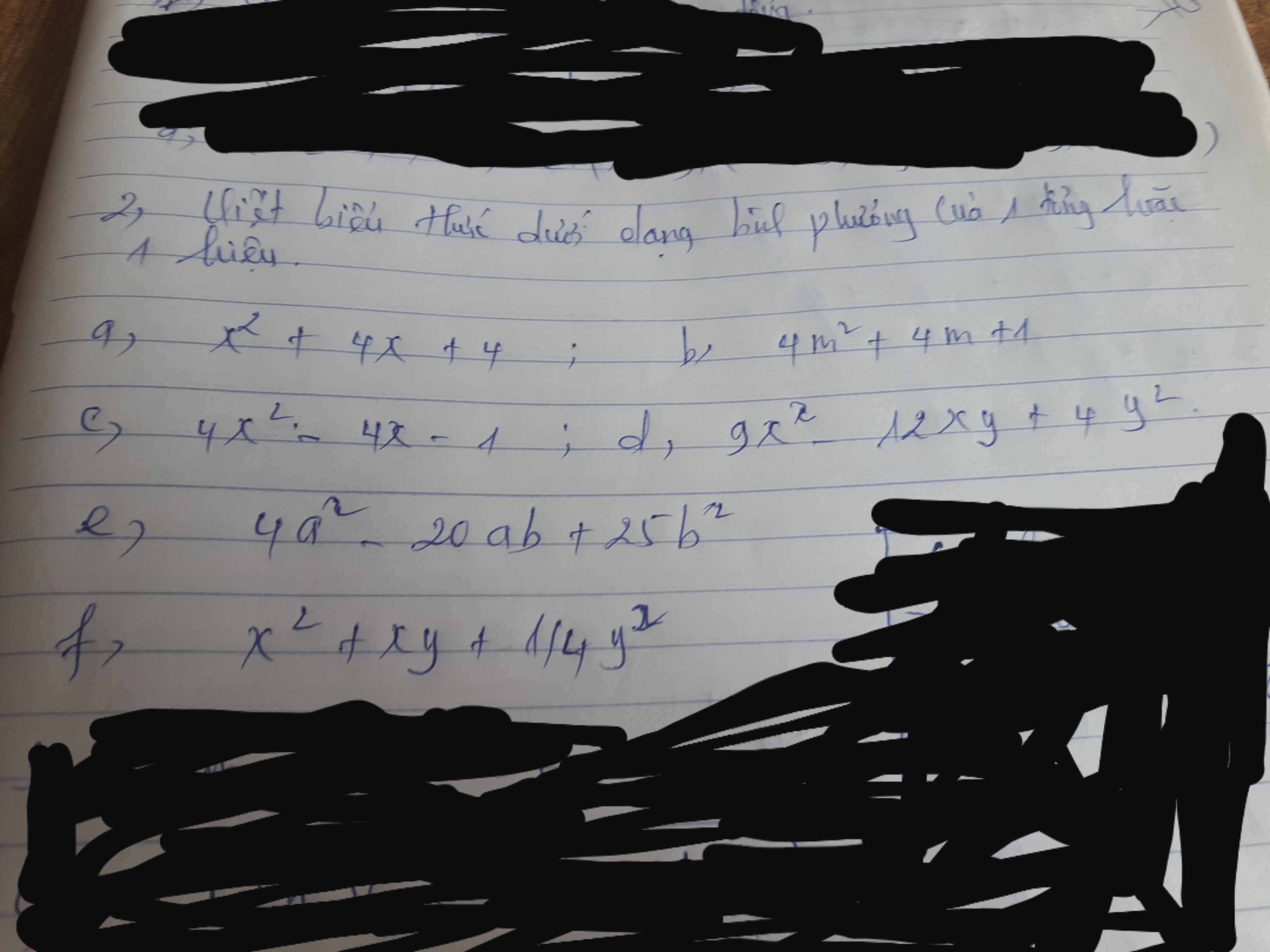

 giải thích giùm mình với
giải thích giùm mình với