Bài 16:
Ta có:
\(Q=\dfrac{5x^2-24x+29}{x^2-4x+4}\left(x\ne2\right)\)
\(Q=\dfrac{x^2-4x+4+4x^2-20x+25}{x^2-4x+4}\)
\(Q=\dfrac{x^2-4x+4}{x^2-4x+4}+\dfrac{4x^2-20x+25}{x^2-4x+4}\)
\(Q=1+\dfrac{\left(2x\right)^2-2\cdot2x\cdot5+5^2}{x^2-2\cdot x\cdot2+2^2}\)
\(Q=1+\dfrac{\left(2x-5\right)^2}{\left(x-2\right)^2}\)
Mà: \(\dfrac{\left(2x-5\right)^2}{\left(x-2\right)^2}\ge0\forall x\ne2\)
\(\Rightarrow Q=1+\dfrac{\left(2x-5\right)^2}{\left(x-2\right)^2}\ge1\forall x\ne2\)
Dấu "=" xảy ra: \(\left(2x-5\right)^2=0\Leftrightarrow2x-5=0\Leftrightarrow x=\dfrac{5}{2}\left(tm\right)\)
Vậy: \(Q_{min}=1\Leftrightarrow x=\dfrac{5}{2}\)
Câu 14:
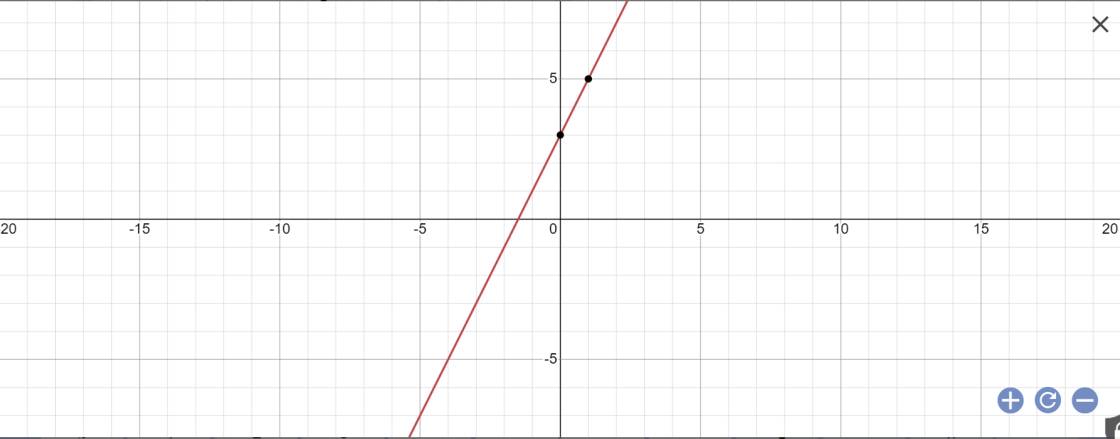
a: Thay x=2 và y=7 vào y=2x+b, ta được:
\(b+2\cdot2=7\)
=>b+4=7
=>b=3
=>y=2x+3
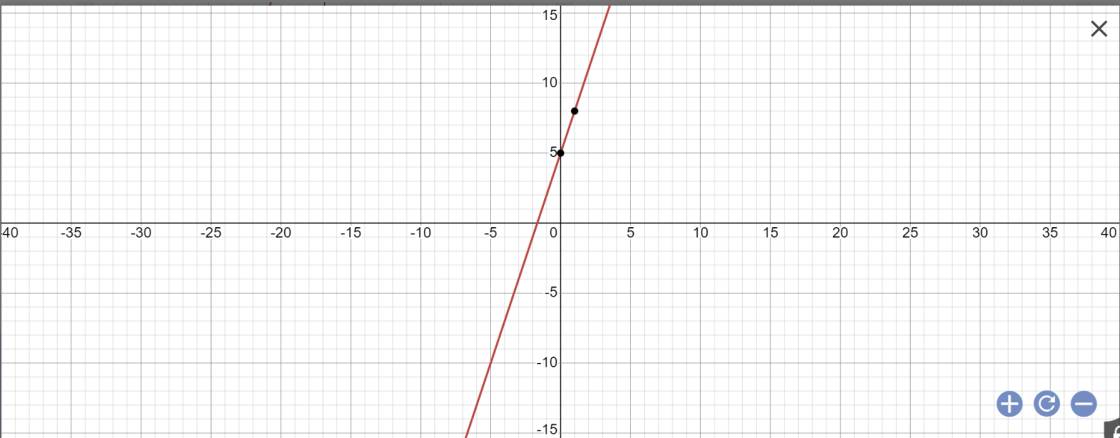
b: Thay x=-2 và y=-1 vào y=ax+5, ta được:
-2a+5=-1
=>-2a=-6
=>a=3
=>y=3x+5
Câu 15:
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: Xét ΔHBA vuông tại H và ΔHAC vuông tại H có
\(\widehat{HBA}=\widehat{HAC}\left(=90^0-\widehat{HAB}\right)\)
Do đó: ΔHBA~ΔHAC
=>\(\dfrac{HB}{HA}=\dfrac{HA}{HC}\)
=>\(HA^2=HB\cdot HC\)
c:
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH^2=4\cdot16=64\)
=>\(AH=\sqrt{64}=8\left(cm\right)\)
Xét tứ giác ADHE có \(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
nên ADHE là hình chữ nhật
=>AH=DE
mà AH=8cm
nên DE=8cm
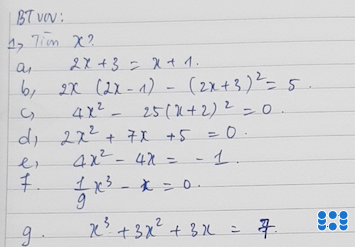
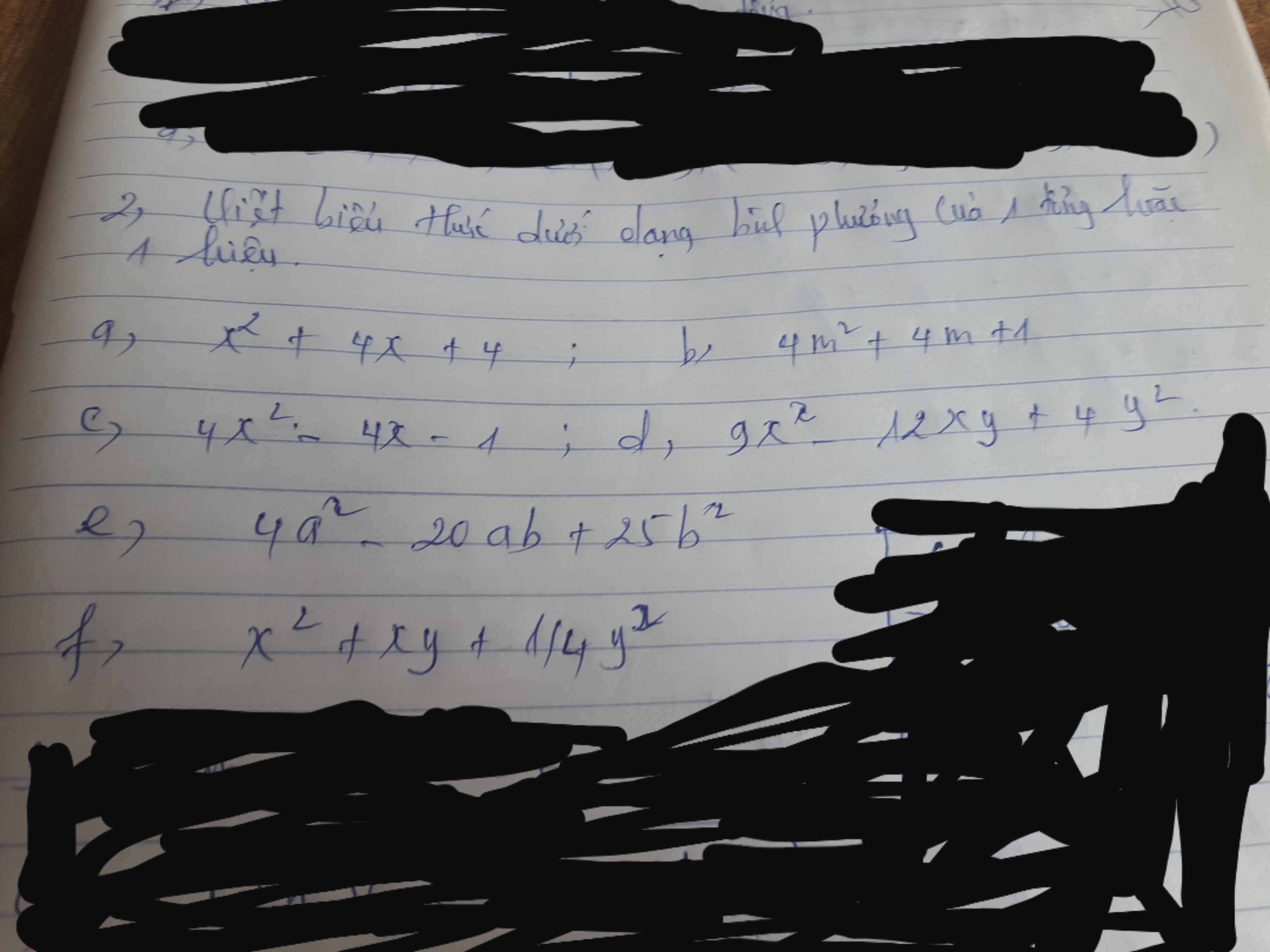
giải thích giùm mình với