Câu 14:
a: Hệ số góc bằng -3 nên a=-3
=>y=-3x+b
Thay x=1 và y=3 vào y=-3x+b, ta được:
\(-3\cdot1+b=3\)
=>b-3=3
=>b=6
Vậy: y=-3x+6
b: Vì đồ thị hàm số y=ax+b song song với đường thẳng y=4x-1 nên \(\left\{{}\begin{matrix}a=4\\b\ne-1\end{matrix}\right.\)
Vậy: y=4x+b
Thay x=-1 và y=4 vào y=4x+b, ta được:
\(4\cdot\left(-1\right)+b=4\)
=>b-4=4
=>b=8
Vậy: y=4x+8
Câu 15:
a: Xét ΔCHM vuông tại H và ΔCDA vuông tại D có
\(\widehat{HCM}\) chung
Do đó: ΔCHM~ΔCDA
b: Xét ΔHCB vuông tại H và ΔBCA vuông tại B có
\(\widehat{HCB}\) chung
Do đó: ΔHCB~ΔBCA
=>\(\dfrac{HC}{BC}=\dfrac{BC}{CA}\)
=>\(BC^2=CH\cdot CA\left(1\right)\)
Ta có: ΔCMH~ΔCAD
=>\(\dfrac{CM}{CA}=\dfrac{CH}{CD}\)
=>\(CH\cdot CA=CM\cdot CD\left(2\right)\)
Từ (1),(2) suy ra \(CM\cdot CD=BC^2\)
=>\(MC=\dfrac{BC^2}{CD}=\dfrac{6^2}{8}=4,5\left(cm\right)\)






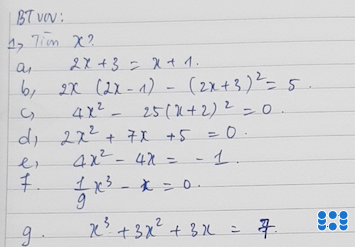
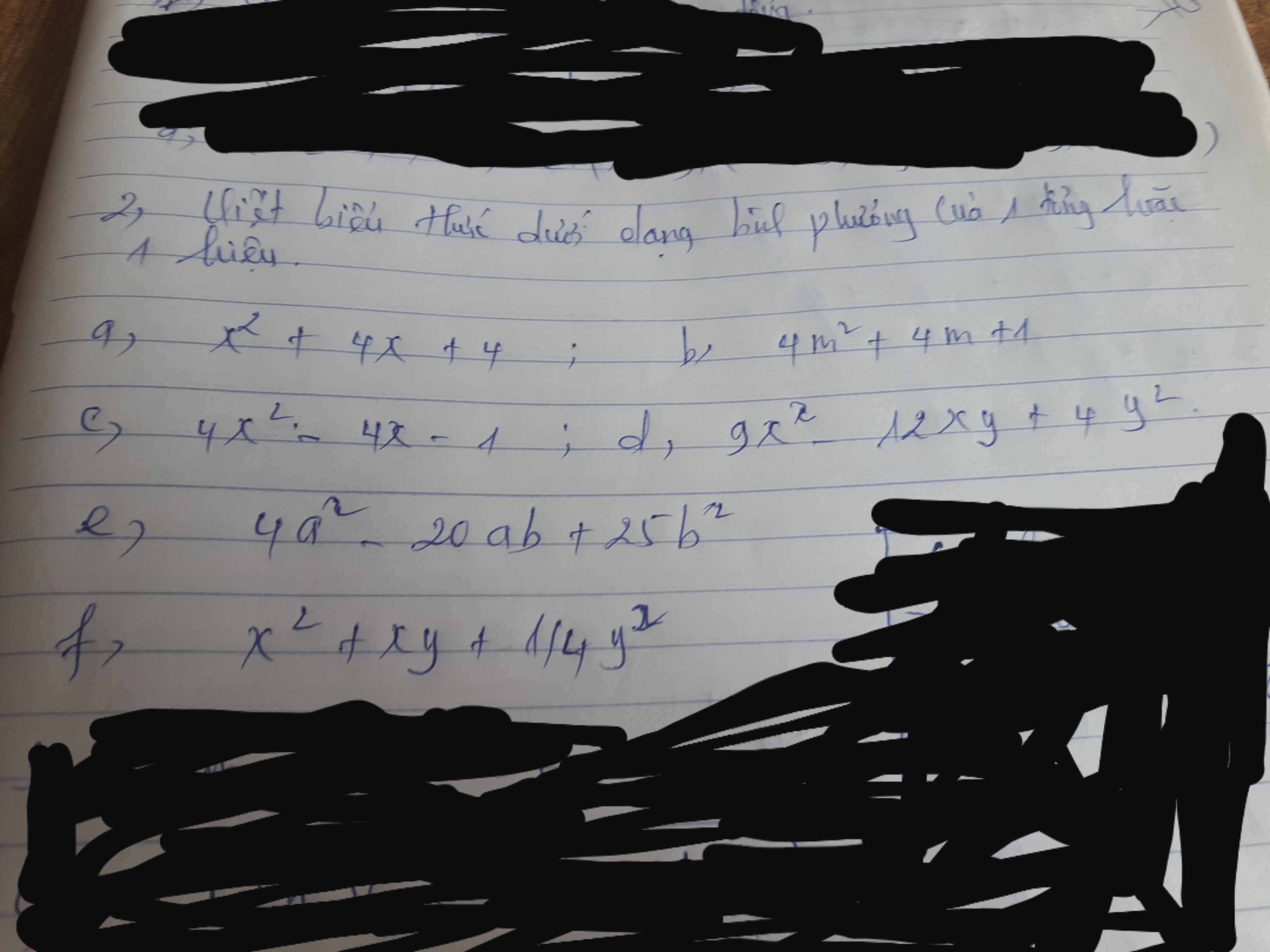

 giải thích giùm mình với
giải thích giùm mình với